
Enhetlig rätlinjig rörelseegenskap, formler, övningar
De enhetlig linje rörelse eller med konstant hastighet är en i vilken partikeln rör sig längs en rak linje och med konstant hastighet. På detta sätt färdas mobilen lika långa sträckor på lika tid. Till exempel, om du på 1 sekund reser 2 meter, efter 2 sekunder har du rest 4 meter och så vidare.
För att göra en korrekt beskrivning av rörelsen, vare sig det är enhetligt rätlinjigt eller annat, är det nödvändigt att upprätta en referenspunkt, även kallad källa, med avseende på vilken mobilen byter position.

Om rörelsen löper helt längs en rak linje är det också viktigt att veta i vilken riktning den rörliga kroppen färdas.
På en horisontell linje är det möjligt att mobilen går åt höger eller vänster. Skillnaden mellan båda situationerna görs med tecken, den vanliga konventionen är följande: till höger följer jag (+) och till vänster undertecknar jag (-).
När hastigheten är konstant ändrar inte mobilen sin riktning eller sin känsla, och dessutom förblir dess hastighet oförändrad..
Artikelindex
- 1 Funktioner
- 1.1 Avstånd från v vs. diagram t
- 2 Formler och ekvationer
- 3 Lösta övningar
- 3.1 Löst övning 1
- 3.2 -Löst övning 2
- 4 applikationer
- 5 Referenser
Egenskaper
Huvudegenskaperna för den enhetliga rätlinjiga rörelsen (MRU) är följande:
-Rörelsen går alltid längs en rak linje.
-En mobil med MRU färdas lika långa avstånd eller mellanslag i lika stora tider.
-Hastigheten förblir oförändrad både i storlek och i riktning och känsla.
-MRU saknar acceleration (ingen hastighetsförändring).
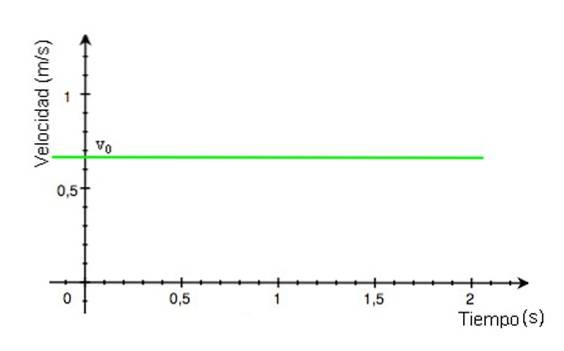
-Sedan hastigheten v förblir konstant över tiden t, diagrammets storlek som funktion av tiden är en rak linje. I exemplet i figur 2 är linjen färgad grön och hastighetsvärdet avläses på den vertikala axeln, ungefär +0,68 m / s.
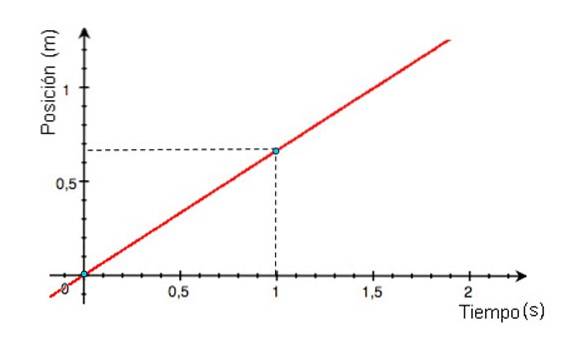
-Grafen för positionen x med avseende på tid är en rak linje vars lutning är lika med mobilens hastighet. Om linjen i diagrammet x vs t är horisontell är mobilen i vila, om lutningen är positiv (grafen i figur 3) är hastigheten också positiv.
Avstånd som rest från v vs. diagram. t
Känn avståndet som mobilen har rest när v vs. grafen är tillgänglig. t är väldigt enkelt. Avståndet är lika med området under linjen och inom det önskade tidsintervallet.
Antag att du vill veta avståndet med mobilen i figur 2 i intervallet mellan 0,5 och 1,5 sekunder.
Detta område är det för den skuggade rektangeln i figur 4. Det beräknas genom att hitta resultatet av att multiplicera rektangelns bas med dess höjd, vars värden avläses från diagrammet.
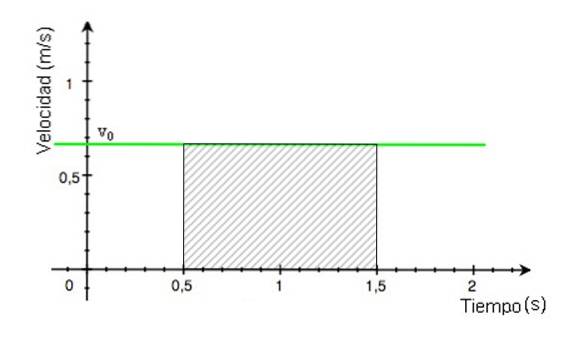
Resad sträcka = (1,5 - 0,5) x 0,68 m = 0,68 m
Avstånd är alltid en positiv kvantitet, oavsett om det går åt höger eller vänster..
Formler och ekvationer
I MRU är medelhastigheten och den momentana hastigheten alltid desamma och eftersom deras värde är lutningen på diagrammet x vs t motsvarande en linje, är motsvarande ekvationer som en funktion av tiden följande:
-Position som en funktion av tiden: x (t) = xeller + vt
xeller representerar mobilens initialposition, vid många tillfällen sammanfaller den med referenssystemets ursprung, men så är inte alltid fallet. Denna ekvation är också känd som resväg ekvation.
-Hastighet som en funktion av tiden: v (t) = konstant
När v = 0 betyder det att mobilen är i vila. Vila är ett särskilt fall av rörelse.
-Acceleration som en funktion av tiden: a (t) = 0
Vid enhetlig rätlinjig rörelse sker inga hastighetsförändringar, därför är accelerationen noll.
Lösta övningar
När du löser en övning, se till att situationen motsvarar den modell som ska användas. Framför allt är det nödvändigt att se till att de är tillämpliga innan du använder MRU-ekvationerna.
Följande lösta övningar är problem med två mobiler.
Löst övning 1
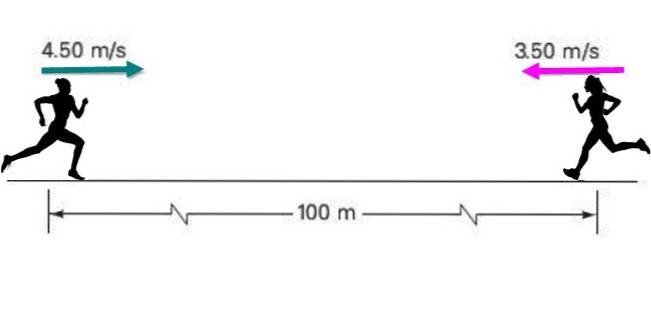
Två idrottare närmar sig varandra med en konstant hastighet på 4,50 m / s respektive 3,5 m / s, inledningsvis åtskilda med ett avstånd på 100 meter, som anges i figuren.
Om var och en håller sin hastighet konstant, hitta: a) Hur lång tid tar de att träffas? b) Vilken ställning kommer var och en vid den tiden?
Lösning
Det första är att ange ursprunget till det koordinatsystem som ska fungera som referens. Valet beror på vilken person som löser problemet..
Vanligtvis väljs x = 0 direkt vid mobilens startpunkt, det kan vara i vänster eller höger korridor, det kan till och med väljas i mitten av båda.
a) Vi ska välja x = 0 på vänster löpare eller löpare 1, därför är startpositionen för detta x01 = 0 och för löpare 2 blir det x02 = 100 m. Löpare 1 rör sig från vänster till höger med hastighet v1 = 4,50 m / medan löpare 2 gör det från höger till vänster med en hastighet på -3,50 m / s.
Rörelseekvation för den första löparen
x1 = x01 + v1t1 = 4,50 ton1
Rörelseekvation för den andra löparen
xtvå = x02 + vtvåttvå = 100 -3,50ttvå
Eftersom tiden är densamma för båda t1 = ttvå = t , när de möter båda ställning kommer att vara densamma, därför x1 = xtvå. Motsvarande:
4,50 ton = 100 -3,50 ton
Det är en ekvation av första graden för tid, vars lösning är t = 12,5 s.
b) Båda löparna är i samma position, därför ersätter detta den tid som erhölls i föregående avsnitt i någon av positionsekvationerna. Till exempel kan vi använda mäklare 1:
x1 = 4,50 ton1 = 56,25 m
Samma resultat uppnås genom att ersätta t = 12,5 s i positionsekvationen för löpare 2.
-Övning löst 2
Haren utmanar sköldpaddan att springa ett avstånd på 2,4 km och att vara rättvis ger honom en halvtimme försprång. I spelet rör sig sköldpaddan med en hastighet på 0,25 m / s, vilket är det maximala den kan springa. Efter 30 minuter springer haren vid 2 m / s och tar snabbt upp sköldpaddan.
Efter att ha fortsatt i ytterligare 15 minuter tror hon att hon har tid att ta sig en tupplur och ändå vinna loppet, men somnar i 111 minuter. När han vaknar springer han med all sin kraft, men sköldpaddan korsade redan mållinjen. Hitta:
a) Med vilken fördel vinner sköldpaddan?
b) Det ögonblick då haren passerar sköldpaddan
c) Det ögonblick då sköldpaddan överträffar haren.
Lösning till)
Loppet börjar om t = 0. Sköldpaddans position: xT = 0,25 ton
Harrörelsen har följande delar:
-Vila för den fördel det gav sköldpaddan: 0 < t < 30 minutos:
-Tävla för att komma ikapp med sköldpaddan och fortsätt springa lite efter att ha passerat den; totalt finns det 15 minuters rörelse.
-Sov i 111 minuter (vila)
-Vakna för sentsprinta slutlig)
2,4 km = 2400 m
Loppet varade: t = 2400 m / 0,25 m / s = 9600 s = 160 min. Från den här tiden tar vi 111 minuter från tupplur och 30 minuter framåt, vilket gör 19 minuter (1140 sekunder). Det betyder att du sprang i 15 minuter innan du somnade och 4 minuter efter att du vaknat för sprinten.
Under den här tiden täckte haren följande avstånd:
dL = 2 m / s. (15. 60 s) + 2 m / s (4. 60 s) = 1800 m + 480 m = 2280 m.
Eftersom det totala avståndet var 2400 meter, och båda värdena subtraherades, visar det sig att haren var 120 meter från att nå målet..
Lösning b)
Harens position innan den somnar är xL = 2 (t - 1800), med tanke på fördröjningen på 30 minuter = 1800 sekunder. Matchande xT och xL vi hittar den tid då de är:
2 (t - 1800) = 0,25 ton
2t -0,25 t = 3600
t = 2057,14 s = 34,29 min
Lösning c)
När haran överkörs av sköldpaddan sover den 1800 meter från början:
1800 = 0,25 ton
t = 7200 s = 120 min
Applikationer
MRU är den enklaste rörelsen som kan föreställas och det är därför den är den första som studeras inom kinematik, men många komplexa rörelser kan beskrivas som en kombination av denna och andra enkla rörelser..
Om en person lämnar sitt hus och kör tills han når en lång rak motorväg längs vilken han färdas med samma hastighet under lång tid, kan hans rörelse globalt beskrivas som en MRU, utan att gå mer i detalj.
Naturligtvis måste personen ta några varv innan han går in och ut på motorvägen, men genom att använda denna rörelsemodell kan resans längd beräknas med vetskap om det ungefärliga avståndet mellan startpunkten och ankomstpunkten..
I naturen har ljus en enhetlig rätlinjig rörelse vars hastighet är 300.000 km / s. På samma sätt kan ljudets rörelse i luften antas vara enhetlig rätlinjig med en hastighet på 340 m / s i många applikationer..
När man analyserar andra problem, till exempel rörelse av laddningsbärare inuti en ledningstråd, kan MRU-approximationen också användas för att ge en uppfattning om vad som händer inuti ledaren..
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 40-45.
- Figueroa, D. Physics Series for Sciences and Engineering. Volym 3: e. Utgåva. Kinematik. 69-85.
- Giancoli, D. Fysik: Principer med tillämpningar. 6th. Ed Prentice Hall. 19-36.
- Hewitt, Paul. 2012. Konceptuell fysik. 5th. Ed Pearson. 14-18.
- Kirkpatrick, L. 2007. Fysik: En titt på världen. 6ta Förkortad upplaga. Cengage Learning. 15-19.
- Wilson, J. 2011. Fysik 10. Pearson Education. 116-119.



Ingen har kommenterat den här artikeln än.