Relativ rörelse i en dimension, i två dimensioner, övningar

De relativ rörelse av en partikel eller ett objekt är den som observeras med avseende på en viss referenspunkt som observatören har valt, vilken kan fixeras eller i rörelse. Hastighet refererar alltid till något koordinatsystem som används för att beskriva det.

Till exempel är passageraren i en bil i rörelse och som sover bekvämt i sitt säte i vila i förhållande till föraren, men inte för en observatör som står på trottoaren och ser bilen gå förbi..

Då är rörelsen alltid relativ, men det händer att i allmänhet koordinat- eller referenssystemet väljs med sitt ursprung i jorden eller marken, en plats som anses vara stillastående. På detta sätt fokuserar man på att beskriva rörelsen för det objekt som studeras..

Är det möjligt att beskriva hastigheten på den sovande piloten jämfört med en passagerare som reser i en annan bil? Svaret är ja. Det finns frihet att välja värdet på (x_eller, Y_eller, z_eller): referenssystemets ursprung. Valet är godtyckligt och beror på observatörens preferenser, liksom på hur lätt det är att lösa problemet..

Artikelindex

• 1 Relativ rörelse i en dimension
  • 1.1 - Fungerat exempel 1
• 2 Relativ rörelse i två och tre dimensioner
  • 2.1 -Löst övning 2 
  • 2.2 -Löst övning 3
• 3 Referenser

Relativ rörelse i en dimension

När rörelsen sker längs en rak linje har mobilerna hastigheter i samma riktning eller i motsatt riktning, båda sett av en observatör som står på jorden (T). Rör sig observatören med avseende på mobilerna? Ja, med samma hastighet som de bär, men i motsatt riktning.

Hur rör sig den ena mobilen i förhållande till den andra? För att ta reda på läggs hastigheterna till vektorellt.

-Fungerat exempel 1

Med hänvisning till den visade figuren, ange den relativa hastigheten för bil 1 i förhållande till bil 2 i varje situation.

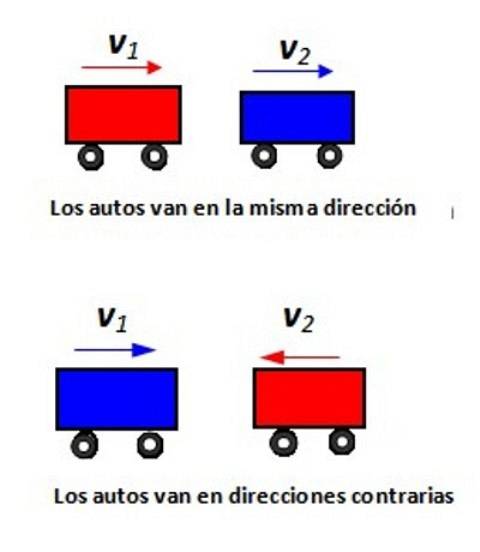
Lösning

Vi kommer att tilldela ett positivt tecken till hastigheterna till höger och ett negativt tecken till vänster. Om en mobil går till höger i 80 km / h ser en passagerare på den här mobilen observatören på jorden röra sig i - 80 km / h.

Antag att allt händer längs x-axeln. I följande bild rör sig den röda bilen i +100 km / h (sett från T) och är på väg att passera den blå bilen som kör +80 km / h (sett också från T). Hur snabbt närmar sig en passagerare i den blå bilen den röda bilen?

Etiketterna är: v _1/2 hastighet på bil 1 i förhållande till bil 2, v_{1 / T.} bilens hastighet med avseende på T, v_{T / 2} hastighet av T med avseende på 2. Vektortillägg:

v_1/2 = v_{1 / T.} + v_{T / 2} = (+100 km / h - 80 km / h) x= 20 km / h x

Vi kan klara oss utan vektornotationen. Lägg märke till prenumerationerna: multiplicera de två till höger så ska du få den till vänster.

Och när de går åt andra hållet? Nu v_{1 / T.} = + 80 km / h och v_{2 / T.} = -100 km / h, därför v_{T / 2} = + 100 km / h. Passageraren i den blå bilen ser den röda bilen närma sig:

v_{1/2 =} v_{1 / T.} + v_{T / 2} = +80 km / h +100 km / h = 180 km / h

Relativ rörelse i två och tre dimensioner

I följande schema, r är planet för planet sett från systemet X och Z, rär positionen från systemet X och Z ' Y R är systemets position med en premie i förhållande till systemet utan premie. De tre vektorerna bildar en triangel i vilken R + r'= r, Således r'= r - R.

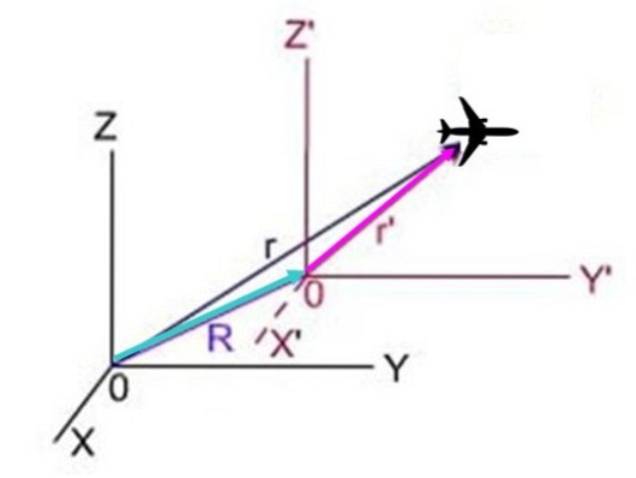
Eftersom derivatet med avseende på positionstid är exakt hastigheten, resulterar det:

v'= v - eller

I denna ekvation v'är planets hastighet i förhållande till systemet X och Z ', v är hastigheten i förhållande till systemet X och Z Y eller är den primära systemets konstanta hastighet med avseende på det icke-primade systemet.

-Övning löst 2 

Ett flygplan är på väg norrut med en flyghastighet på 240 km / h. Plötsligt börjar vinden blåsa från väst till öst med en hastighet på 120 km / beroende på jorden.

Hitta: a) Planets hastighet i förhållande till marken, b) Pilotens avvikelse c) Den korrigering som piloten måste göra för att kunna sikta direkt norrut och den nya hastigheten i förhållande till marken, en gång korrigeringen har gjorts.

Lösning

a) Det finns följande element: plan (A), mark (T) och vind (V).

I koordinatsystemet i vilket norr är + y-riktningen och väst-östlig riktning är + x, har vi de angivna hastigheterna och deras respektive etikett (abonnemang):

v _AV = 240 km / h (+Y); v _{V / T} = 120 km / h (+x); v _{A / T} = ?

Den rätta vektorsumman är:

v _{A / T} = v _AV + v _{V / T} = 240 km / h (+Y) + 120 km / h (+x)

Storleken på denna vektor är: v _{A / T} = (240 ^två+ 120^två)^1/2 km / h = 268,3 km / h

b) θ = arctg (v _AV / v _{V / T}) = arctg (240/120) = 63,4 º norr om öst eller 26,6 º nordost.

c) För att fortsätta norrut med denna vind måste du rikta flygplanets båge mot nordväst så att vinden driver dig direkt norrut. I detta fall kommer planetens hastighet sett från marken att vara i + y-riktningen, medan planetens hastighet i förhållande till vinden kommer att vara nordväst (det behöver inte nödvändigtvis vara 26,6º).

Av Pythagoras sats:

v _{A / T} = (240 ^två- 120^två)^1/2 km / h = 207,8 km / h

α = arctg (v _{V / T} / v _{A / T} ) = arctg (120 / 207.8) = 30º nordväst

-Övning löst 3

Det tar en person 2 minuter att gå nerför en stillastående rulltrappa. Om stegen fungerar tar det personen 1 minut att gå ner medan han står stilla. Hur lång tid tar det för personen att gå ner med stegen i gång?

Lösning

Det finns tre element att tänka på: personen (P), stegen (E) och marken (S), vars relativa hastigheter är:

v_{P / E} : personens hastighet med avseende på stegen; v_{DET ÄR}: stegehastighet i förhållande till marken; v_{P / S}: personens hastighet i förhållande till marken.

Sett från marken av en fast observatör har personen som stiger nedför stegen (E) en hastighet v _{P / S} getts av:

v _{P / S} = v_{P / E} + v_{DET ÄR}

Den positiva riktningen går nerför stegen. Vara t  den tid det tar att gå ner och L distans. Storleken på personens hastighet v _{P / S} det är:

v_{P / S} = L / t

t₁ är tiden det tar att gå ner med stegen stängd: v _{P / E} = L / t₁

Och t_två den som tar dig ner stilla på den rörliga trappan: v _{DET ÄR} = L / t_två

Kombinera uttrycken:

L / t = L / t₁ + L / t_två

Ersätta numeriska värden och lösa t:

1 / t = 1 / t₁ + 1 / t_två = 1/2 + 1/1 = 1,5

Så t = 1 / 1,5 minuter = 40 sekunder.

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volym 3: e. Utgåva. Kinematik. 199-232.
3. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6^th. Ed Prentice Hall. 62-64.
4. Relativ rörelse. Återställd från: courses.lumenlearning.com
5. Wilson, J. 2011. Fysik 10. Pearson Education. 166-168.