Vinklar i omkretsstyper, egenskaper, lösta övningar

Kallad omkretsvinklar de där några av dess element är eller skär varandra vid en given omkrets. Bland dem är följande:

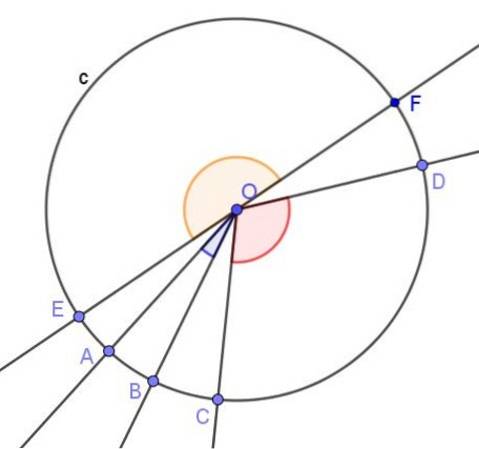
1.- central vinkel, vars topp är i mitten av omkretsen och dess sidor är sekant för det, som vi ser i följande bild:

2.- inskriven vinkel, vars topp är på omkretsen och dess sidor är avskilda eller tangent till omkretsen.

3.- Utvändig vinkel, vars topp är utanför omkretsen men dess sidor är avskilda eller tangent till omkretsen.

4.- inre vinkel, med toppunkten inuti omkretsen och dess sidor avskilda från den.

Alla dessa vinklar har vissa relationer med varandra och detta leder oss till viktiga egenskaper mellan vinklarna som tillhör en given cirkel.

Artikelindex

• 1 Fastigheter
  • 1.1 - Central vinkel
  • 1.2 - Inskriven vinkel
  • 1.3 - Utvändig vinkel
  • 1.4 - Inre vinkel
• 2 Lösta övningar
  • 2.1 - Övning 1
  • 2.2 - Övning 2
• 3 Referenser

Egenskaper

- Central vinkel

Den centrala vinkeln definieras som den vars topp är i centrum av omkretsen och dess sidor skär varandra.

Måttet i radianer av en central vinkel är kvoten mellan den nedåtgående bågen, det vill säga bågen för omkretsen mellan sidorna av vinkeln och radien för omkretsen. 

Om omkretsen är enhetlig, det vill säga av radie 1, är måttet på den centrala vinkeln längden på bågen, vilket motsvarar antalet radianer.

Om du vill mäta den centrala vinkeln i grader, multiplicera sedan måttet i radianer med faktorn 180º / π.

Vinkelmätinstrument, som gradskiva och goniometer, använder alltid en central vinkel och längden på den nedsänkta bågen.

De är kalibrerade i sexagesimala grader, vilket innebär att när en vinkel mäts med dem, i bakgrunden är vad som mäts längden på bågen som är nedtryckt av den centrala vinkeln.

Fast egendom

Måttet på en central vinkel i radianer är lika med längden på den utskjutande eller avlyssningsbågen dividerad med radiens längd.

- Inskriven vinkel

Den inskrivna vinkeln för en cirkel är en som har sin topp på omkretsen och dess strålar är sekant eller tangent till den.. 

Dess egenskaper är:

Egenskaper

-Den inskrivna vinkeln är konvex eller plan.

-När en inskriven vinkel skär samma båge som den centrala vinkeln, kommer måttet på den första vinkeln att vara hälften av den andra..

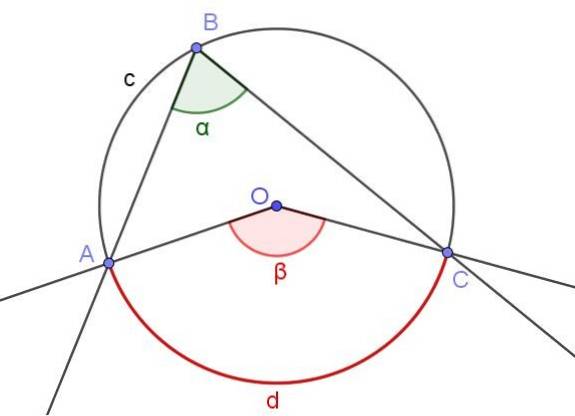
Figur 3 visar två vinklar ∠ABC och ∠AOC som korsar samma båge med omkrets A⌒C.

Om måttet på den inskrivna vinkeln är α, är måttet β för den centrala vinkeln dubbelt så stort som det inskrivna vinkeln (β = 2 α) eftersom båda täcker samma måttbåge d.

- Utvändig vinkel

Det är vinkeln vars topp ligger utanför omkretsen och var och en av dess sidor skär omkretsen på en eller flera punkter.

Fast egendom

-Dess mått är lika med halvskillnaden (eller skillnaden dividerad med 2) för de centrala vinklarna som fångar upp samma bågar.

För att säkerställa att mätningen är positiv måste halvskillnaden alltid vara den för den största centrala vinkeln minus måttet för den minsta centrala vinkeln, som illustreras i följande bild.

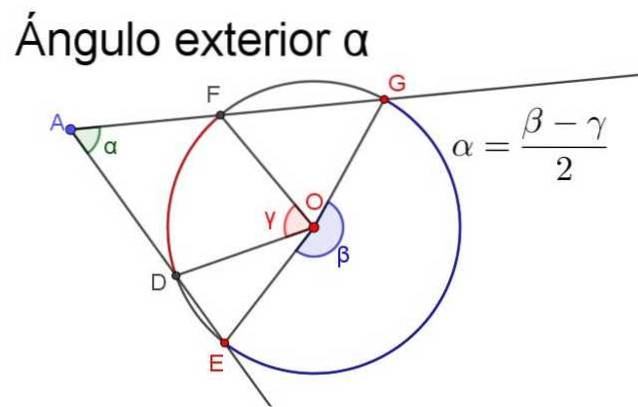
- Inre vinkel

Den inre vinkeln är den vars topp är inne i omkretsen och dess sidor skär varandra.

Fast egendom 

Dess mått är lika med halva summan av den centrala vinkeln som täcker samma båge, plus den centrala vinkeln som täcker samma båge som dess förlängningsvinkel (detta är den inre vinkeln som bildas av strålarna som är komplementära till den ursprungliga inre vinkel ).

Följande bild illustrerar och klargör egenskaperna för den inre vinkeln.

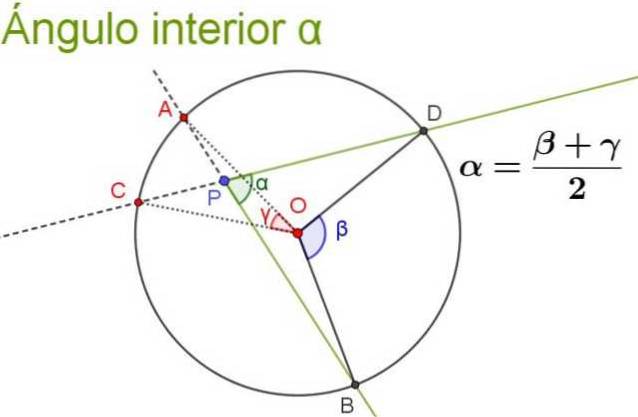
Lösta övningar

- Övning 1

Anta en inskriven vinkel i vilken en av dess sidor passerar genom cirkelns centrum, såsom visas i figur 6. Cirkelns radie är OA = 3 cm och bågen d har en längd på π / 2 cm. Bestäm värdet på vinklarna α och β.

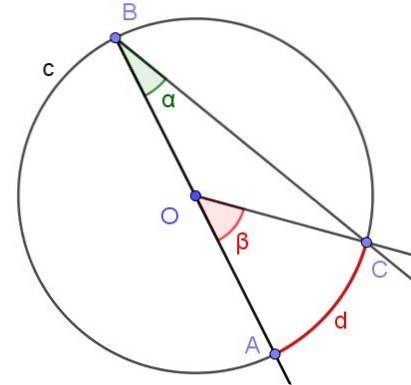
Lösning

I detta fall bildas den likbeniga triangeln COB, eftersom [OC] = [OB]. I en jämn triangel är vinklarna intill basen lika, därför är ∠BCO = ∠ABC = α. Å andra sidan ∠COB = 180º - β. Med tanke på summan av de inre vinklarna i triangeln COB har vi:

α + α + (180º - β) = 180º

Därav följer att 2 α = β, eller vad som är ekvivalent α = β / 2, med vilket egenskapen (3) i föregående avsnitt bekräftas, att måttet på den inskrivna vinkeln är halva den centrala vinkeln, när båda vinklarna undertrycka samma ackord [AC].

Nu fortsätter vi med att bestämma de numeriska värdena: vinkeln β är central och dess mått i radianer är kvoten mellan bågen d och radien r = OA, så dess mått är:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 º.

Å andra sidan hade det redan angetts att α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Övning 2

I figur 7 är vinklarna α₁ och β_två de har samma mått. Dessutom vinkeln β₁ mäter 60º. Bestäm vinklarna β och α.

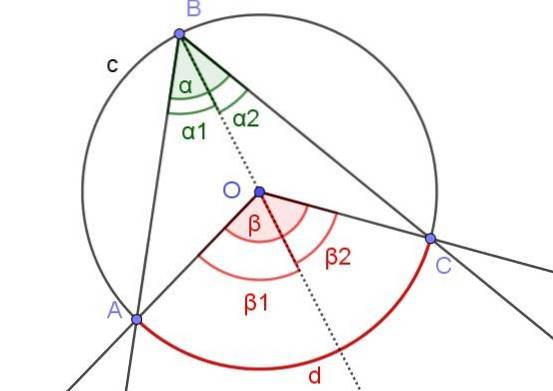
Lösning

I det här fallet har vi en inskriven vinkel ∠ABC där centrum O för omkretsen ligger inom vinkeln.

På grund av egenskapen (3) har vi α_två = β_två / 2 och a₁ = β₁ /två. Vad:

a = a₁ + a_två och β = β₁ + β_två

Därför följer att:

a = a₁ + a_två = β₁ / 2 + p_två / 2 = (β₁ + β_två) / 2 = P / 2.

Enligt egenskaperna:

a = β / 2

Eftersom vi får veta att β₁ = 60º då:

a₁ = β₁ / 2 = 60º / 2 = 30º.

De säger också att α₁ = β_två så det följer att:

β_två = 30º.

Vinkeln β resulterar:

β₁ + β_två = 60º + 30º = 90º.

Och eftersom α = β / 2, då:

α = 90º / 2 = 45º. 

Sammanfattningsvis:

β = 90º och α = 45º.

Referenser

1. Baldor, A. 1973. Geometri och trigonometri. Centralamerikanskt kulturförlag.
2. E. A. 2003. Element av geometri: med övningar och kompassgeometri. University of Medellin.
3. Geometri 1: a ESO. Vinklar på omkretsen. Återställd från: edu.xunta.es.
4. All vetenskap. Lösta problem med vinklar i omkretsen. Återställd från: francesphysics.blogspot.com
5. Wikipedia. Inskriven vinkel. Återställd från: es.wikipedia.com