
Kompletterande vinklar vad är de, beräkning, exempel, övningar
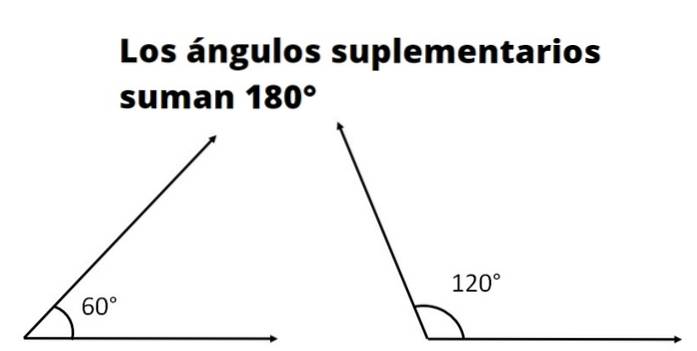
Två eller fler är det kompletterande vinklar om summan av dess mått motsvarar måttet på en rak vinkel. Måttet på en rak vinkel, även kallad en plan vinkel, i grader är 180º och i radianer är det π.
Till exempel finner vi att de tre inre vinklarna i en triangel är kompletterande, eftersom summan av deras mått är 180º. Tre vinklar visas i figur 1. Av ovanstående följer att α och β är kompletterande, eftersom de ligger intill varandra och deras summa fullbordar en rak vinkel.
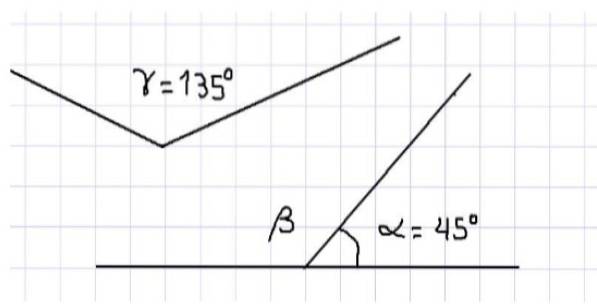
Även i samma figur har vi vinklarna α och γ som också är kompletterande, eftersom summan av deras mått är lika med måttet på en plan vinkel, det vill säga 180º. Det kan inte sägas att vinklarna β och γ är kompletterande eftersom, eftersom båda vinklarna är trubbiga, är deras mått större än 90 ° och därför överstiger deras summa 180 °.
Å andra sidan kan det konstateras att måttet på vinkeln β är lika med måttet på vinkeln γ, eftersom om β är komplement till α och γ är kompletterande med α, så är β = γ = 135º.
Artikelindex
- 1 Exempel
- 1.1 Exempel A
- 1.2 Exempel B
- 1.3 Exempel C
- 1.4 Exempel D
- 1.5 Exempel E
- 1.6 Exempel F
- 2 övningar
- 2.1 - Övning I
- 2.2 - Övning II
- 2.3 - Övning III
- 3 Kompletterande vinklar i två paralleller skurna av en sekant
- 3.1 - Övning IV
- 4 Referenser
Exempel
I följande exempel uppmanas det att hitta de okända vinklarna, indikerade med frågetecken i figur 2. De sträcker sig från de enklaste exemplen till några lite mer detaljerade att läsaren bör vara mer försiktig.
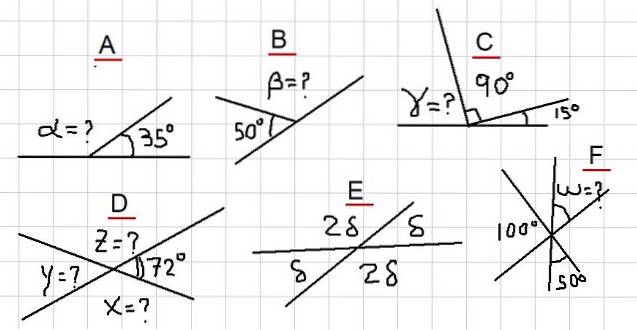
Exempel A
I figuren har vi att de intilliggande vinklarna α och 35º sammanfaller med en plan vinkel. Det vill säga α + 35º = 180º och därför är det sant att: α = 180º- 35º = 145º.
Exempel B
Eftersom β är kompletterande med vinkeln 50º, följer det att β = 180º - 50º = 130º.
Exempel C
Från figur 2C observeras följande summa: γ + 90º + 15º = 180º. Det vill säga γ är kompletterande med vinkeln 105º = 90º + 15º. Det dras därefter slutsatsen att:
γ = 180 º - 105 º = 75 º
Exempel D
Eftersom X är kompletterande med 72º följer det att X = 180º - 72º = 108º. Dessutom är Y kompletterande med X, så Y = 180º - 108º = 72º.
Och slutligen är Z kompletterande med 72º, därför är Z = 180º - 72º = 108º.
Exempel E
Vinklarna δ och 2 δ är kompletterande, därför δ + 2 δ = 180 º. Vilket innebär att 3δ = 180º, och detta tillåter oss i sin tur att skriva: δ = 180º / 3 = 60º.
Exempel F
Om vi kallar vinkeln mellan 100º och 50º U, är U kompletterande med dem, eftersom det observeras att deras summa fullbordar en plan vinkel.
Det följer omedelbart att U = 150º. Eftersom U är mittemot toppunkten mot W, är W = U = 150º.
Träning
Tre övningar föreslås nedan, i alla måste värdet av vinklarna A och B i grader hittas så att förhållandena i figur 3. Uppfylls. Begreppet kompletterande vinklar används för att lösa dem alla..
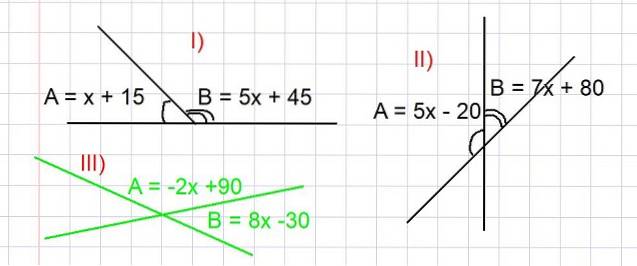
- Övning I
Bestäm värdena för vinklarna A och B från del I) i figur 3.
Lösning
A och B är kompletterande, från vilka vi har att A + B = 180 grader, då ersätts uttrycket för A och B som en funktion av x, som det visas i bilden:
(x + 15) + (5x + 45) = 180
En linjär ekvation av första ordningen erhålls. För att lösa det grupperas termerna omedelbart:
6 x + 60 = 180
Genom att dela båda medlemmarna med 6 har vi:
x + 10 = 30
Och slutligen löser det sig att x är värt 20º.
Nu måste vi ansluta värdet på x för att hitta de önskade vinklarna. Därför är vinkeln A: A = 20 +15 = 35º.
Och för sin del är vinkel B B = 5 * 20 + 45 = 145º.
- Övning II
Hitta värdena för vinklarna A och B från del II) i figur 3.
Lösning
Eftersom A och B är kompletterande vinklar har vi A + B = 180 grader. Genom att ersätta uttrycket för A och B som en funktion av x ges i del II) i figur 3 har vi:
(-2x + 90) + (8x - 30) = 180
Återigen erhålls en första grads ekvation för vilken termerna måste grupperas på ett bekvämt sätt:
6 x + 60 = 180
Genom att dela upp båda medlemmarna med 6 har vi:
x + 10 = 30
Därav följer att x är värd 20º.
Med andra ord, vinkeln A = -2 * 20 + 90 = 50º. Medan vinkel B = 8 * 20-30 = 130º.
- Övning III
Bestäm värdena för vinklarna A och B från del III) i figur 3 (i grön färg).
Lösning
Eftersom A och B är kompletterande vinklar har vi det A + B = 180 grader. Vi måste ersätta uttrycket för A och B som en funktion av x i figur 3, från vilken vi har:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Genom att dela båda medlemmarna med 12 för att lösa värdet på x har vi:
x + 5 = 15
Slutligen visar man sig att x är värt 10 grader.
Nu fortsätter vi med att ersätta vinkeln A: A = 5 * 10 -20 = 30º. Och för vinkel B: B = 7 * 10 + 80 = 150º
Kompletterande vinklar i två paralleller skurna av en sekant
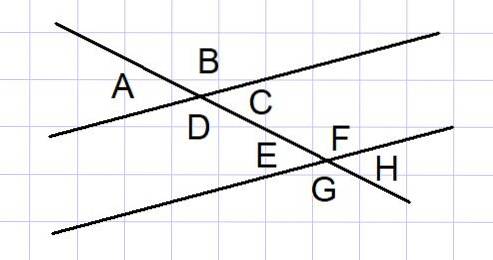
Två parallella linjer skärs av en sekant är en vanlig geometrisk konstruktion i vissa problem. Mellan sådana linjer bildas åtta vinklar som visas i figur 4.
Av dessa åtta vinklar är några vinkelpar kompletterande, vilket vi listar nedan:
- De yttre vinklarna A och B och de yttre vinklarna G och H
- De inre vinklarna D och C och de inre vinklarna E och F
- De yttre vinklarna A och G och de yttre vinklarna B och H
- Interiörvinklarna D och E och interiörerna C och F
För fullständighet heter vinklarna lika med varandra också:
- De interna alternativen: D = F och C = E
- De externa alternativen: A = H och B = G
- Motsvarande: A = E och C = H
- Motsatser efter vertex A = C och E = H
- Motsvarande: B = F och D = G
- Motsatser efter vertex B = D och F = G
- Övning IV
Med hänvisning till figur 4, som visar vinklarna mellan två parallella linjer skurna av en sekant, bestäm värdet på alla vinklar i radianer, med vetskap om att vinkeln A = π / 6 radianer.
Lösning
A och B är kompletterande yttre vinklar så B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Referenser
- Baldor, J. A. 1973. Plane and Space Geometry. Centralamerikansk kultur.
- Matematiska lagar och formler. Vinkelmätningssystem. Återställd från: ingemecanica.com.
- Wentworth, G. Plane Geometry. Återställd från: gutenberg.org.
- Wikipedia. Kompletterande vinklar. Återställd från: es.wikipedia.com
- Wikipedia. Transportband. Återställd från: es.wikipedia.com
- Zapata F. Goniómetro: historia, delar, drift. Återställd från: lifeder.com


Ingen har kommenterat den här artikeln än.