
Irrationella tal historia, egenskaper, klassificering, exempel
De irrationella siffror är de vars decimala uttryck har oändliga siffror utan ett upprepande mönster, därför kan de inte erhållas genom att göra kvoten mellan två heltal.
Bland de mest kända irrationella siffrorna är:

Bland dem är utan tvekan π (pi) det mest bekanta, men det finns många fler. Alla tillhör de reella siffrorna, som är den numeriska uppsättningen som grupperar rationella och irrationella tal..
Ellipsen i figur 1 indikerar att decimalerna fortsätter på obestämd tid. Vad som händer är att utrymmet i vanliga miniräknare bara tillåter att visa några få.
Om vi tittar noga, närhelst vi gör kvoten mellan två heltal, får vi ett decimal med begränsade siffror eller om inte, med oändliga siffror där en eller flera upprepas. Tja, detta händer inte med irrationella siffror..
Artikelindex
- 1 Historik om irrationella siffror
- 2 Egenskaper för irrationella tal
- 3 Placering av ett irrationellt nummer på den verkliga linjen
- 4 Klassificering av irrationella siffror
- 4.1 Algebraiska siffror
- 4.2 Transcendenta nummer
- 5 Träning
- 5.1 Svar
- 6 Referenser
Historien om irrationella siffror
Den stora forntida matematikern Pythagoras, född 582 f.Kr. i Samos, Grekland, grundade Pythagoras tankeskola och upptäckte den berömda satsen som bär hans namn. Vi har det här till vänster (kanske visste babylonierna det redan långt innan).
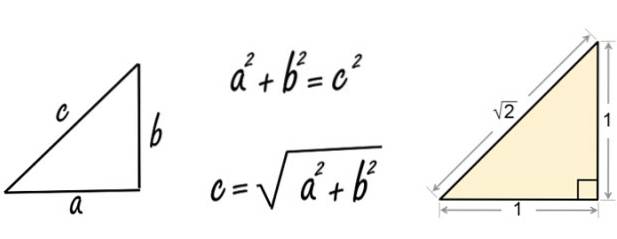
När Pythagoras (eller förmodligen en lärjunge av honom) applicerade satsen på en rätt triangel med sidor lika med 1, fann han det irrationella talet √2.
Han gjorde det så här:
c = √1två + 1två = √1 + 1 = √2
Och omedelbart insåg han att detta nya nummer inte kom från kvoten mellan två andra naturliga tal, som var de som var kända vid den tiden.
Därför kallade han det irrationell, och upptäckten orsakade stor ångest och förvirring bland pythagoreerna.
Egenskaper hos irrationella tal
-Uppsättningen av alla irrationella tal betecknas med bokstaven I och ibland som Q * eller QC. Föreningen mellan de irrationella siffrorna I eller Q * och de rationella siffrorna Q ger upphov till uppsättningen av reella tal R.
-Med irrationella tal kan de kända aritmetiska operationerna utföras: addition, subtraktion, multiplikation, division, empowerment och mer.
-Division med 0 definieras inte heller mellan irrationella tal.
-Summan och produkten mellan irrationella tal är inte nödvändigtvis ett annat irrationellt tal. Till exempel:
√2 x √8 = √16 = 4
Och 4 är inte ett irrationellt tal.
-Summan av ett rationellt tal plus ett irrationellt tal resulterar dock i ett irrationellt tal. På det här sättet:
1 + √2 = 2.41421356237 ...
-Produkten av ett annat rationellt tal än 0 med ett irrationellt tal är också irrationellt. Låt oss titta på det här exemplet:
2 x √2 = 2.828427125 ...
-Det omvända av en irrationell resulterar i ett annat irrationellt tal. Låt oss prova några:
1 / √2 = 0,707106781 ...
1 / √3 = 0.577350269 ...
Dessa siffror är intressanta eftersom de också är värdena för vissa trigonometriska förhållanden av kända vinklar. De flesta trigonometriska förhållandena är irrationella tal, men det finns undantag, såsom sin 30º = 0,5 = ½, vilket är rationellt.
-Dessutom uppfylls kommutativa och associerande egenskaper. Om a och b är två irrationella tal betyder detta att:
a + b = b + a.
Och om c är ett annat irrationellt tal, då:
(a + b) + c = a + (b + c).
-Den fördelande egenskapen för multiplikation med avseende på addition är en annan välkänd egenskap som också gäller för irrationella tal. I detta fall:
a. (b + c) = a.b + a.c.
-En irrationell a har sin motsats: -a. När de läggs samman är resultatet 0:
a + (- a) = 0
-Mellan två olika rationella finns det minst ett irrationellt tal.
Plats för ett irrationellt nummer på den verkliga linjen
Den verkliga linjen är en horisontell linje där de verkliga siffrorna finns, av vilka irrationella är en viktig del.
För att hitta ett irrationellt tal på den verkliga linjen, i geometrisk form, kan vi använda Pythagoras sats, en linjal och en kompass.
Som ett exempel ska vi lokalisera √5 på den riktiga linjen, för vilken vi ritar en rätt triangel med sidor x = 2 Y y = 1, som bilden visar:
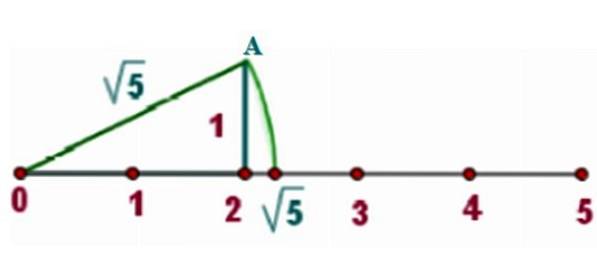
Enligt Pythagoras sats är hypotenusen i en sådan triangel:
c = √2två + 1två = √4 + 1 = √5
Nu placeras kompassen med punkten 0, där en av höjderna i höger triangel också är. Kompasspennans punkt ska ligga vid toppunkt A.
En cirkelbåge dras som skär till den verkliga linjen. Eftersom avståndet mellan omkretsens centrum och vilken punkt som helst på den är radien, vilken är lika med √5, är skärningspunkten också långt √5 från centrum.
Från diagrammet kan man se att √5 är mellan 2 och 2,5. En miniräknare ger oss det ungefärliga värdet av:
√5 = 2,236068
Och så, genom att bygga en triangel med lämpliga sidor, kan andra irrationella sådana lokaliseras, såsom √7 och andra.
Klassificering av irrationella siffror
Irrationella siffror klassificeras i två grupper:
-Algebraisk
-Transcendent eller transcendent
Algebraiska siffror
Algebraiska tal, som kan eller inte kan vara irrationella, är lösningar på polynomekvationer vars allmänna form är:
tilln xn + tilln-1xn-1 + tilln-2xn-2 +.... + a1x + aeller = 0
Ett exempel på en polynomekvation är en kvadratisk ekvation som denna:
x3 - 2x = 0
Det är lätt att visa att det irrationella talet √2 är en av lösningarna i denna ekvation.
Transcendenta siffror
Å andra sidan uppstår de transcendenta siffrorna, även om de är irrationella, aldrig som en lösning av en polynomekvation.
De transcendenta siffrorna som finns oftast i tillämpad matematik är π på grund av dess förhållande till omkretsen och antalet e, eller Eulers nummer, som är basen för naturliga logaritmer..
Övning
En grå fyrkant placeras på en svart fyrkant i den position som anges i figuren. Ytan på den svarta fyrkanten är känd för att vara 64 cmtvå. Hur mycket är längden på båda rutorna?

Svar
Området för en kvadrat med sidan L är:
A = L.två
Eftersom den svarta fyrkanten är 64 cmtvå av ytan, bör dess sida vara 8 cm.
Denna mätning är densamma som diagonalen av den grå fyrkanten. Genom att tillämpa Pythagoras sats på denna diagonal och komma ihåg att sidorna av en kvadrat mäter samma, kommer vi att ha:
8två = Lgtvå + Lgtvå
Där Lg är sidan av den grå fyrkanten.
Därför: 2Lgtvå = 8två
Tillämpa kvadratrot på båda sidor av jämställdheten:
Lg = (8 / √2) cm
Referenser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 2000. Matematik 9: e. Kvalitet. CO-BO-utgåvor.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Utbildningsportal. Irrationella siffror och deras egenskaper. Återställd från: portaleducativo.net.
- Wikipedia. Irrationella siffror. Återställd från: es.wikipedia.org.


Ingen har kommenterat den här artikeln än.