
Transcendenta tal vad är de, formler, exempel, övningar
De transcendenta siffror är de som inte kan erhållas som ett resultat av en polynomekvation. Motsatsen till ett transcendent tal är a algebraiskt nummer, vilka är lösningar av en polynomekvation av typen:
tilln xn + tilln-1 xn-1 +... + Atvå xtvå + till1 x + a0 = 0
Där koefficienterna an, tilln-1,... tilltvå, till1, till0 är rationella nummer, kallade polynomens koefficienter. Om ett tal x är en lösning på den föregående ekvationen är det numret inte transcendent.

Vi analyserar några siffror och ser om de är transcendenta eller inte:
a) 3 är inte transcendent eftersom det är en lösning av x - 3 = 0.
b) -2 kan inte vara transcendent eftersom det är en lösning av x + 2 = 0.
c) ⅓ är en lösning av 3x - 1 = 0
d) En lösning av ekvationen xtvå - 2x + 1 = 0 är √2 -1, så att talet per definition inte är transcendent.
e) Inte heller √2 eftersom det är resultatet av ekvationen xtvå - 2 = 0. Kvadrering √2 ger resultatet 2, som subtraheras från 2 är lika med noll. Så √2 är ett irrationellt tal men det är inte transcendent.
Artikelindex
- 1 Vad är transcendenta tal?
- 1.1 Siffran π
- 1.2 Siffran e
- 2 Formler där det transcendenta numret π visas
- 2.1 Omkretsens omkrets
- 2.2 Område av en cirkel
- 2.3 En sfärs yta
- 2.4 Sfärens volym
- 3 Övningar
- 3.1 - Övning 1
- 3.2 - Övning 2
- 4 Referenser
Vad är transcendenta tal?
Problemet är att det inte finns någon allmän regel för att få dem (senare kommer vi att säga ett sätt), men några av de mest kända är antalet pi och den Nollnummer, betecknas med: π Y och.
Siffran π
Numret π Det verkar naturligt genom att observera att den matematiska kvoten mellan omkretsen P för en cirkel och dess diameter D, oavsett om det är en liten eller stor cirkel, alltid ger samma antal, kallat pi:
π = P / D ≈ 3.14159 ...
Detta innebär att om omkretsens diameter tas som måttenhet, för dem alla, stora eller små, kommer omkretsen alltid att vara P = 3,14 ... = π, som kan ses i animationen i figur 2.
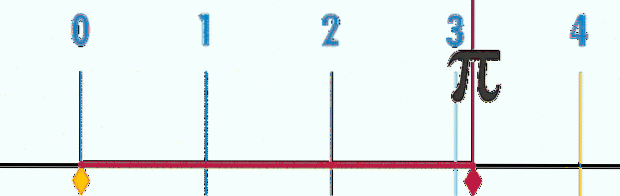
För att bestämma fler decimaler är det nödvändigt att mäta P och D med större precision och sedan beräkna kvoten, vilket har gjorts matematiskt. Slutsatsen är att kvotens decimaler inte har något slut och aldrig upprepar sig, så siffran π förutom att vara transcendent är det också irrationell.
Ett irrationellt tal är ett tal som inte kan uttryckas som delningen av två heltal.
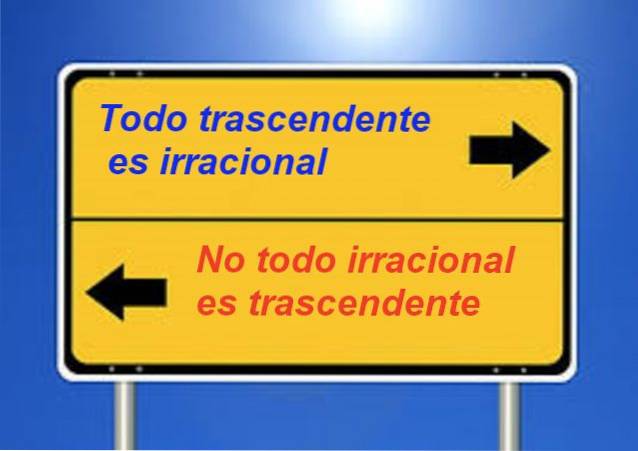
Det är känt att varje transcendent nummer är irrationellt, men det är inte sant att alla irrationella tal är transcendenta. Exempelvis är √2 irrationell, men det är inte transcendent.
Siffran e
Det transcendenta talet e är basen för naturliga logaritmer och dess decimala approximation är:
e ≈ 2.718281828459045235360 ... .
Om du ville skriva numret och exakt skulle det vara nödvändigt att skriva oändliga decimaler, för varje transcendent tal är irrationellt, som sagt tidigare.
De första tio siffrorna i och är lätta att komma ihåg:
2,7 1828 1828 och även om det verkar följa ett repetitivt mönster, uppnås detta inte i decimaler av ordning större än nio.
En mer formell definition av och är nästa:
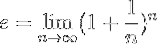
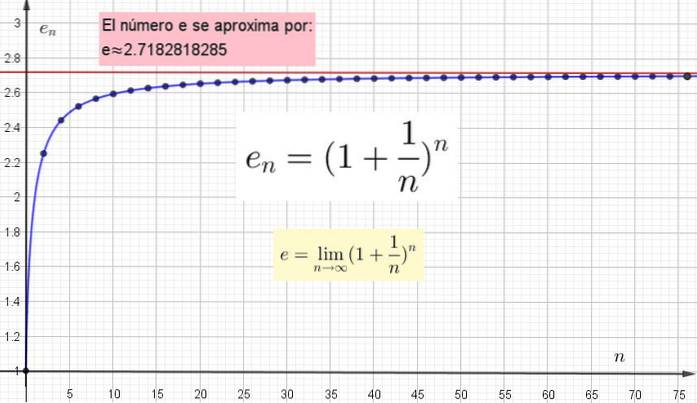
Vilket innebär att det exakta värdet av och uppnås genom att utföra den operation som anges i denna formel, när det naturliga talet n tenderar till oändlighet.
Detta förklarar varför vi bara kan få approximationer av och, eftersom oavsett hur stort antalet n är placerat kommer det alltid att vara möjligt att hitta en n högre.
Låt oss leta efter några approximationer på egen hand:
-När n = 100 då (1 + 1/100)100 = 2,70481 som knappast sammanfaller med första decimal med det "sanna" värdet på e.
-Om du väljer n = 10.000 har du (1 + 1 / 10.000)10.000 = 2.71815 som matchar det "exakta" värdet av e på de tre första decimalerna.
Denna process måste följas oändligt för att få det "sanna" värdet av e. Jag tror inte att vi har tid att göra det, men låt oss prova en till:
Låt oss använda n = 100.000:
(1 + 1 / 100.000)100.000 = 2.7182682372
Det har bara fyra decimaler som matchar det värde som anses exakt.
Det viktiga är att förstå att ju högre värdet på n valt att beräkna en, ju närmare det är det verkliga värdet. Men det verkliga värdet kommer bara att uppnås när n är oändlig.
Andra viktiga siffror
Förutom dessa kända nummer finns det andra transcendenta nummer, till exempel:
- två√2
Varje algebraiskt tal, annat än 0 eller 1, som höjs till en irrationell exponent kommer att vara ett transcendent tal.
-Champernowne-numret i bas 10:
C_10 = 0.123456789101112131415161718192021 ... .
-Champernowne-numret i bas 2:
C_2 = 0.1101110010110111 ... .
-Gamma-talet γ eller Euler-Mascheroni-konstanten:
γ ≈ 0,577 215 664 901 532 860 606
Vilket erhålls genom att göra följande beräkning:
γ ≈ 1 + ½ + ⅓ + ¼ + ... + 1 / n - ln (n)
När n vara väldigt väldigt stor. För att ha det exakta värdet på gammanumret måste du göra beräkningen med n oändlig. Något liknande det vi gjorde ovan.
Och det finns många fler transcendenta siffror. Den stora matematikern Georg Cantor, född i Ryssland och som bodde mellan 1845 och 1918, visade att uppsättningen transcendenta tal är mycket större än uppsättningen algebraiska tal.
Formler där det transcendenta numret π visas
Omkretsens omkrets
P = π D = 2 π R, där P är omkretsen, D diametern och R omkretsens radie. Man bör komma ihåg att:
-Omkretsens diameter är det längsta segmentet som förenar två punkter av samma och som alltid passerar genom dess centrum,
-Radien är halva diametern och är det segment som går från centrum till kanten.
Område av en cirkel
A = π Rtvå = ¼ π Dtvå
Ytan på en sfär
S = 4 π Rtvå.
Ja, även om det kanske inte verkar så är ytan på en sfär densamma som den för fyra cirklar med samma radie som sfären..
Sfärens volym
V = 4/3 π R3
Träning
- Övning 1
Pizzerian “EXÓTICA” säljer pizzor med tre diametrar: små 30 cm, medelstora 37 cm och stora 45 cm. Ett barn är mycket hungrigt och han insåg att två små pizzor kostar samma som en stor. Vad som är bättre för honom, köp två små pizzor eller en stor?

Lösning
Ju större område, desto större mängd pizza, av denna anledning beräknas arean för en stor pizza och jämförs med den för två små pizzor:
Stort pizzaområde = ¼ π Dtvå = ¼ ⋅3.1416⋅45två = 1590,44 cmtvå
Litet pizzaområde = ¼ π dtvå = ¼ ⋅3.1416⋅30två = 706,86 cmtvå
Därför har två små pizzor ett område på
2 x 706,86 = 1413,72 cmtvå .
Det är tydligt: du kommer att få mer pizza att köpa en enda stor än två små.
- Övning 2
Pizzerian “EXÓTICA” säljer också en halvklotisk pizza med en radie på 30 cm till samma pris som en rektangulär form med en sida på 30 x 40 cm. Vilket skulle du välja?

Lösning
Som nämnts i föregående avsnitt är ytan på en sfär fyra gånger den för en cirkel med samma diameter, så en halvklot 30 cm i diameter kommer att ha:
12 '' halvklotisk pizza: 1413,72 cmtvå (två gånger en cirkel med samma diameter)
Rektangulär pizza: (30 cm) x (40 cm) = 1200 cmtvå .
Den halvklotiska pizzaen har ett större område.
Referenser
- Fernández J. Siffran e. Ursprung och nyfikenheter. Återställd från: soymatematicas.com
- Njut av matematik. Eulers nummer. Återställd från: gustolasmatematicas.com.
- Figuera, J. 2000. Matematik 1: a. Diversifierad. CO-BO-utgåvor.
- García, M. Siffran e i elementär kalkyl. Återställd från: matematica.ciens.ucv.ve.
- Wikipedia. PI-nummer. Återställd från: wikipedia.com
- Wikipedia. Transcendenta siffror. Återställd från: wikipedia.com



Ingen har kommenterat den här artikeln än.