
Orthoederformler, area, volym, diagonal, exempel
De ortoeder Det är en volymetrisk eller tredimensionell geometrisk figur som kännetecknas av att ha sex rektangulära ytor, så att de motsatta ytorna är i parallella plan och är identiska eller kongruenta rektanglar. Å andra sidan är ansikten intill ett givet ansikte i plan vinkelrätt mot det ursprungliga ansiktet..
Det kan också övervägas ortoeder som ett ortogonalt prisma med en rektangulär bas, i vilken dihedral vinklar bildas av planen med två ytor intill en gemensam kant, de mäter 90º. Den tvåkantiga vinkeln mellan två ytor mäts på skärningspunkten mellan ansikten med ett vinkelrätt plan gemensamt för dem.
På samma sätt är ortohedronen en rektangel parallellpipad, eftersom detta är hur parallellpiped definieras som den volymetriska figuren av sex ytor, som är parallella två och två.
I alla parallellpipade är ytorna parallellogram, men i de rektangulära parallellpipade ytorna måste de vara rektangulära.
Artikelindex
- 1 Delar av ortohedronen
- 2 Orthoederformler
- 2.1 Område
- 2.2 Volym
- 2.3 Intern diagonal
- 3 Exempel
- 3.1 - Exempel 1
- 3.2 - Övning 2
- 4 Referenser
Delar av ortohedronen
Delarna av en polyeder, såsom ortoeder, Dom är:
-Kanter
-Hörn
-Ansikten
Vinkeln mellan två kanter på en yta av ortoedern sammanfaller med den tvåvinklade vinkeln som bildas av dess andra två ytor intill var och en av kanterna och bildar en rät vinkel. Följande bild klargör varje koncept:
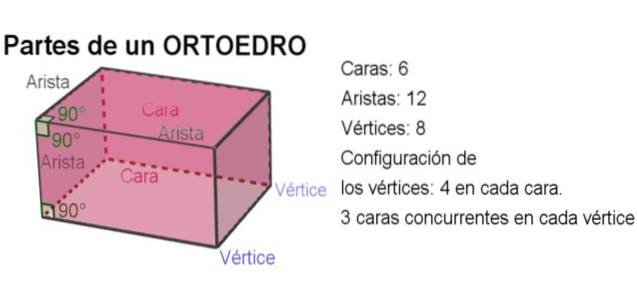
-Totalt har en ortohedron 6 ansikten, 12 kanter och 8 hörn..
-Vinkeln mellan två kanter är en rät vinkel.
-Den tvåkantiga vinkeln mellan två ansikten är också rätt.
-I varje ansikte finns fyra toppar och i varje toppunkt stämmer tre ömsesidigt ortogonala ansikten samman.
Orthoederformler
Område
Ytan eller ytan på en ortoeder är summan av områdena i deras ansikten.
Om de tre kanterna som möts vid en topp har mått a, b och c, som visas i figur 3, har framsidan area c⋅b och bottenytan har också area c⋅b.
Sedan har de två sidoytorna yta a⋅b varje. Och slutligen har golv- och takytorna yta före Kristus varje.
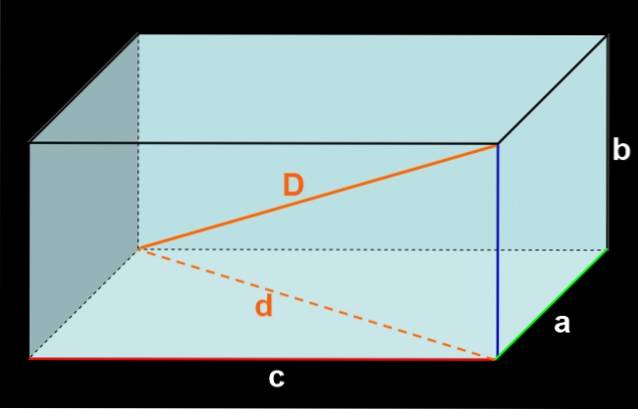
Att lägga till området för alla ansikten ger:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Att ta en gemensam faktor och beställa villkoren:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Volym
Om ortoedern betraktas som ett prisma beräknas dess volym enligt följande:
Volym = Areal av prisma bas x prisma höjd
I detta fall tas måttgolvet som den rektangulära basen c Y till, då är basområdet c⋅a.
Höjden ges av längden b från ortogonala kanter till sidoytor till Y c.
Multiplicera basområdet (före Kristus) efter höjd b du har volymen V av ortohedronen:
V = a⋅b⋅c
Intern diagonal
I en ortoeder finns två typer av diagonaler: de yttre diagonalerna och de inre diagonalerna.
De yttre diagonalerna är på de rektangulära ytorna, medan de inre diagonalerna är segmenten som sammanfogar två motsatta hörn, förstås av motsatta hörn de som inte delar någon kant.
I en ortoeder finns fyra inre diagonaler, alla lika stora. Längden på de inre diagonalerna kan erhållas genom att tillämpa Pythagoras sats för rätt trianglar.
Längden d av den yttre diagonalen på ortohedrons golvyta uppfyller det pythagoriska förhållandet:
dtvå = atvå + ctvå
På samma sätt uppfyller den inre diagonalen av mått D det pythagoreiska förhållandet:
Dtvå = dtvå + btvå.
Kombinera de två tidigare uttrycken vi har:
Dtvå = atvå + ctvå + btvå.
Slutligen ges längden på någon av de inre diagonalerna i ortoederna med följande formel:
D = √ (atvå + btvå + ctvå ).
Exempel
- Exempel 1
En murare bygger en tank i form av en ortoeder vars inre mått är: 6 m x 4 m i bas och 2 m i höjd. Det frågar:
a) Bestäm tankens inre yta om den är helt öppen uppe.
b) Beräkna volymen på tankens inre utrymme.
c) Hitta längden på en inre diagonal.
d) Hur stor är tankens kapacitet i liter?
Lösning till
Vi tar måtten på den rektangulära basen a = 4 m och c = 6 m och höjden som b = 2 m
Området för en ortohedron med de angivna dimensionerna ges av följande förhållande:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
Nämligen:
A = 2⋅ (8 mtvå + 12 mtvå + 24 mtvå) = 2⋅ (44 mtvå) = 88 mtvå
Det tidigare resultatet är området för den stängda ortohedronen med de angivna dimensionerna, men eftersom det är en tank helt täckt i sin övre del, för att få ytan på tankens inre väggar, området för det saknade locket måste subtraheras, vilket är:
c⋅a = 6 m ⋅ 4 m = 24 mtvå.
Slutligen kommer tankens inre yta att vara: S = 88 mtvå - 24 mtvå = 64 mtvå.
Lösning b
Tankens inre volym ges av volymen på en ortoeder med tankens inre dimensioner:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Lösning c
Den inre diagonalen för en oktaeder med dimensionerna på tankens inre har en längd D som ges av:
√ (tilltvå + btvå + ctvå ) = √ ((4 m)två + (2 m)två + (6 m)två )
Genomföra de angivna operationerna vi har:
D = √ (16 mtvå + 4 mtvå + 36 mtvå ) = √ (56 mtvå) = 2√ (14) m = 7,48 m.
Lösning d
För att beräkna tankens kapacitet i liter är det nödvändigt att veta att volymen på en kubikdecimeter är lika med kapaciteten på en liter. Det hade tidigare beräknats i volym i kubikmeter, men det måste omvandlas till kubikdecimeter och sedan till liter:
V = 48 m3 = 48 (10 dm)3 = 4800 dm3 = 4800 L.
- Övning 2
Ett glasakvarium har en kubisk form med en sida på 25 cm. Bestäm området i mtvå, volymen i liter och längden på en inre diagonal i cm.
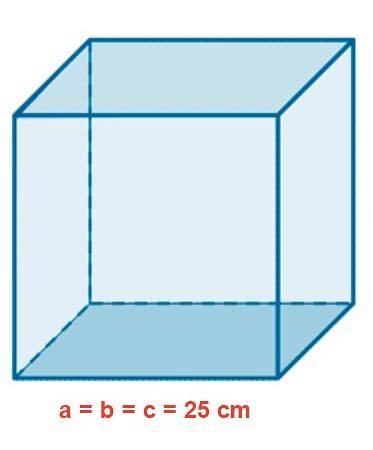
Lösning
Området beräknas med samma orthoederformel, men med hänsyn till att alla dimensioner är identiska:
A = 2⋅ (3 a⋅a) = 6⋅ atvå = 6⋅ (25 cm)två = 1 250 cmtvå
Kubens volym ges av:
V = a3 = (25 cm)3 = 15,625 cm3 = 15,625 (0,1 dm)3 = 15 625 dm3 = 15,625 L..
Längden D på den inre diagonalen är:
D = √ (3atvå) = 25√ (3) cm = 43,30 cm.
Referenser
- Arias J. GeoGebra: Prisma. Återställd från: youtube.com.
- Calculus.cc. Övningar och lösta problem i områden och volymer. Återställd från: calculo.cc.
- Salvador R. Pyramid + ortohedron med GEOGEBRA (IHM). Återställd från: youtube.com
- Weisstein, Eric. "Orthohedron". MathWorld. Wolfram Research.
- Wikipedia. Orthoeder Återställd från: es.wikipedia.com


Ingen har kommenterat den här artikeln än.