
Linjär programmering vad den är avsedd för, modeller, begränsningar, applikationer
De linjär programmering är en matematisk metod som används för att optimera (maximera eller minimera efter behov) en funktion vars variabler är föremål för begränsningar, så länge som funktionen och begränsningarna är linjärt beroende av variablerna.
Generellt är den funktion som ska optimeras modellera en praktisk situation, såsom vinsten hos en tillverkare vars insatsvaror, arbete eller maskiner är begränsade.

Ett av de enklaste fallen är att en linjär funktion ska maximeras, vilket bara beror på två variabler, kallade beslutsvariabler. Det kan ha formen:
Z = k1x + ktvåY
Med k1 och ktvå konstant. Denna funktion kallas Objektiv funktion. Naturligtvis finns det situationer som förtjänar mer än två variabler för studier, eftersom de är mer komplexa:
Z = k1x1 + ktvåxtvå + k3x3 +... .
Och begränsningarna modelleras också matematiskt av ett system av ekvationer eller ojämlikheter, lika linjära x och Y.
Uppsättningen av lösningar för detta system kallas genomförbara lösningar eller möjliga poäng. Och bland de möjliga punkterna finns det åtminstone en som optimerar objektivfunktionen.
Linjär programmering utvecklades oberoende av den amerikanska fysikern och matematikern George Dantzig (1914-2005) och den ryska matematikern och ekonomen Leonid Kantorovich (1912-1986) strax efter andra världskriget..
Felsökningsmetoden känd som simplex-metoden Det är hjärnbarnet till Dantzig, som arbetade för US Air Force, University of Berkeley och Stanford University.

Artikelindex
- 1 Linjära programmeringsmodeller
- 2 Exempel på modell
- 3 Lösningsmetoder
- 3.1 - Grafisk eller geometrisk metod
- 3.2 - Dantzigs simplexmetod
- 4 applikationer
- 5 Övningar lösta
- 5.1 - Övning 1
- 5.2 - Övning 2
- 6 Referenser
Linjära programmeringsmodeller
De element som krävs för att upprätta en linjär programmeringsmodell, lämplig för en praktisk situation, är:
-Objektiv funktion
-Beslutsvariabler
-Begränsningar
I objektivfunktionen definierar du vad du vill uppnå. Antag till exempel att du vill maximera dina vinster från tillverkning av vissa produkter. Då etableras "vinst" -funktionen enligt det pris till vilket produkterna säljs.
I matematiska termer kan denna funktion uttryckas förkortad med summeringsnotationen:
Z = ∑ki xi
I denna ekvation, ki är koefficienter och xi är beslutsvariablerna.
Beslutsvariablerna är elementen i systemet vars kontroll har och deras värden är positiva reella tal. I det föreslagna exemplet är beslutsvariablerna kvantiteten av varje produkt som ska tillverkas för att uppnå maximal vinst.
Slutligen har vi begränsningarna, vilka är linjära ekvationer eller ojämlikheter när det gäller beslutsvariablerna. De beskriver begränsningarna till problemet, som är kända och kan till exempel vara de kvantiteter råmaterial som finns tillgängliga vid tillverkningen..
Typer av begränsningar
Du kan ha M antal begränsningar, från och med j = 1 fram tills j = M. Matematiskt är begränsningarna av tre typer:
- TILLj = ∑ aI j . xi
- Bj ≥ ∑ bI j . xi
- Cj ≤ ∑ cI j . xi
Den första begränsningen är av linjär ekvationstyp och betyder att värdet Aj, som är känt, måste respekteras.
De återstående två begränsningarna är linjära ojämlikheter och det betyder att B-värdenaj och Cj, kända kan de respekteras eller överskridas när den visade symbolen är ≥ (större än eller lika med) eller respekteras eller inte överskrids, om symbolen är ≤ (mindre än eller lika med).
Modellexempel
Användningsområdena är mycket olika, allt från företagsadministration till näring, men för att förstå metoden föreslås en enkel modell av en praktisk situation med två variabler..
En lokal konditori är känd för två specialiteter: svart skogskakan och sacripantina-kakan..
Vid beredningen kräver de ägg och socker. För svarta skogen behöver du 9 ägg och 500 g socker, medan du för sacripantine behöver 8 ägg och 800 g socker. Respektive försäljningspriser är $ 8 och $ 10.
Problemet är: Hur många kakor av varje typ måste bakverket göra för att maximera vinsten, med vetskap om att det har 10 kilo socker och 144 ägg?
Beslutsvariabler
Beslutsvariablerna är "x" och "y", som tar verkliga värden:
-x: antalet svarta skogskakor
-och: sacripantina-kakorna.
Begränsningar
Begränsningarna ges av det faktum att antalet kakor är en positiv kvantitet och det finns begränsade mängder råvara för att bereda dem..
Därför, i matematisk form, har dessa begränsningar formen:
- x ≥ 0
- och ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Begränsningar 1 och 2 utgör icke-negativitetstillstånd tidigare och alla ojämlikheter som uppkommit är linjära. I begränsningar 3 och 4 är de värden som inte får överskridas: 144 ägg och 10 kg socker.
Objektiv funktion
Slutligen är målfunktionen den vinst som erhålls vid tillverkning av "x" -mängden svarta skogskakor plus "y" -mängd sacripantiner. Den byggs genom att multiplicera priset med kvantiteten kakor som gjorts och lägga till för varje typ. Det är en linjär funktion som vi kommer att kalla G (x, y):
G = 8x + 10y
Lösningsmetoder
De olika lösningsmetoderna inkluderar grafiska metoder, simplexalgoritmen och den inre punktmetoden, för att nämna några..
- Grafisk eller geometrisk metod
När du har ett problem med två variabler som det i föregående avsnitt bestämmer begränsningarna ett månghörnigt område i planet xy, ring upp genomförbar region eller lönsamhetsregion.
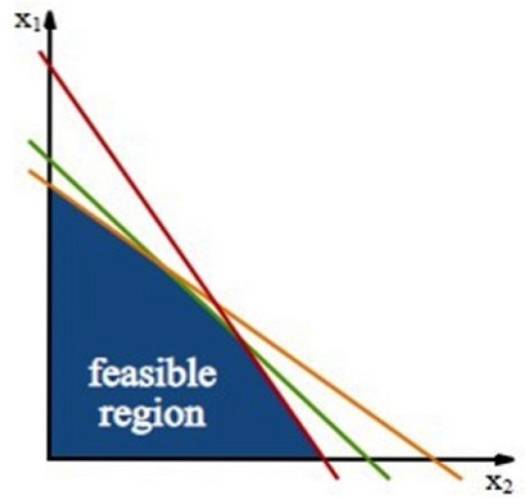
Denna region byggs med hjälp av begränsningslinjer, vilka är de linjer som erhålls från ojämlikheten i begränsningarna, som bara arbetar med jämställdhetstecknet.
När det gäller bageriet som vill optimera vinsten är begränsningslinjerna:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8 y = 10
Alla punkter i regionen som omges av dessa rader är möjliga lösningar, så det finns oändligt många av dem. Förutom i det fall det möjliga området visar sig vara tomt, i vilket fall det uppställda problemet inte har någon lösning.
Lyckligtvis är det genomförbara området för bakverkproblemet inte tomt, vi har det nedan.
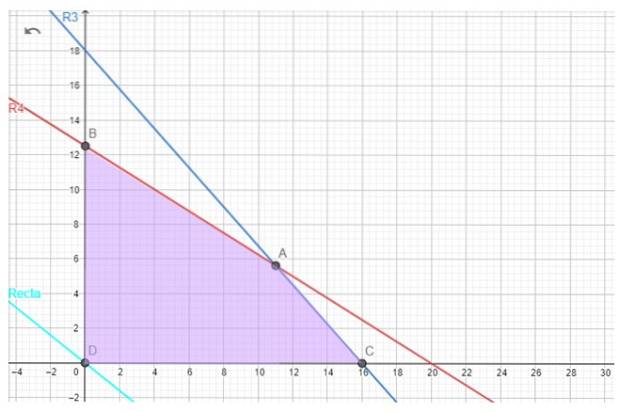
Den optimala lösningen, om den existerar, finns med hjälp av objektivfunktionen. Till exempel, när vi försöker hitta den maximala förstärkningen G, har vi följande rad, som kallas iso-vinstlinje:
G = k1x + ktvåy → y = -k1x / ktvå + G / ktvå
Med denna linje får vi alla paren (x, y) som ger en given förstärkning G, så det finns en familj av linjer enligt värdet på G, men alla med samma lutning -k1 / ktvå, så de är parallella linjer.
Den optimala lösningen
Nu kan det visas att den optimala lösningen av ett linjärt problem alltid är en extrem punkt eller toppunkt för det möjliga området. Sedan:
Lösningslinjen är den längst ifrån ursprunget och har minst en punkt gemensamt med den möjliga regionen.
Om linjen närmast ursprunget har ett helt segment gemensamt med det möjliga området sägs det att det finns oändliga lösningar. Detta fall inträffar om lutningen för iso-vinstlinjen är lika med den för någon av de andra linjerna som begränsar regionen.
För vårt bakverk är kandidathörnpunkterna A, B och C.
- Dantzigs simplexmetod
Den grafiska eller geometriska metoden är tillämplig för två variabler. Det är dock mer komplicerat när det finns tre variabler och omöjligt att använda för ett större antal variabler..
När man hanterar problem med mer än två variabler, simplex-metoden, som består av en serie algoritmer för att optimera målfunktionerna. Matriser och enkel aritmetik används ofta för att utföra beräkningarna.
Simplex-metoden börjar med att välja en genomförbar lösning och kontrollera om den är optimal. Om så är fallet har vi redan löst problemet, men om det inte är det, fortsätter vi mot en lösning närmare optimering. Om lösningen finns hittar algoritmen den i några försök.
Applikationer
Linjär och icke-linjär programmering används i många fält för att fatta de bästa besluten när det gäller att sänka kostnaderna och öka vinsten, vilket inte alltid är monetärt, eftersom de kan mätas i tid, till exempel om du vill minimera den nödvändiga tiden att utföra en serie operationer.
Här är några fält:
-Vid marknadsföring används den för att hitta den bästa kombinationen av media (sociala nätverk, tv, press och andra) för att marknadsföra en viss produkt.
-För tilldelning av adekvata uppgifter till personalen i ett företag eller fabrik eller scheman till dem.
-Vid valet av den mest näringsrika maten och till lägsta kostnad inom boskap och fjäderfäindustri.
Lösta övningar
- Övning 1
Lös grafiskt den linjära programmeringsmodellen som tagits upp i föregående avsnitt.
Lösning
Det är nödvändigt att rita upp den uppsättning värden som bestäms av det begränsningssystem som anges i problemet:
- x ≥ 0
- och ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Regionen som ges av ojämlikhet 1 och 2 motsvarar den första kvadranten i det kartesiska planet. När det gäller ojämlikhet 3 och 4 börjar vi med att hitta begränsningslinjerna:
9x + 8y = 144
0,5 x + 0,8 y = 10 → 5 x + 8 y = 100
Den genomförbara regionen är en fyrsidig vars hörn är punkterna A, B, C och D..
Minsta vinst är 0, därför är raden 8x + 10y = 0 den nedre gränsen och iso-vinstlinjerna har lutning -8/10 = - 0,8.
Detta värde skiljer sig från sluttningarna på de andra begränsningslinjerna och eftersom det möjliga området är begränsat finns den unika lösningen.
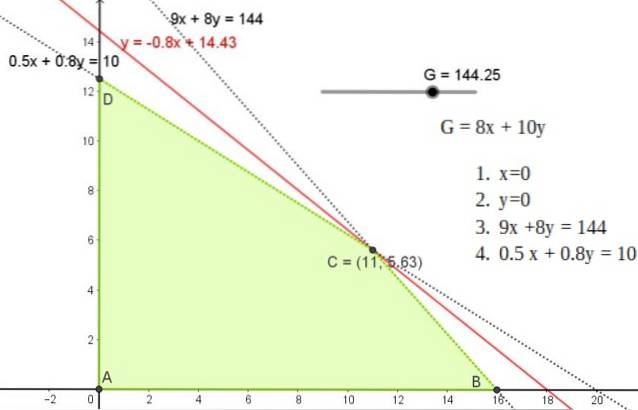
Denna lösning motsvarar en linje med lutning -0,8 som passerar genom någon av punkterna A, B eller C, vars koordinater är:
A (11; 5,625)
B (0; 12,5)
C (16, 0)
Optimal lösning
Vi beräknar värdet på G för var och en av dessa punkter:
-(11; 5,625): GTILL = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): GB = 8 x 0 + 10 x 12,5 = 125
-(16, 0): GC = 8 x 16 + 10 x 0 = 128
Den högsta vinsten finns i tillverkningen av 11 svarta skogskakor och 5625 sakripantinkakor. Denna lösning matchar den som hittas genom programvaran.
- Övning 2
Verifiera resultatet av föregående övning med hjälp av lösningsfunktionen som finns i de flesta kalkylblad som Excel eller LibreOffice Calc, som innehåller Simplex-algoritmen för optimering i linjär programmering.
Lösning
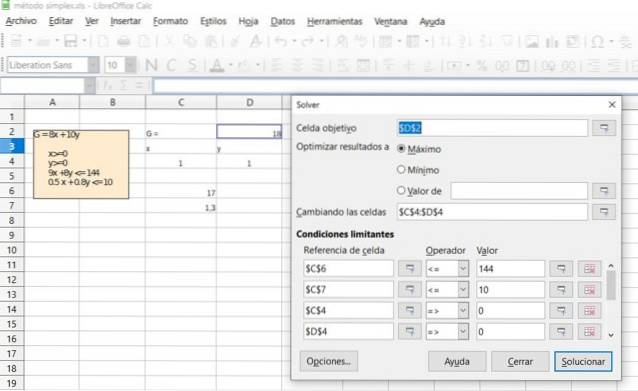
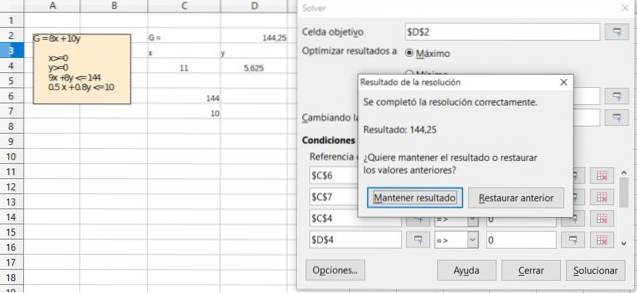
Referenser
- Lysande. Linjär programmering. Återställd från: brilliant.org.
- Eppen, G. 2000. Operationsforskning inom administrativ vetenskap. 5: e. Utgåva. Prentice hall.
- Haeussler, E. 1992. Matematik för management och ekonomi. 2: a. Utgåva. Grupo Ledare Iberoamericana.
- Hiru.eus. Linjär programmering. Återställd från: hiru.eus.
- Wikipedia. Linjär programmering. Återställd från: es. wikipedia.org.

Ingen har kommenterat den här artikeln än.