Geometrisk optik vad den studerar, lagar, tillämpningar, övningar

De geometrisk optik är den gren av fysik som fokuserar på att studera hur ljuset sprids och reflekteras när det passerar från ett medium till ett annat, utan att ta hänsyn till effekterna av diffraktion.

På detta sätt representeras ljus geometriskt av strålar, imaginära linjer vinkelrätt mot ljusvågsfronten..

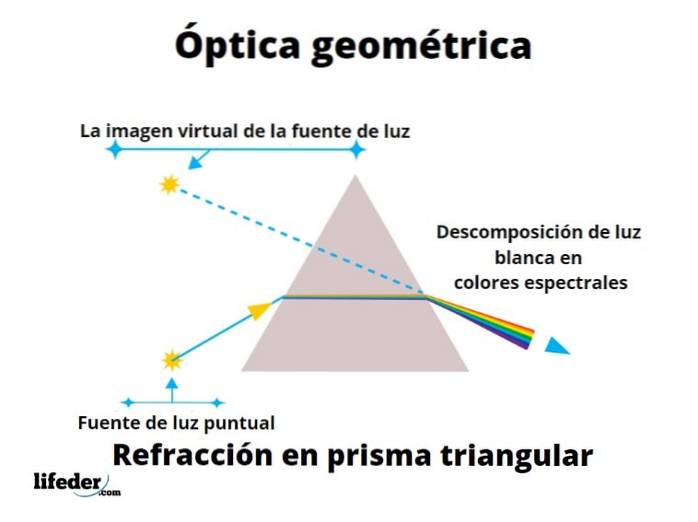
Ljusstrålar dyker upp från ljuskällor som solen, en låga eller en glödlampa som sprider sig i alla riktningar. Ytor reflekterar delvis dessa ljusstrålar och det är därför vi kan se dem tack vare att ögonen innehåller ljuskänsliga element.

Tack vare strålbehandlingen tar geometrisk optik inte så mycket hänsyn till ljusets vågaspekter, utan förklarar snarare hur bilder bildas i ögat, speglar och projektorer, var de gör det och hur de visas.

De grundläggande principerna för geometrisk optik är reflektion och brytning av ljus. Ljusstrålar slår i vissa vinklar på ytorna de möter, och tack vare detta hjälper en enkel geometri att hålla reda på deras bana i varje medium.

Detta förklarar vardagliga saker som att titta på vår bild i badrumsspegeln, se en tesked som verkar böja sig inuti ett glas fullt av vatten eller förbättra synen med rätt glasögon..

Vi behöver ljus för att relatera till miljön, det är därför dess beteende alltid har förvånat observatörer som undrade om dess natur..

Artikelindex

• 1 Vad studerar geometrisk optik? (Studieobjekt)
• 2 Grundläggande begrepp inom geometrisk optik
  • 2.1 Brytningsindex
  • 2.2 Optisk väg
• 3 Lagar om geometrisk optik
  • 3.1 Fermats princip
  • 3.2 Reflektionslag
  • 3.3 Snells lag
• 4 applikationer
  • 4.1 Speglar och linser
  • 4.2 Optiska instrument
  • 4.3 Optisk fiber
• 5 Övningen löst
  • 5.1 Lösning
• 6 Referenser

Vad studerar geometrisk optik? (Studieobjekt)

Geometrisk optik studerar spridning av ljus i ett vakuum och i olika medier utan att förklara vad dess sanna natur består av. För detta använder den strålmodellen och enkel geometri.

En stråle är vägen som ljuset följer i ett visst transparent medium, vilket är en utmärkt approximation så länge våglängden är liten jämfört med storleken på objekt..

Detta är sant i många vardagliga fall, som de som nämndes i början..

Det finns två grundläggande förutsättningar för geometrisk optik:

-Ljuset sprids på ett rätlinjigt sätt.

-Medan de sprider sig genom olika medier gör ljus det enligt empiriska lagar, det vill säga erhållet från experiment.

Grundläggande begrepp inom geometrisk optik

Brytningsindex

Ljusets hastighet i ett materialmedium skiljer sig från ett vakuum. Där vet vi att det är 300 000 km / s, men i luften är det bara lite lägre och ännu mer i vatten eller glas..

Brytningsindex är en dimensionslös mängd, som definieras som kvoten mellan den hastighet med vilken ljus rör sig i vakuum c_eller och hastighet c  i nämnda medium:

n = c_eller / c

Optisk väg

Det är produkten mellan det sträcka som ljuset sträcker sig för att passera från en punkt till en annan, och mediumets brytningsindex:

L = s. n

Där L är den optiska banan är s avståndet mellan de två punkterna och n representerar brytningsindexet, förutsatt konstant.

Med hjälp av den optiska banan jämförs ljusstrålar som rör sig i olika media.

Infallsvinkel

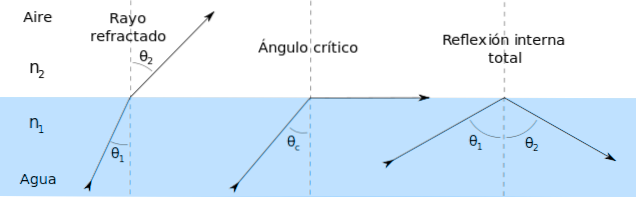
Det är vinkeln som ljusstrålen bildar med den normala linjen mot en yta som skiljer två medier.

Lagar om geometrisk optik

Fermats princip

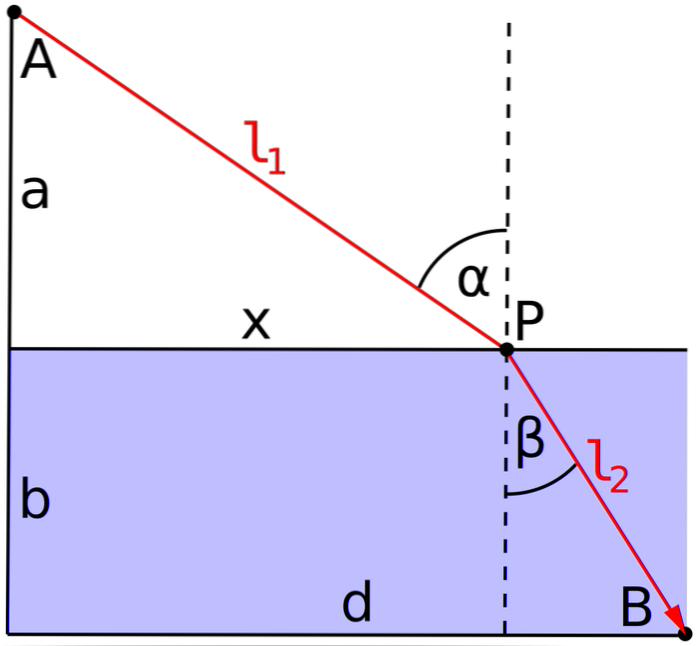
Den franska matematikern Pierre de Fermat (1601-1665) noterade att:

När en ljusstråle rör sig mellan två punkter följer den den väg det tar minsta tid.

Och eftersom ljus rör sig med konstant hastighet måste dess väg vara rätlinjig.

Med andra ord säger Fermats princip att ljusstrålens väg är sådan att den optiska banan mellan två punkter är minimal..

Lag om reflektion

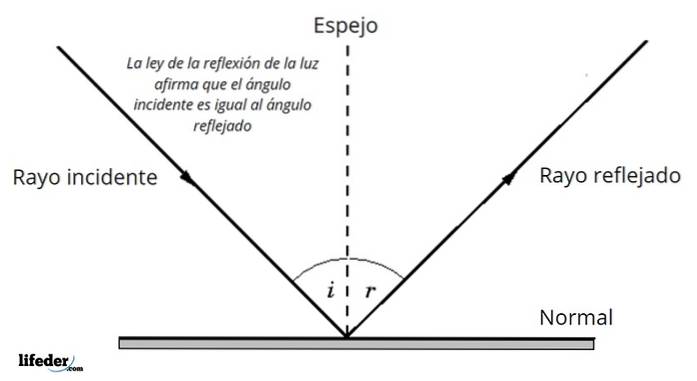
När du träffar ytan som skiljer två olika medier, reflekteras en del av den infallande strålen - eller hela den - tillbaka och gör det med samma uppmätta vinkel i förhållande till det normala mot ytan som den slog med..

Med andra ord är infallsvinkeln lika med reflektionsvinkeln:

 θ_i = θ_{jag '}

Snells lag

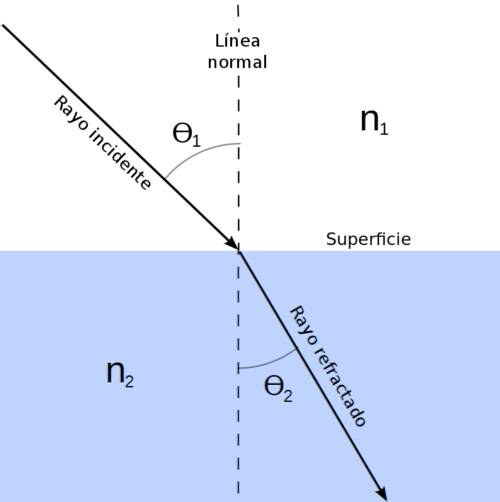
Den holländska matematikern Willebrord Snell (1580-1626) observerade noggrant ljusets beteende när det passerar från luft till vatten och glas.

Han såg att när en ljusstråle faller på ytan som skiljer två medier och bildar en viss vinkel med den, reflekteras en del av strålen tillbaka mot det första mediet och den andra fortsätter sin väg genom det andra..

Således härledde han följande förhållande mellan båda medierna:

n_{1 ⋅} sen θ₁ = n_{2 ⋅} sen θ_två

Var₁ och n_två är respektive brytningsindex, medan θ₁ Y  θ_två  är infallsvinkeln och brytningsvinklarna, mätt med avseende på det normala mot ytan, enligt figuren ovan.

Applikationer

Speglar och linser

Speglar är mycket polerade ytor som reflekterar ljus från föremål, vilket gör att bilder kan bildas. Platta speglar, som de i badrummet eller de som bärs i en handväska, är vanliga.

En lins består av en optisk anordning med två mycket nära brytningsytor. När en stråle av parallella strålar passerar genom en konvergerande lins konvergerar de vid en punkt och bildar en bild. När det gäller en divergerande lins händer det motsatta: strålstrålarna avviker vid en punkt.

Linser används ofta för att korrigera brytningsfel i ögat, liksom i olika optiska förstoringsinstrument..

Optiska instrument

Det finns optiska instrument som gör att bilder kan förstoras, till exempel mikroskop, förstoringsglas och teleskop. Det finns också de som letar över ögonhöjd, som periskop.

Fotokameror används för att ta och bevara bilder som innehåller ett linssystem och ett inspelningselement för att spara den bild som bildas..

Fiberoptisk

Det är ett långt, tunt och transparent material baserat på kiseldioxid eller plast som används för dataöverföring. Det utnyttjar egenskapen för total reflektion: när ljuset når mediet i en viss vinkel inträffar ingen brytning, därför kan strålen färdas långa avstånd och studsar in i glödtråden.

Övningen löst

Objekt längst ner i en pool eller damm verkar vara närmare än de faktiskt är, vilket beror på brytning. På vilket skenbart djup ser en observatör ett mynt som ligger längst ner i en 4 m djup pool??

Antag att strålen som kommer ut ur myntet når observatörens öga i en vinkel på 40 ° i förhållande till det normala..

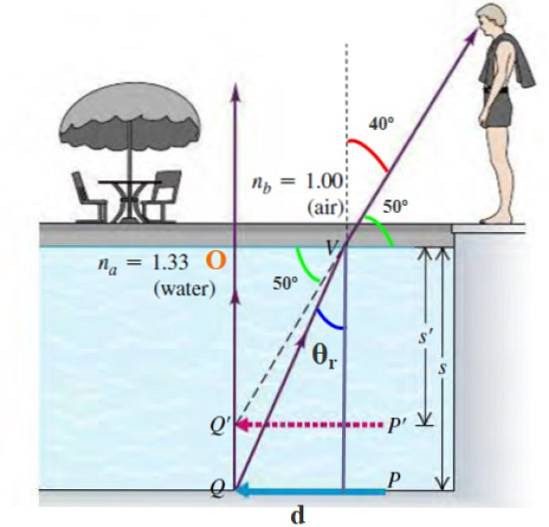
Fakta: brytningsindex för vatten är 1,33, luftens är 1.

Lösning

Det uppenbara djupet på myntet är s och poolens djup är s = 4 m. Myntet är vid punkt Q och observatören ser det vid punkt Q '. Djupet av denna punkt är:

s '= s - Q'Q

Från Snells lag:

n_b ⋅ sin 40º = n_till ⋅ sen θ_r

sen θ_r = (n_b ⋅ sin 40º) ÷ n_till = sin 40º /1,33 = 0,4833

θ_r = arcsen (0,4833) = 28,9º

Genom att känna till denna vinkel beräknar vi avståndet d = OV från höger triangel, vars spetsiga vinkel är θ_r:

solbränna 28,9º = OV / 4 m

OV = 4m × tan 28,9º = 2,154 m

Å andra sidan:

tan 50º = OQ '/ OV

Därför:

OQ '= OV × tan 50º = 2,154 m × tan 50º = 2,57 m.

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 2. Mc Graw Hill.
2. Figueras, M. Geometrisk optik: våglös optik. Öppet universitet i Katalonien.
3. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
4. Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 2. 7: e. Ed. Cengage Learning.
5. Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. Mcgraw hill.