
Vad är procentfelet och hur beräknas det? 10 exempel
De procentuellt fel det är manifestationen av ett relativt fel i procent. Med andra ord är det ett numeriskt fel uttryckt med värdet som ger ett relativt fel, därefter multiplicerat med 100.
För att förstå vad som är ett procentfel är det först viktigt att förstå vad som är ett numeriskt fel, ett absolut fel och ett relativt fel, eftersom procentfelet härrör från dessa två termer.
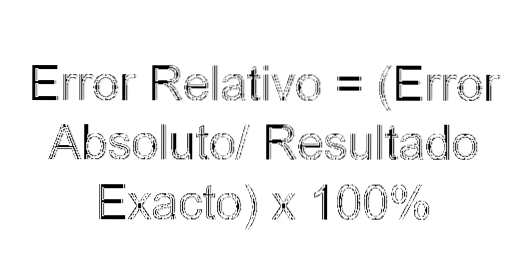
Ett numeriskt fel är ett som visas när en mätning görs på ett otvetydigt sätt när en enhet används (direkt mätning), eller när en matematisk formel används felaktigt (indirekt mätning).
Alla numeriska fel kan uttryckas i absoluta eller procentuella termer. För sin del är det absoluta felet det som härleds när man gör en approximation för att representera en matematisk storlek som härrör från mätningen av ett element eller från felaktig tillämpning av en formel.
På detta sätt ändras det exakta matematiska värdet med approximationen. Beräkningen av det absoluta felet görs genom att subtrahera approximationen från det exakta matematiska värdet, så här:
Absolut fel = Exakt resultat - approximation.
De måttenheter som används för att uttrycka det relativa felet är desamma som de som används för att tala om det numeriska felet. På samma sätt kan detta fel ge ett positivt eller negativt värde.
Det relativa felet är kvoten som erhålls genom att dela det absoluta felet med det exakta matematiska värdet.
På detta sätt är procentfelet det som erhålls genom att multiplicera resultatet av det relativa felet med 100. Med andra ord är procentfelet uttrycket i procent (%) av det relativa felet.
Relativt fel = (absolut fel / exakt resultat)
Ett procentvärde som kan vara negativt eller positivt, det vill säga det kan vara ett överskott eller underrepresenterat värde. Detta värde, till skillnad från det absoluta felet, presenterar inte enheter, utöver procentsatsen (%).
Relativt fel = (absolut fel / exakt resultat) x 100%
Uppdraget för relativa och procentuella fel är att ange kvaliteten på något eller att ge ett jämförande värde.
Exempel på beräkning av procentuella fel
1 - Mätning av två fält
När man mäter två partier eller partier sägs det att det finns cirka 1 m fel i mätningen. En tomt är 300 meter och en annan är 2000.
I detta fall kommer det relativa felet i den första mätningen att vara större än den andra, eftersom i proportion 1 m representerar en högre procentsats i detta fall..
300 m parti:
Ep = (1/300) x 100%
Ep = 0,33%
2000 m parti:
Ep = (1/2000) x 100%
Ep = 0,05%
2 - Mätning av aluminium
Ett aluminiumblock levereras i ett laboratorium. Genom att mäta blockets dimensioner och beräkna dess massa och volym bestäms blockets densitet (2,68 g / cm3).
Men när man granskar nummertabellen för materialet indikerar det att densiteten hos aluminium är 2,7 g / cm3. På detta sätt beräknas absolut- och procentfelet enligt följande:
Ea = 2,7 - 2,68
Ea = 0,02 g / cm3.
Ep = (0,02 / 2,7) x 100%
Ep = 0,74%
3 - Deltagare i ett evenemang
Man antog att 1 000 000 människor skulle gå till en viss händelse. Det exakta antalet personer som deltog i evenemanget var dock 88 000. Det absoluta och procentuella felet skulle vara följande:
Ea = 1 000 000 - 88 000
Ea = 912 000
Ep = (912.000 / 1.000.000) x 100
Ep = 91,2%
4 - Bollfall
Den beräknade tiden det tar för en boll att nå marken efter att ha kastats från ett avstånd på 4 meter är 3 sekunder.
Men vid tidpunkten för experimentet visar man att det tog 2,1 sekunder för bollen att nå marken.
Ea = 3 - 2.1
Ea = 0,9 sekunder
Ep = (0,9 / 2,1) x 100
Ep = 42,8%
5 - Det tar tid för en bil att komma fram
Det är ungefärligt att om en bil går 60 km når den sin destination på 1 timme. Men i verkliga livet tog bilen 1,2 timmar att nå sin destination. Procentfelet för denna tidsberäkning skulle uttryckas enligt följande:
Ea = 1 - 1,2
Ea = -0,2
Ep = (-0,2 / 1,2) x 100
Ep = -16%
6 - Längdmätning
Varje längd mäts med ett värde på 30 cm. När man kontrollerar mätningen av denna längd är det uppenbart att det fanns ett fel på 0,2 cm. Procentandelfelet i detta fall skulle manifestera sig enligt följande:
Ep = (0,2 / 30) x 100
Ep = 0,67%
7 - Broens längd
Beräkningen av broens längd enligt dess planer är 100 m. Men när denna längd bekräftas när den är byggd, visar det sig att den faktiskt är 99,8 m lång. Det procentuella felet skulle bevisas på detta sätt.
Ea = 100 - 99,8
Ea = 0,2 m
Ep = (0,2 / 99,8) x 100
Ep = 0,2%
8 - Diametern på en skruv
Huvudet på en standardtillverkad skruv är 1 cm i diameter.
När man mäter denna diameter observeras dock att skruvhuvudet faktiskt är 0,85 cm. Procentfelet skulle vara följande:
Ea = 1 - 0,85
Ea = 0,15 cm
Ep = (0,15 / 0,85) x 100
Ep = 17,64%
9 - Föremålets vikt
Enligt dess volym och material beräknas vikten på ett visst objekt vara 30 kilo. När objektet har analyserats observeras att dess verkliga vikt är 32 kilo.
I detta fall beskrivs värdet på procentfelet enligt följande:
Ea = 30-32
Ea = -2 kilo
Ep = (2/32) x 100
Ep = 6,25%
10 - Mätning av stål
I ett laboratorium studeras en stålplåt. Genom att mäta arkets mått och beräkna dess massa och volym bestäms arkets densitet (3,51 g / cm3).
När man granskar nummertabellen för materialet indikerar det dock att stålets densitet är 2,85 g / cm3. På detta sätt beräknas absolut- och procentfelet enligt följande:
Ea = 3,51 - 2,85
Ea = 0,66 g / cm3.
Ep = (0,66 / 2,85) x 100%
Ep = 23,15%
Referenser
- Kul, M. i. (2014). Matematik är kul. Erhållen från procentfel: mathsisfun.com
- Helmenstine, A. M. (8 februari 2017). ThoughtCo. Erhållen från hur man beräknar procentfel: thoughtco.com
- Hurtado, A. N., & Sanchez, F. C. (s.f.). Tuxtla Gutiérrez tekniska institut. Erhålls från 1.2 Typer av fel: Absolut fel, relativa fel, procentuella fel, avrundnings- och trunkeringsfel.: Sites.google.com
- Iowa, U. o. (2017). Imaging the Universe. Erhållen från procentfelformel: astro.physics.uiowa.edu
- Lefers, M. (26 juli 2004). Procentfel. Hämtad från definition: groups.molbiosci.northwestern.edu.



Ingen har kommenterat den här artikeln än.