Minskning av liknande villkor (med lösta övningar)

De minskning av liknande villkor är en metod som används för att förenkla algebraiska uttryck. I ett algebraiskt uttryck är liknande termer de som har samma variabel; det vill säga de har samma okända som representeras av en bokstav, och dessa har samma exponenter.

I vissa fall är polynomerna omfattande, och för att nå en lösning måste man försöka minska uttrycket; Detta är möjligt när det finns termer som liknar varandra, som kan kombineras genom att använda operationer och algebraiska egenskaper som addition, subtraktion, multiplikation och division..

Artikelindex

• 1 Förklaring
• 2 Hur man gör en minskning av liknande villkor?
  • 2.1 Exempel
  • 2.2 Minskning av samma termer med lika tecken
  • 2.3 Minskning av liknande termer med olika tecken
• 3 Minskning av liknande villkor i verksamheten
  • 3.1 I summan
  • 3.2 I subtraktion
  • 3.3 I multiplikation
  • 3.4 I divisioner
• 4 Lösta övningar
  • 4.1 Första övningen
  • 4.2 Andra övningen
• 5 Referenser

Förklaring

Liknande termer bildas av samma variabler med samma exponenter, och i vissa fall differentieras dessa bara med sina numeriska koefficienter.

Liknande termer betraktas också som de som inte har variabler; det vill säga de termer som bara har konstanter. Så till exempel är följande liknande termer:

- 6x^två - 3x^två. Båda termerna har samma variabel x^två.

- 4: e^tvåb³ + 2: a^tvåb³. Båda termerna har samma variabler a^tvåb³.

- 7 - 6. Termerna är konstanta.

De termer som har samma variabler men med olika exponenter kallas olika termer, såsom:

- 9a^tvåb + 5ab. Variabler har olika exponenter.

- 5x + och. Variablerna är olika.

- b - 8. En term har en variabel, den andra är en konstant.

Genom att identifiera liknande termer som bildar ett polynom kan dessa reduceras till en, och kombinerar alla de som har samma variabler med samma exponenter. På detta sätt förenklas uttrycket genom att minska antalet termer som komponerar det och beräkningen av dess lösning underlättas..

Hur man gör en minskning av liknande villkor?

Minskningen av liknande villkor görs genom att tillämpa den associerande egenskapen för tillsats och produktens distribuerande egendom. Med hjälp av följande procedur kan du göra en termminskning:

- Liknande termer grupperas först.

- Koefficienterna (siffrorna som åtföljer variablerna) för liknande termer läggs till eller subtraheras, och de associerande, kommutativa eller fördelande egenskaperna tillämpas, i förekommande fall..

- Därefter skrivs de nya termer som erhålls och placerar framför dem tecknet som följd av operationen.

Exempel

Minska termerna för följande uttryck: 10x + 3y + 4x + 5y.

Lösning

Först beställs villkoren för att gruppera de som liknar varandra genom att använda kommutativ egenskap:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Därefter appliceras fördelningsegenskapen och koefficienterna som medföljer variablerna läggs till för att erhålla en minskning av villkoren:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) y

= 14x + 8y.

För att minska lika villkor är det viktigt att ta hänsyn till tecknen på koefficienterna som följer med variabeln. Det finns tre möjliga fall:

Minskning av liknande termer med lika tecken

I detta fall läggs koefficienterna till och villkorstecknet placeras framför resultatet. Därför, om de är positiva, kommer de resulterande villkoren att vara positiva; om villkoren är negativa, kommer resultatet att ha tecknet (-) åtföljd av variabeln. Till exempel:

a) 22ab^två + 12ab^två = 34 ab^två.

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Minskning av liknande villkor cpå olika skyltar

I detta fall subtraheras koefficienterna och tecknet på den största koefficienten placeras framför resultatet. Till exempel:

a) 15x^tvåy - 4x^tvåoch + 6x^tvåy - 11x^tvåY

= (15x^tvåoch + 6x^tvåy) + (- 4x^tvåy - 11x^tvåY)

= 21x^tvåy + (-15x^tvåY)

= 21x^tvåy - 15x^tvåY

= 6x^tvåY.

b) -5a³b + 3 a³b - 4a³b + a³b

= (3 till³b + a³b) + (-5a³b - 4a³b)

= 4a³b - 9a³b

= -5 till³b.

För att reducera liknande termer som har olika tecken bildas en enda tillsatsterm med alla de som har ett positivt tecken (+), koefficienterna läggs till och resultatet åtföljs av variablerna.

På samma sätt bildas en subtraktiv term, med alla de termer som har ett negativt tecken (-) läggs koefficienterna till och resultatet åtföljs av variablerna.

Slutligen subtraheras summan av de två bildade termerna och tecknet på det större placeras från resultatet.

Minskning av liknande villkor i verksamheten

Minskningen av liknande termer är en operation av algebra, som kan användas i tillägg, subtraktion, multiplikation och algebraisk division.

I summor

När du har flera polynom med liknande termer, för att minska dem, ordnas villkoren för varje polynom för att hålla sina tecken, sedan skrivs de en efter en och liknande termer minskas. Till exempel har vi följande polynom:

3x - 4xy + 7x^tvåoch + 5xy^två.

- 6x^tvåy - 2xy + 9 xy^två - 8x.

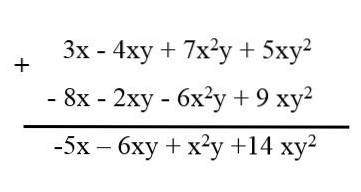
I subtraktion

För att subtrahera ett polynom från ett annat skrivs minuend och subtrend med dess tecken ändras, och sedan görs minskningen av liknande termer. Till exempel:

5: e³ - 3ab^två + 3b^tvåc

6ab^två + 2: a³ - 8b^tvåc

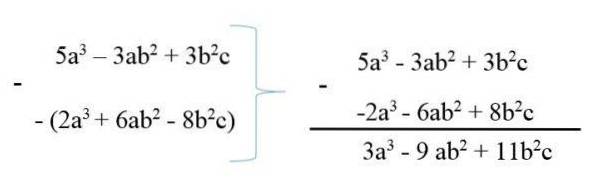
Sålunda sammanfattas polynomerna till 3a³ - 9ab^två + 11b^tvåc.

I multiplikationer

I en produkt av polynom multipliceras termerna som utgör multiplikand med varje term som utgör multiplikatorn, med tanke på att multiplikationens tecken förblir desamma om de är positiva.

De kommer bara att ändras när de multipliceras med en term som är negativ; när två termer av samma tecken multipliceras kommer resultatet att vara positivt (+), och när de har olika tecken blir resultatet negativt (-).

Till exempel:

a) (a + b) _* (a + b)

= a^två + ab + ab + b^två

= a^två + 2ab + b^två.

b) (a + b) _* (a - b)

= a^två - ab + ab - b^två

= a^två - b^två.

cab) _* (a - b)

= a^två - ab - ab + b^två

= a^två - 2ab + b^två.

I divisioner

När du vill minska två polynomer genom en uppdelning måste du hitta ett tredje polynom som, när det multipliceras med det andra (delaren), resulterar i det första polynomet (utdelning).

För det måste villkoren för utdelningen och delaren beställas, från vänster till höger, så att variablerna i båda är i samma ordning.

Sedan genomförs uppdelningen med början från den första terminen till vänster om utdelningen med den första terminen till vänster om delaren, alltid med hänsyn till tecknen på varje term.

Minska till exempel polynom: 10x⁴ - 48x³och + 51x^tvåY^två + 4xy³ - 15 år⁴ dividerar den med polynom: -5x^två + 4xy + 3y^två.

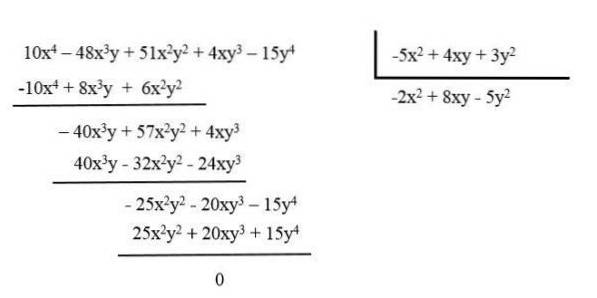
Det resulterande polynomet är -2x^två + 8xy - 5y^två.

Lösta övningar

Första övningen

Minska termerna för det givna algebraiska uttrycket:

15: e^två - 8ab + 6a^två - 6ab - 9 + 4a^två - 13 ab.

Lösning

Den kommutativa egenskapen för addition tillämpas och grupperar termerna som har samma variabler:

15: e^två - 8ab + 6a^två - 6ab + 9 + 4a^två - 13

= (15a^två + 6: e^två + 4: e^två) + (- 8ab - 6ab) + (9 - 13).

Därefter tillämpas multiplikations fördelningsegenskap:

15: e^två - 8ab + 6a^två - 6ab + 9 + 4a^två - 13

= (15 + 6 + 4) a^två + (- 8 - 6) ab + (9 - 13).

Slutligen förenklas de genom att addera och subtrahera koefficienterna för varje term:

15: e^två - 8ab + 6a^två - 6ab + 9 + 4a^två - 13

= 25a^två - 14ab - 4.

Andra övningen

Förenkla produkten av följande polynom:

(8x³ + 7xy^två)_*(8x³ - 7 xy^två).

Lösning

Varje term i det första polynomet multipliceras med det andra, med hänsyn till att tecknen på termerna är olika; därför kommer resultatet av dess multiplikation att bli negativt, liksom exponentlagarna måste tillämpas.

(8x³ + 7xy^två) _* (8x³ - 7xy^två)

= 64 x⁶ - 56 x³_* xy^två + 56 x³_* xy^två - 49 x^tvåY⁴

= 64 x⁶ - 49 x^tvåY⁴.

Referenser

1. Angel, A. R. (2007). Elementär algebra. Pearson Education,.
2. Baldor, A. (1941). Algebra. Havanna: Kultur.
3. Jerome E. Kaufmann, K. L. (2011). Elementär och mellanliggande algebra: en kombinerad strategi. Florida: Cengage Learning.
4. Smith, S. A. (2000). Algebra. Pearson Education.
5. Vigil, C. (2015). Algebra och dess tillämpningar.