
Newtons andra lagansökningar, experiment och övningar
De Newtons andra lag eller dynamikens grundläggande lag fastställer att om ett objekt utsätts för en kraft eller en uppsättning krafter som inte avbryts, kommer objektet att accelerera i den resulterande kraftens riktning, varvid denna acceleration är proportionell mot intensiteten hos den nettokraften och omvänt proportionellt mot objektets massa.
Ja F är nettokraften, M massan av objektet och till den acceleration den får, skulle Newtons andra lag uttryckas matematiskt så här: till = F / M eller på det vanligaste sättet F = M∙till
Artikelindex
- 1 Förklaring och formler
- 2 Lösta övningar
- 2.1 Övning 1
- 2.2 Övning 2
- 3 Tillämpningar av Newtons andra lag
- 3.1 Acceleration av en hiss
- 3.2 Majonnäsburken
- 4 Experiment för barn
- 4.1 Experiment 1
- 4.2 Experiment 2
- 5 Artiklar av intresse
- 6 Referenser
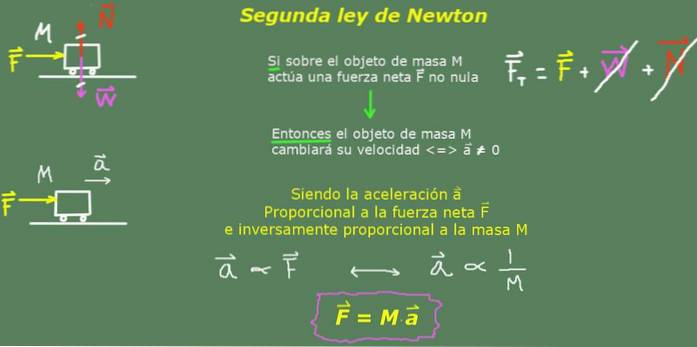
Förklaring och formler
Som förklarats ovan är det vanliga sättet att uttrycka den andra lagen med formeln:
F = M∙till
Både acceleration och kraft måste mätas från en tröghetsreferensram. Observera att massan är en positiv kvantitet, så accelerationen pekar i samma riktning som den resulterande kraften.
Observera också att när den resulterande kraften är noll (F = 0) kommer också accelerationen att vara noll ( till = 0 ) så länge som M> 0. Detta resultat överensstämmer helt med Newtons första lag eller tröghetslag.
Newtons första lag fastställer tröghetsreferenssystem som de som rör sig med konstant hastighet med avseende på en fri partikel. I praktiken och för de vanligaste applikationerna kommer ett referenssystem som är fäst på marken eller något annat som rör sig med konstant hastighet med avseende på det att betraktas som tröghet..
Kraft är det matematiska uttrycket för objektets interaktion med miljön. Kraften kan vara en konstant mängd eller förändras med tiden, positionen och hastigheten på objektet..
Enheten i det internationella systemet (SI) för styrka är Newton (N). Massan i (SI) mäts i (kg) och accelerationen i (m / s)två). En kraft Newton är den kraft som krävs för att accelerera ett objekt med massa 1 kg vid 1 m / stvå .
Lösta övningar
Övning 1
Ett massföremål m frigörs från en viss höjd och en fallacceleration på 9,8 m / s² mäts.
Detsamma händer med ett annat objekt med massa m 'och ett annat av massa m "och ett annat och ett annat. Resultatet är alltid tyngdacceleration som betecknas med g och är lika med 9,8 m / s². I dessa experiment är formen på objektet och dess massa är sådant att kraften på grund av luftmotstånd är försumbar.
Det ombeds att hitta en modell för jordens attraktiva kraft (känd som vikt) som överensstämmer med de experimentella resultaten..
Lösning
Vi väljer ett tröghetsreferenssystem (fast i förhållande till marken) med en positiv riktning av den vertikala X-axeln och nedåt.
Den enda kraften som verkar på massföremålet m är jordens attraktion, den kraften kallas vikten P, hur det pekar ner är positivt.
Acceleration som massobjektet förvärvar m när det släpps är det a = g , påpekad och positiv.
Vi föreslår Newtons andra lag
P = m a
Vad kommer att vara modellen för P så att accelerationen som förutses av den andra lagen är g oavsett värdet på m? : Det enda alternativet är att P = m g när m> 0.
m g = m a varifrån vi rensar: a = g
Vi drar slutsatsen att vikten, den kraft med vilken jorden drar till sig ett objekt, kommer att vara objektets massa multiplicerad med tyngdacceleration och dess riktning är vertikal och pekar nedåt.
P = m∙g
Övning 2
Ett block på 2 kg massa vilar på ett helt plant och horisontellt golv. Om en kraft på 1 N appliceras på den, vad är blockets acceleration och vilken hastighet det kommer att ha efter 1 s.
Lösning
Det första är att definiera ett tröghets koordinatsystem. En har valts med X-axeln på golvet och Y-axeln vinkelrät mot den. Sedan skapas ett kraftdiagram som placerar krafterna på grund av blockets interaktioner med dess omgivning.

Kraften N representerar det normala, det är den vertikala uppåtgående kraften som golvytan utövar på blocket M. Det är känt att N exakt balanserar P eftersom blocket inte rör sig i vertikal riktning.
F är den horisontella kraften som appliceras på block M och pekar i X-axelns positiva riktning.
Nettokraften är summan av alla krafter på massblocket M. Vi gör vektorsumman av F, P och N. Eftersom P och N är lika och motsatta, annullerar de varandra och nettokraften är F.
Så den resulterande accelerationen blir kvoten av nettokraften och massan:
a = F / M = 1 N / 2 kg = 0,5 m / s ^
När blocket börjar från vila efter 1s kommer dess hastighet att ändras från 0 m / s till 0,5 m / s .
Tillämpningar av Newtons andra lag
Påskynda en hiss
En pojke använder en badrumsvåg för att mäta sin vikt. Det värde du får är 50 kg. Sedan tar pojken vikten till hissen i sin byggnad, för han vill mäta hissens acceleration. Resultaten som erhålls vid start är:
- Vågen registrerar en vikt på 58 kg i 1,5 s
- Mät sedan 50 kg igen.
Med dessa data beräknar du hissens acceleration och hastigheten den får.
Lösning
Skalan mäter vikten i en enhet som kallas kilogram_styrka. Per definition är kilogram_kraften den kraft med vilken planeten Jorden drar till sig ett objekt med massa 1 kg.
När den enda kraften som verkar på objektet är dess vikt, får den en acceleration på 9,8 m / s². Så 1 kg_f är lika med 9,8 N.
Vikten P av pojken är då 50 kg * 9,8 m / s² = 490 N
Under acceleration utövar vågen en kraft N på pojken på 58 kg_f motsvarande 58 kg * 9,8 m / s² = 568,4 N.
Hissens acceleration kommer att ges av:
a = N / M - g = 568,4 N / 50 kg - 9,8 m / s² = 1,57 m / s²
Hastigheten förvärvad av hissen efter 1,5 s med acceleration av 1,57 m / s² är:
v = a * t = 1,57 m / s² * 1,5 s = 2,36 m / s = 8,5 Km / h
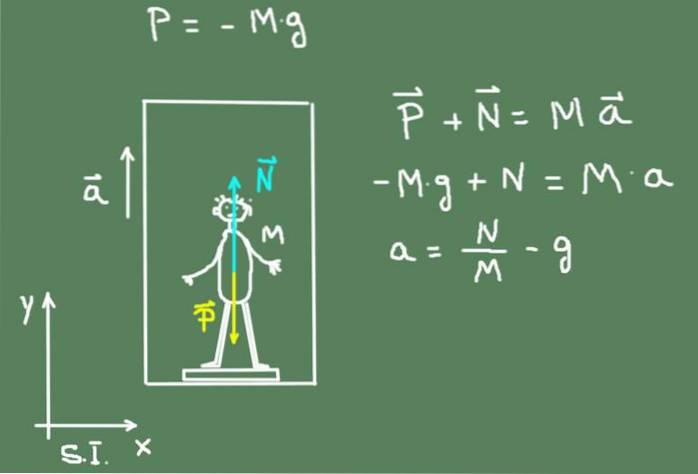
Följande bild visar ett diagram över de krafter som verkar på pojken:
Majonnäsburken
En pojke lämnar sin bror burken majonnäs till sin bror, som är i andra änden av bordet. För det driver den den på ett sådant sätt att den får en hastighet på 3 m / s. Från det ögonblick som flaskan släpptes tills den stannade i motsatta änden av bordet var resan 1,5 m.
Bestäm värdet på den friktionskraft som bordet utövar på flaskan, med vetskap om att den har en massa på 0,45 kg.
Lösning
Först bestämmer vi bromsacceleration. För detta kommer vi att använda följande förhållande, redan känt från den enhetligt accelererade rätlinjiga rörelsen:
Vf² = Vi² + 2 * a * d
var Vf är sluthastigheten, Fick syn på ursprungliga hastigheten, till acceleration och d förskjutningen.
Acceleration som erhållits från det tidigare förhållandet är, där förskjutningen av flaskan har tagits som positiv.
a = (0 - 9 (m / s) ²) / (2 * 1,5 m) = -3 m / s²
Nettokraften på majonnäsburken är friktionskraften, eftersom burkens normala vikt och vikt: Fnet = Fr.
Fr = m * a = 0,45 kg * (-3 m / s²) = -1,35 N = -0,14 kg-f
Experiment för barn
Barn och vuxna kan utföra enkla experiment som gör det möjligt för dem att verifiera att Newtons andra lag verkligen fungerar i verkligheten. Här är två mycket intressanta:
Experiment 1
Ett enkelt experiment kräver en badrumsvåg och en hiss. Ta en badrumsvikt i en hiss och registrera de värden som den markerar under uppstart, nedstart och under tiden du rör dig med konstant hastighet. Beräkna hissaccelerationerna för varje fall.
Experiment 2
- Ta en leksaksbil som har sina smorda hjul
- Fäst ett rep till slutet.
- Tejpa en penna eller annat slätt, cylindriskt föremål över vilket strängen passerar vid kanten av bordet..
- Häng en liten korg i den andra änden av repet, där du placerar några mynt eller något som fungerar som vikt..
Schemat för experimentet visas nedan:
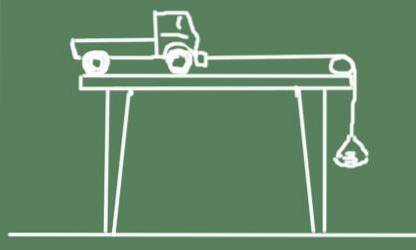
- Släpp vagnen och se hur den påskyndas.
- Öka sedan vagnens massa genom att placera mynt på den, eller något som ökar dess massa..
- Säg om accelerationen ökar eller minskar. Lägg mer deg på vagnen, se hur den accelererar och avsluta.
Vagnen lämnas sedan utan extra vikt och får accelerera. Mer vikt läggs sedan på korgen för att öka kraften som appliceras på vagnen..
- Jämför accelerationen med föregående fall, ange om den ökar eller minskar. Du kan upprepa att lägga till mer vikt i korgen och observera accelerationen i vagnen.
- Ange om den ökar eller minskar.
- Analysera dina resultat och säg om de överensstämmer med Newtons andra lag.
Artiklar av intresse
Exempel på Newtons andra lag.
Newtons första lag.
Exempel på Newtons andra lag.
Referenser
- Alonso M., Finn E. 1970. Fysikvolym I: Mekanik. Interamerikansk utbildningsfond S.A. 156-163.
- Hewitt, P. 2012. Konceptuell fysik. Femte upplagan. 41-46.
- Young, Hugh. 2015. Universitetsfysik med modern fysik. 14: e utgåvan Pearson. 108-115.



Ingen har kommenterat den här artikeln än.