
Halvcirkel hur man beräknar omkrets, area, centroid, övningar
De halvcirkel är en plan figur avgränsad av en diameter på omkretsen och en av de två plana cirkelbågarna bestämda av diametern.
På detta sätt gränsar en halvcirkel till en halvcirkel, som består av en platt cirkelbåge och ett rakt segment som förenar ändarna av den plana cirkelbågen. Halvcirkeln omfattar halvcirkeln och alla punkter inuti den..
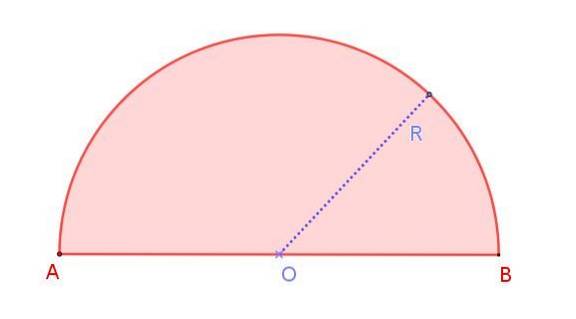
Vi kan se detta i figur 1, som visar en halvcirkel med radien R, vars mått är hälften av diametern AB. Observera att till skillnad från en cirkel där det finns oändliga diametrar finns det bara en diameter i halvomkretsen.
Halvcirkeln är en geometrisk figur med många användningsområden inom arkitektur och design, som vi ser i följande bild:

Artikelindex
- 1 Element och mått på en halvcirkel
- 1.1 Halvcirkelns omkrets
- 1.2 Område för en halvcirkel
- 1.3 Centroid av en halvcirkel
- 1.4 Tröghetsmoment för en halvcirkel
- 1.5 Inskriven vinkel
- 2 Lösta övningar
- 2.1 Övning 1
- 2.2 Övning 2
- 2.3 Övning 3
- 2.4 Övning 4
- 2.5 Övning 5
- 3 Referenser
Element och mått på en halvcirkel
Elementen i en halvcirkel är:
1.- Den plana cirkelbågen A⌒B
2.- Segmentet [AB]
3.- Punkterna inuti halvcirkeln som består av bågen A⌒B och segmentet [AB].
Halvcirkelns omkrets
Omkretsen är summan av bågens kontur plus den för det raka segmentet, därför:
Perimeter = båglängd A⌒B + segmentlängd [AB]
I fallet med en halvcirkel med radien R kommer dess omkrets P att ges med formeln:
P = π⋅R + 2⋅R = (π + 2) ⋅R
Den första termen är halva omkretsen av en cirkel med radie R, medan den andra är längden på diametern, vilket är dubbelt så stor som radien..
Område av en halvcirkel
Eftersom en halvcirkel är en av de plana vinkelsektorerna som förblir när man drar en diameter genom omkretsen, kommer dess område A att vara halva arean av cirkeln som innehåller halvcirkeln med radien R:
A = (π⋅Rtvå) / 2 = ½ π⋅Rtvå
Centroid av en halvcirkel
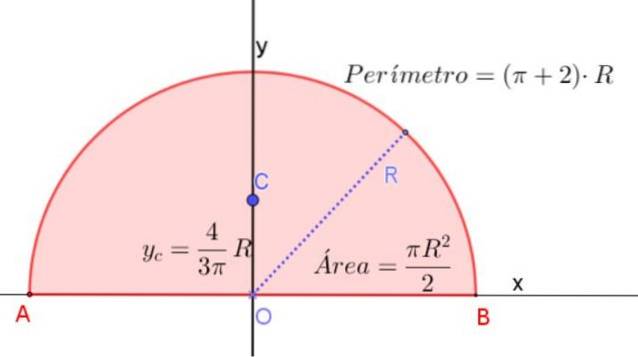
Halvcirkelns centrum är på sin symmetriaxel på en höjd uppmätt från dess diameter 4 / (3π) gånger radien R.
Detta motsvarar ungefär 0,424⋅R, mätt från mitten av halvcirkeln och på dess symmetriaxel, som visas i figur 3.
Tröghetsmoment för en halvcirkel
Tröghetsmomentet för en plan figur i förhållande till en axel, till exempel x-axeln, definieras som:
Integralen av kvadraten för avståndet från de punkter som tillhör figuren till axeln, integrationsdifferensen är ett oändligt minimalt element, tagen vid positionen för varje punkt.
Figur 4 visar definitionen av tröghetsmomentet Ix av halvcirkeln med radien R, med avseende på X-axeln som passerar genom dess diagonal:
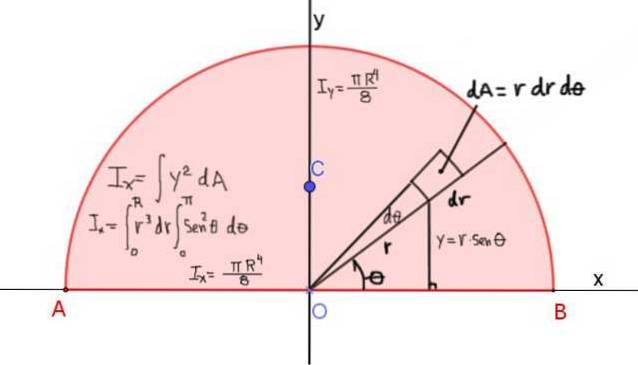
Tröghetsmomentet kring x-axeln ges av:
Jagx = (π⋅R4) / 8
Och tröghetsmomentet med avseende på symmetriaxeln y är:
Iy = (π⋅R4) / 8
Det noteras att båda tröghetsmomenten sammanfaller i sin formel, men det är viktigt att notera att de hänvisar till olika axlar.
Inskriven vinkel
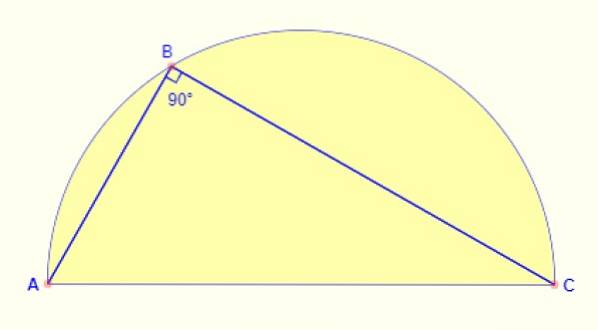
Vinkeln inskriven i halvcirkeln är alltid 90º. Oavsett var punkten tas på bågen är vinkeln mellan sidorna AB och BC i figuren alltid rätt..
Lösta övningar
Övning 1
Bestäm omkretsen av en halvcirkel med en radie av 10 cm.
Lösning
Kom ihåg att omkretsen som en funktion av radien ges av formeln vi såg tidigare:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Övning 2
Hitta området för en halvcirkel med en radie av 10 cm.
Lösning
Formeln för området för en halvcirkel är:
A = ½ π⋅Rtvå = ½ π⋅ (10 cm)två = 50π cmtvå = 50 x 3,14 cmtvå = 157 cmtvå.
Övning 3
Bestäm höjden h för centroid för en halvcirkel med radie R = 10 cm mätt från dess bas, och halvcirkelns diameter är densamma.
Lösning
Centroid är halvcirkelns jämviktspunkt och dess position är på symmetriaxeln på en höjd h från basen (halvcirkelns diameter):
h = (4⋅R) / (3π) = (410 cm) / (3 x 3,14) = 4,246 cm
Övning 4
Hitta tröghetsmomentet för en halvcirkel i förhållande till axeln som sammanfaller med dess diameter, med vetskap om att halvcirkeln är gjord av ett tunt ark. Dess radie är 10 cm och dess massa är 100 gram.
Lösning
Formeln som ger tröghetsmomentet för halvcirkeln är:
Jagx = (π⋅R4) / 8
Men eftersom problemet berättar för oss att det är en materiell halvcirkel, måste den tidigare relationen multipliceras med ytdensiteten för halvcirkelns massa, som kommer att betecknas med σ.
Jagx = σ (π⋅R4) / 8
Vi fortsätter sedan med att bestämma σ, vilket inte är något annat än halvcirkelns massa dividerat med dess område.
Området bestämdes i övning 2 och resultatet var 157 cmtvå. Då blir ytdensiteten för denna halvcirkel:
σ = 100 gram / 157 cmtvå = 0,637 g / cmtvå
Då beräknas tröghetsmomentet med avseende på diametern så här:
Jagx = (0,637 g / cmtvå) [3,1416 ⋅ (10 cm)4] / 8
Resulterande:
Jagx = 2502 g⋅cmtvå
Övning 5
Bestäm tröghetsmomentet för en halvcirkel med en radie av 10 cm gjord av ett materialark med en ytdensitet på 0,637 g / cmtvå längs en axel som passerar genom dess centrum och är parallell med dess diameter.
Lösning
För att lösa denna övning är det nödvändigt att komma ihåg Steiners sats om tröghetsmoment för parallella axlar, som säger:
Tröghetsmomentet I med avseende på en axel som ligger på ett avstånd h från centroiden är lika med summan av tröghetsmomentet Ic med avseende på en axel som passerar genom centroid och är parallell med den första plus produkten av massan gånger kvadraten för separationen av de två axlarna.
Jag = jagc + M htvå
I vårt fall är jag känd vilket är tröghetsmomentet med avseende på diametern, som redan var beräknad i övning 4. Separationen h mellan diametern och centroid är också känd, vilken beräknades i övning 3.
Vi behöver bara rensa Ic:
Jagc = I - M htvå
Jagc = 2502 g⋅cmtvå - 100g 4.2 (4,246 cm)två vilket ger som resultat att tröghetsmomentet genom en axel parallell med diametern och passerar genom centroid är:
Jagc = 699,15 g⋅cmtvå
Referenser
- Alexander, D. 2013. Geometri. 5: e. Utgåva. Cengage Learning.
- Math Open Reference. Halvcirkel. Återställd från: mathopenref.com.
- Universum Formler Halvcirkel. Återställd från: universoformulas.com.
- Universumsformler. Område för en halvcirkel. Återställd från: universoformulas.com.
- Wikipedia. Halvcirkel. Återställd från: en.wikipedia.com.

Ingen har kommenterat den här artikeln än.