Torrsubstanser med volym, typer, lösta övningar

De solid av revolution Det är den tredimensionella figuren som genereras genom att rotera en plan yta runt den axiella axeln eller rotationsaxeln. Figur 1 visar en animering av ett revolutionärt material genererat på detta sätt.

Ett annat mycket lätt att visualisera exempel består i att generera en höger cirkulär cylinder, rotera en rektangel med höjd eller längd h och radie r, runt den positiva x-axeln (figur 2). För att hitta volymen finns en välkänd formel:

V = area av bas x höjd

Andra revolutionära fasta ämnen är sfären, den högra cirkulära konen och olika figurer, beroende på ytan som roteras och naturligtvis den valda axeln..

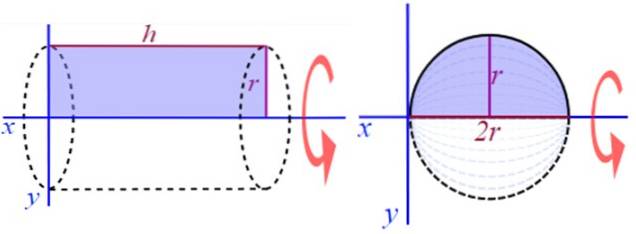
Om du till exempel roterar halvcirkeln runt en linje som är parallell med diametern, får den en ihålig rotation.

För cylindern, konen, sfären, både fast och ihålig, finns det formler för att hitta volymen, vilket beror på radien och höjden. Men när de genereras av andra ytor beräknas volymen med bestämda integraler.

Artikelindex

• 1 Typer av fasta partiklar
  • 1.1 Sfär
  • 1.2 Kon
  • 1.3 Cylinder
  • 1.4 Toroid
• 2 Metoder för att beräkna volymen av en fast substans av revolution
  • 2.1 Skiv- eller brickmetod
  • 2.2 Skiktmetod
• 3 Övningen löst
• 4 Referenser

Typer av revolutionära fasta ämnen

Revolutionens fasta ämnen kan klassificeras enligt kurvan som genererar dem:

Sfär

Det räcker att rotera en halvcirkel runt en axel som kommer att vara diametern på sfären med radie R. Dess volym är:

V_sfär = (4/3) πR³

Kon

För att få en kon med höjd H och radie R är ytan som ska roteras en rätt triangel, runt den axiella axeln som passerar genom ett av benen. Dess volym är:

V_kon = (1/3) πHR^två

Cylinder

Genom att rotera en rektangel runt en axiell axel som passerar genom en av sidorna, vilket kan vara kortsidan eller långsidan, får vi en rätt cirkulär cylinder med radie R och höjd H, vars volym är:

V_cylinder = πR^tvåH

Toroid

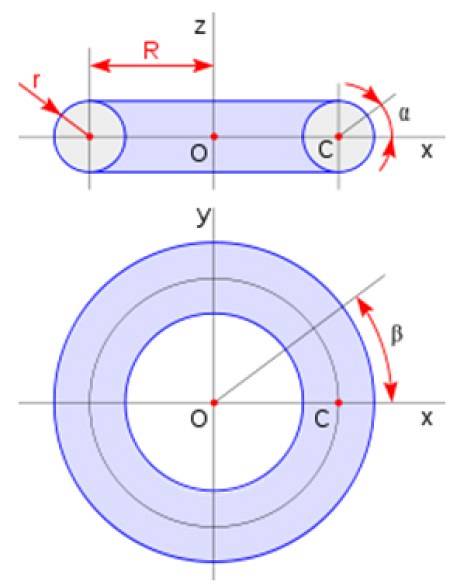
Torus är formad som en munk. Det erhålls genom att rotera ett cirkulärt område runt en linje i planet som inte skär varandra. Dess volym ges av:

V_torus = 2πa^tvåR

Där a är tvärsnittsradien och R är torusradien enligt schemat som visas i figuren:

Metoder för att beräkna volymen av en fasta revolution

I integrerad beräkning är dessa två metoder vanliga:

-Skivor och brickor

-Skal

Skiva- eller tvättmetod

Vid skärning av en fast revolution kan tvärsnittet vara en skiva, om den är solid, eller det kan vara en slags bricka (en skiva med ett hål i mitten), om det är ett ihåligt fast ämne..

Antag att en plan region roteras runt den horisontella axeln. Från detta plana område tar vi en liten rektangel med bredden Δx, som roteras vinkelrätt runt den axiella axeln.

Rektangelns höjd är mellan den yttersta kurvan R (x) och den innersta kurvan r (x). De motsvarar den yttre respektive inre radien..

Genom att göra denna rotation genereras en tvättmaskin med volym AV, ges av:

ΔV = Full volym - hålvolym (om någon)

Kom ihåg att volymen på en höger cirkulär cylinder är π. radio^två x höjd, vi har:

AV = π [R^två(x) - r^två(x)] Ax

Det fasta ämnet kan delas in i en mängd små volymdelar AV. Om vi ​​lägger till dem alla har vi full volym.

För att göra detta gör vi att volymen AV tenderar till 0, med vilken Δx också blir mycket liten och blir en differentiell dx.

Så vi har en integral:

V = ∫_till^b π [R^två(x) - r^två(x)] dx

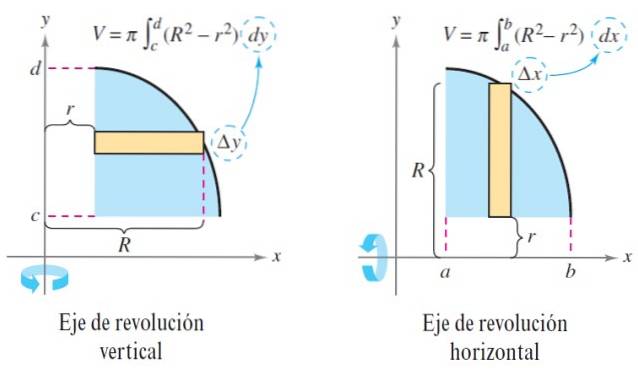
Om det fasta materialet är fast, är funktionen r (x) = 0, den skiva av det fasta som genereras är en skiva och volymen förblir:

V = ∫_till^b πR^två(x) dx

När rotationsaxeln är vertikal har ovanstående ekvationer formen:

V = ∫_till^b π [R^två (y) - r^två (y)] dy y V = ∫_till^b πR^två(y) dy

Skiktmetod

Som namnet antyder består denna metod i att anta att det fasta ämnet består av skikt med olika tjocklek. Skiktet är ett tunt rör som härrör från rotationen av en rektangel parallellt med rotationsaxeln.

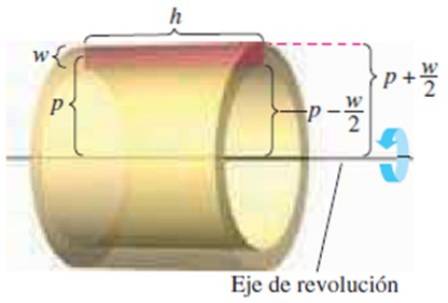
Vi har följande dimensioner:

-Rektangelns höjd w

-Dess longitud h

-Avståndet från mitten av rektangeln till rotationsaxeln sid

Att veta att skiktets volym är yttre volym - inre volym:

π (p + w / 2)^tvåh - π (p - w / 2)^tvåh

Genom att utveckla anmärkningsvärda produkter och förenkla får du:

Skiktvolym = 2π⋅p⋅w⋅h

Låt oss nu göra höjden w för rektangeln Ay, som framgår av följande bild:

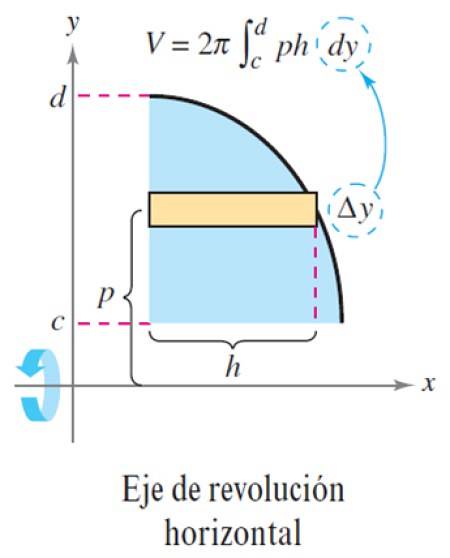
Med detta är volymen AV:

AV = 2π p x h x Ay

Och göra antalet lager n är mycket stor, Δy blir en differentiell dy, med vilken den totala volymen är integralen:

V = ∫_c^d 2π p (y) h (y) dy

Det beskrivna förfarandet gäller på samma sätt när rotationsaxeln är vertikal:

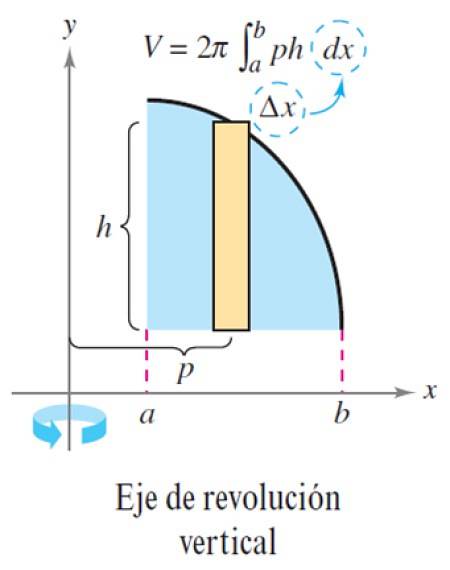
Övningen löst

Hitta volymen som genereras av rotation av planområdet mellan kurvorna:

y = x^två;  y = 0; x = 2

Runt y-axeln.

Lösning

-Det första vi måste göra är att kartlägga regionen som kommer att generera den fasta revolutionen och ange rotationsaxeln. Vi har det i följande graf:

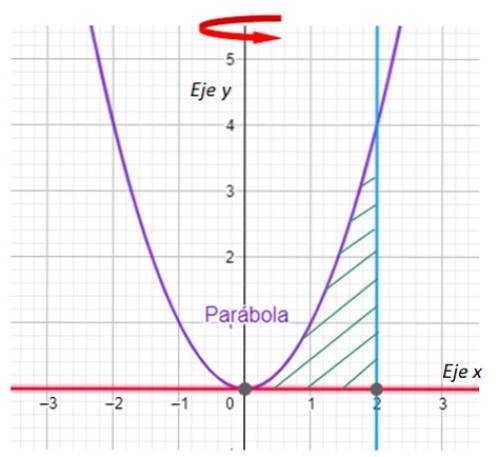
-Nu letar vi efter korsningarna mellan kurvan y = x^två och linjen x = 2. För sin del är linjen y = 0 ingen annan än x-axeln.

Från diagrammet är det lätt att se att parabolen och linjen skär varandra vid punkten (2,4), vilket bekräftas genom att ersätta x = 2 i y = x^två.

-Sedan väljs en av metoderna för att beräkna volymen, till exempel skiktmetoden med vertikal rotationsaxel:

V = ∫_till^b 2π p (x) h (x) dx

Steg 1: Rita rektangeln

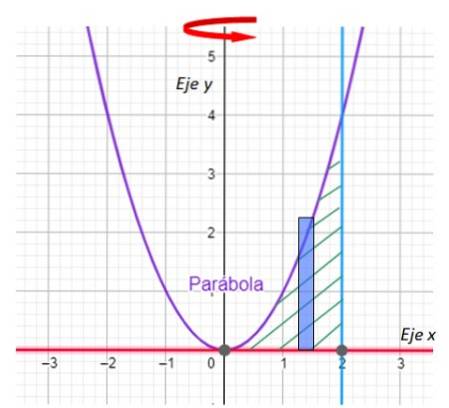
Viktig: I skiktningsmetoden är rektangelns långsida parallell med rotationsaxeln.

Steg 2: Bestäm p (x)

Skiktets radie är x

Steg 3: bestäm h (x)

Rektangelns höjd bestäms av parabolen x^två.

Steg 4: fastställa och lösa volymintegralen

Integrationsvariabeln är x, som varierar mellan 0 och 2, med detta har vi gränserna för integration. Ersätta uttrycken för p (x) och h (x)

Referenser

1. Larson, R. 2010. Beräkning av en variabel. 9: e. Utgåva. Mcgraw hill.
2. Purcell, E. 2007. Kalkyl med analytisk geometri. 9: e. Utgåva. Pearson Education.
3. Wikipedia. Solid av revolutionen. Återställd från: en.wikipedia.org.
4. Wikipedia. Toroid Återställd från: es.wikipedia.org.
5. Wolfram MathWorld. Solid av revolutionen. Återställd från: mathworld.wolfram.com.