
Molekylär kinetisk teorihistoria, postulat och exempel

De molekylär kinetisk teori Det är en som försöker förklara de experimentella observationerna av gaser ur ett mikroskopiskt perspektiv. Det vill säga det försöker associera naturen och beteendet hos de gasformiga partiklarna med de fysiska egenskaperna hos gasen som en vätska; förklara det makroskopiska från det mikroskopiska.
Gaser har alltid varit av intresse för forskare på grund av deras egenskaper. De upptar hela volymen av behållaren i vilken de finns, och kan komprimeras helt utan att deras innehåll motsätter sig minst motstånd; och om temperaturen ökar börjar behållaren expandera och kan till och med spricka.
Många av dessa egenskaper och beteenden sammanfattas i de ideala gaslagarna. De betraktar emellertid gasen som en helhet och inte som en samling av miljontals partiklar utspridda i rymden; Dessutom tillhandahåller den inte, baserat på tryck, volym och temperaturdata, ytterligare information om hur dessa partiklar rör sig.
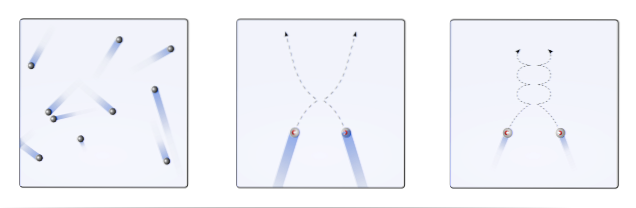
Det är alltså då som den molekylära kinetiska teorin (TCM) föreslår att de visualiseras som mobila sfärer (övre bild). Dessa sfärer kolliderar med varandra och väggarna godtyckligt och upprätthåller en linjär bana. Men när temperaturen sjunker och trycket ökar blir sfärernas böjning böjd..
En gas, enligt TCM, ska bete sig som sfärerna i bildens första ram. Men genom att kyla ner och öka trycket på dem är deras beteende långt ifrån idealiskt. De är då verkliga gaser, nära att genomgå flytande och övergår därmed till vätskefasen.
Under dessa förhållanden blir samspelet mellan sfärerna viktigare, så långt att deras hastigheter avtar tillfälligt. Ju närmare de är flytande, desto mer kurviga blir deras banor (infällda till höger), och desto mindre energiska blir deras kollisioner..
Artikelindex
- 1 Historia
- 1.1 Daniel Bernoulli
- 1.2 Rudolf Clausius
- 1.3 James Clerk Maxwell och Ludwig Boltzmann
- 2 Postulat av molekylär kinetisk teori
- 2.1 Volymen på gasformiga partiklar är försumbar
- 2.2 Attraktionskrafterna mellan partiklarna är noll
- 2.3 Gasformiga partiklar är alltid i rörelse
- 2.4 Kollisioner mellan partiklar och behållarväggar är elastiska
- 2.5 Kinetisk energi förblir inte konstant
- 2.6 Medel kinetisk energi är lika med en given temperatur för alla gaser
- 3 Exempel
- 3.1 Boyles lag
- 3.2 Karls lag
- 3.3 Daltons lag
- 4 Referenser
Berättelse
Daniel Bernoulli
Idén om dessa sfärer, bättre kallade atomer, hade redan övervägs av den romerska filosofen Lucretius; inte för gaser, utan för fasta, statiska föremål. Å andra sidan tillämpade Daniel Bernoulli 1738 atomvisionen på gaser och vätskor genom att föreställa sig dem som orubbliga sfärer som rör sig i alla riktningar..
Hans arbete stred dock mot fysikens lagar vid den tiden; en kropp kunde inte röra sig evigt, så det var omöjligt att tro att en uppsättning atomer och molekyler skulle kollidera med varandra utan att förlora sin energi; det vill säga att förekomsten av elastiska kollisioner inte var möjligt.
Rudolf clausius
Ett sekel senare förstärkte andra författare TCM med en modell där de gasformiga partiklarna rörde sig bara i en riktning. Rudolf Clausius sammanställde emellertid sina resultat och sammanställde en mer komplett TCM-modell med vilken han försökte förklara de ideala gaslagar som demonstrerades av Boyle, Charles, Dalton och Avogadro..
James Clerk Maxwell och Ludwig Boltzmann
1859 förklarade James Clerk Maxwell att gasformiga partiklar uppvisar ett hastighetsområde vid en given temperatur och att en uppsättning av dem kan övervägas med hjälp av en genomsnittlig molekylhastighet..
Sedan 1871 kopplade Ludwig Boltzmann befintliga idéer med entropi, och hur gas termodynamiskt alltid tenderar att uppta så mycket utrymme som möjligt homogent och spontant.
Postulat av molekylär kinetisk teori
För att ta hänsyn till gasen från dess partiklar är en modell nödvändig där vissa postulat eller antaganden uppfylls. postulerar som logiskt sett måste kunna förutsäga och förklara (så exakt som möjligt) makroskopiska och experimentella observationer. Med detta sagt nämns och beskrivs TCM-postulaten.
Volymen av de gasformiga partiklarna är försumbar
I en behållare fylld med gasformiga partiklar sprids dessa och rör sig bort från varandra i alla hörn. Om de för ett ögonblick alla kunde samlas vid en viss punkt i behållaren utan kondensering, skulle det observeras att de endast upptar en försumbar del av behållarens volym..
Det betyder att behållaren, även om den innehåller miljoner gasformiga partiklar, faktiskt är mer tom än full (volym-tomrumsförhållande mycket mindre än 1); om dess barriärer tillåter det kan det och gasen inuti det komprimeras plötsligt; eftersom i slutet av dagen är partiklarna mycket små, liksom deras volym.
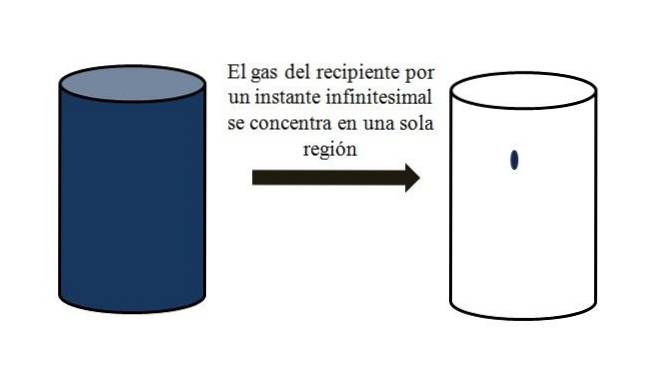
Den övre bilden illustrerar exakt ovanstående med en blåfärgad gas.
De attraktiva krafterna mellan partiklarna är noll
De gasformiga partiklarna inuti behållaren kolliderar med varandra utan tillräckligt med tid för att deras interaktioner ska få styrka; ännu mindre när det som huvudsakligen omger dem är molekylärt vakuum. En omedelbar konsekvens av detta är att deras linjära vägar tillåter dem att helt omfatta behållarens volym..
Om detta inte var fallet skulle en behållare med en "bisarr" och "labyrintisk" form ha fuktiga områden som ett resultat av gaskondens; istället färdas partiklarna runt behållaren med full frihet utan att kraften i deras interaktioner hindrar dem.
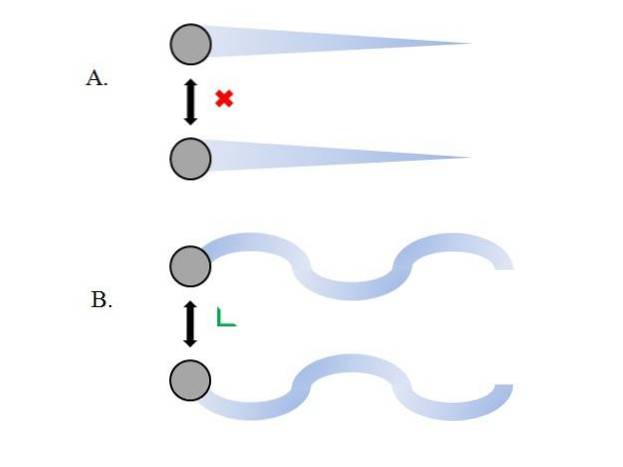
De linjära banorna i den övre bilden (A.) visar detta postulat; medan om banorna är böjda (B.), visar det att det finns interaktioner som inte kan ignoreras mellan partiklarna.
Gasformiga partiklar är alltid i rörelse
Från de två första postulaten konvergerar också det faktum att gaspartiklarna aldrig slutar röra sig. När de väl är suddiga i behållaren kolliderar de med varandra och med dess väggar, med en kraft och hastighet som är direkt proportionell mot den absoluta temperaturen; denna kraft är, tryck.
Om de gasformiga partiklarna slutade röra sig ett ögonblick skulle "röktungar" bevittnas inuti behållaren, som dyker upp från ingenstans, med tillräckligt med tid för att ordna sig i vakuum och ge slumpmässiga former..
Kollisioner mellan partiklarna och behållarens väggar är elastiska
Om bara elastiska kollisioner mellan de gasformiga partiklarna och behållarens väggar dominerar inuti behållaren kommer kondens av gasen aldrig att inträffa (så länge de fysiska förhållandena inte förändras); eller vad är detsamma som att säga att de aldrig vilar och alltid kolliderar.
Detta beror på att i elastiska kollisioner finns det ingen nettoförlust av kinetisk energi; en partikel kolliderar med väggen och studsar i samma hastighet. Om en partikel när den kolliderar saktar ner accelererar den andra utan att producera värme eller ljud som sprider kinetisk energi hos någon av dem.
Kinetisk energi förblir inte konstant
Partiklarnas rörelse är slumpmässig och kaotisk, så att de inte alla har samma hastighet; precis som det händer, till exempel på en motorväg eller i en folkmassa. Vissa är mer energiska och reser snabbare, medan andra är långsamma och väntar på en kollision för att påskynda dem.
För att beskriva dess hastighet är det då nödvändigt att beräkna ett genomsnitt; och med detta erhålles den genomsnittliga kinetiska energin för de gasformiga partiklarna eller molekylerna i tur och ordning. Eftersom den kinetiska energin för alla partiklar ständigt förändras tillåter medelvärdet bättre kontroll av data och kan bearbetas med större tillförlitlighet..
Genomsnittlig kinetisk energi är lika med en given temperatur för alla gaser
Genomsnittlig molekylär kinetisk energi (ECsmp) i en behållare förändras med temperaturen. Ju högre temperatur, desto högre blir energin. Eftersom det är ett genomsnitt kan det finnas partiklar eller gaser som har högre eller lägre energi än detta värde; några snabbare respektive andra långsammare.
Matematiskt kan det visas att ECsmp det beror uteslutande på temperaturen. Det betyder att oavsett vad gasen är, dess massa eller molekylära struktur, dess ECsmp den kommer att vara densamma vid temperaturen T och varierar bara om den ökar eller minskar. Av alla postulat är detta kanske det mest relevanta..
Och hur är det med den genomsnittliga molekylhastigheten? Till skillnad från EGsmp, molekylmassan påverkar hastigheten. Ju tyngre den gasformiga partikeln eller molekylen, är det naturligt att förvänta sig att den rör sig långsammare..
Exempel
Här är några korta exempel på hur TCM har lyckats förklara de ideala gaslagarna. Även om det inte behandlas kan andra fenomen, såsom gasdiffusion och effusion, också förklaras med TCM.
Boyles lag
Om behållarens volym komprimeras vid konstant temperatur minskar avståndet som de gasformiga partiklarna måste resa för att kollidera med väggarna. vilket är lika med en ökning av frekvensen av sådana kollisioner, vilket resulterar i större tryck. Eftersom temperaturen förblir konstant, ECsmp det är också konstant.
Charles Law
Om du ökar T, ECsmp kommer att öka. De gasformiga partiklarna rör sig snabbare och kolliderar ett större antal gånger med behållarens väggar; så trycket ökar.
Om väggarna är flexibla och kan expandera kommer deras yta att bli större och trycket kommer att sjunka tills det blir konstant. och som ett resultat kommer volymen också att öka.
Daltons lag
Om flera liter olika gaser tillsattes en rymlig behållare, som kommer från mindre behållare, skulle dess totala inre tryck vara lika med summan av det partiella trycket som utövas av varje gastyp separat..
Varför? Eftersom alla gaser börjar kollidera med varandra och spridas homogent; interaktionerna mellan dem är noll och vakuumet dominerar i behållaren (TCM-postulat), så det är som om varje gas var ensam och utövar sitt tryck individuellt utan interferens från andra gaser.
Referenser
- Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan). CENGAGE Learning, P 426-431.
- Fernandez Pablo. (2019). Molekylär kinetisk teori. Vix. Återställd från: vix.com
- Jones, Andrew Zimmerman. (7 februari 2019). Kinetic Molecular Theory of Gases. Återställd från: thoughtco.com
- Hall Nancy. (5 maj 2015). Kinetisk teori om gaser. Glenn Research Center. Återställd från: grc.nasa.gov
- Blaber M. & Lower S. (09 oktober 2018). Grunderna i kinetisk molekylär teori. Kemi LibreTexts. Återställd från: chem.libretexts.org
- Den kinetiska molekylära teorin. Återställd från: chemed.chem.purdue.edu
- Wikipedia. (2019). Kinetisk teori om gaser. Återställd från: en.wikipedia.org
- Toppr. (s.f.). Kinetisk molekylär teori om gaser. Återställd från: toppr.com


Ingen har kommenterat den här artikeln än.