
Bayes teoremförklaring, tillämpningar, övningar
De Bayes sats är ett förfarande som gör det möjligt för oss att uttrycka den villkorliga sannolikheten för en slumpmässig händelse A given B, i termer av sannolikhetsfördelningen för händelse B given A och sannolikhetsfördelningen för endast A.
Denna sats är mycket användbar, eftersom tack vare den kan vi relatera sannolikheten för att en händelse A inträffar med vetskap om att B inträffade, med sannolikheten att det motsatta inträffar, det vill säga att B inträffar med.
Bayes sats var ett silverförslag av pastor Thomas Bayes, en engelsk teolog från 1700-talet som också var matematiker. Han var författare till flera verk inom teologin, men för närvarande är han känd för ett par matematiska avhandlingar, bland vilka den redan nämnda Bayes-satsen sticker ut som huvudresultatet.
Bayes behandlade denna teorem i ett arbete med titeln "En uppsats för att lösa ett problem i lärandens chanser", som publicerades 1763, och som ett stort antal har utvecklats. Studier med tillämpningar inom olika kunskapsområden.
Artikelindex
- 1 Förklaring
- 2 Tillämpningar av Bayes sats
- 2.1 Lösta övningar
- 3 Referenser
Förklaring
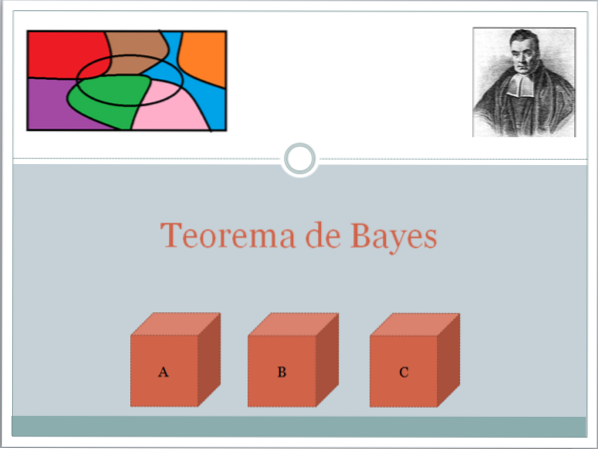
För det första, för en bättre förståelse av denna teorem, är några grundläggande begrepp om sannolikhetsteori nödvändiga, särskilt multiplikationsteorem för villkorlig sannolikhet, som säger att
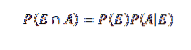
För E och A godtyckliga händelser i ett provutrymme S.
Och definitionen av partitioner, som säger att om vi har A1 ,TILLtvå,..., TILLn händelser i ett provutrymme S, kommer dessa att bilda en partition av S, om Ai är ömsesidigt exklusiva och deras förening är S.
Med tanke på detta, låt B vara en annan händelse. Så vi kan se B som
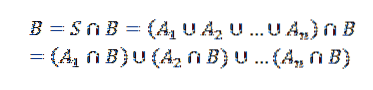
Där Ai korsade med B är ömsesidigt exklusiva händelser.
Och i konsekvens,
Använd sedan multiplikationssatsen
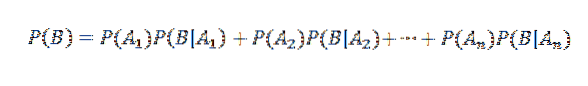
Å andra sidan definieras den villkorliga sannolikheten för Ai givet B av
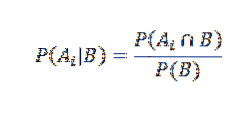
Att ersätta på rätt sätt har vi det för alla i
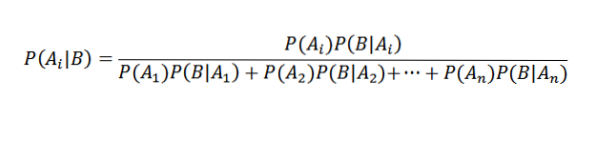
Tillämpningar av Bayes sats
Tack vare detta resultat har forskargrupper och olika företag lyckats förbättra kunskapsbaserade system..
I studien av sjukdomar kan Bayes-satsen till exempel hjälpa till att urskilja sannolikheten för att en sjukdom finns i en grupp människor med en viss egenskap och ta som data de globala hastigheterna för sjukdomen och dominansen av nämnda egenskaper i båda friska och sjuka människor.
Å andra sidan har det i högteknologivärlden påverkat stora företag som tack vare detta resultat har utvecklat "kunskapsbaserad" programvara.
Som ett dagligt exempel har vi Microsoft Office-assistenten. Bayes sats hjälper mjukvaran att utvärdera de problem som användaren presenterar och avgöra vilka råd som ska tillhandahållas och därmed kunna erbjuda en bättre tjänst enligt användarens vanor..
Det bör noteras att denna formel ignorerades fram till nyligen, detta beror främst på att när detta resultat utvecklades för 200 år sedan fanns det lite praktisk användning för dem. Men i vår tid, tack vare stora tekniska framsteg, har forskare hittat sätt att omsätta detta resultat i praktiken.
Lösta övningar
Övning 1
Ett mobiltelefonföretag har två maskiner A och B. 54% av de mobiltelefoner som tillverkas tillverkas av maskin A och resten av maskin B. Inte alla tillverkade mobiltelefoner är i gott skick.
Andelen defekta mobiltelefoner från A är 0,2 och av B är 0,5. Vad är sannolikheten för att en mobiltelefon från fabriken är defekt? Vad är sannolikheten att den kommer från maskin A, med vetskap om att en mobiltelefon är defekt,?
Lösning
Här har du ett experiment som utförs i två delar; i den första delen inträffar händelserna:
A: cell tillverkad av maskin A.
B: cell tillverkad av maskin B.
Eftersom maskin A producerar 54% av mobiltelefoner och resten produceras av maskin B, följer att maskin B producerar 46% av mobiltelefoner. Sannolikheten för dessa händelser anges, nämligen:
P (A) = 0,54.
P (B) = 0,46.
Händelserna i den andra delen av experimentet är:
D: defekt mobiltelefon.
E: icke-defekt mobiltelefon.
Som anges i uttalandet beror sannolikheten för dessa händelser på resultatet som erhållits i första delen:
P (D | A) = 0,2.
P (D | B) = 0,5.
Med hjälp av dessa värden kan sannolikheten för komplementen till dessa händelser också bestämmas, det vill säga:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Nu kan händelse D skrivas enligt följande:
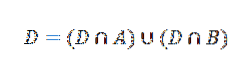
Använda multiplikationssatsen för resultat av villkorlig sannolikhet:
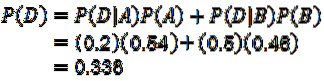
Med vilken den första frågan besvaras.
Nu behöver vi bara beräkna P (A | D), för vilken Bayes-satsen tillämpas:
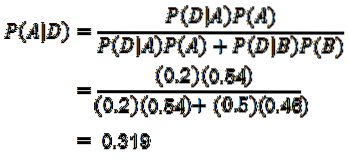
Tack vare Bayes sats kan det konstateras att sannolikheten att en mobiltelefon har gjorts av maskin A, med vetskap om att mobiltelefonen är defekt, är 0,319.
Övning 2
Tre lådor innehåller svarta och vita bollar. Sammansättningen av var och en av dem är som följer: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
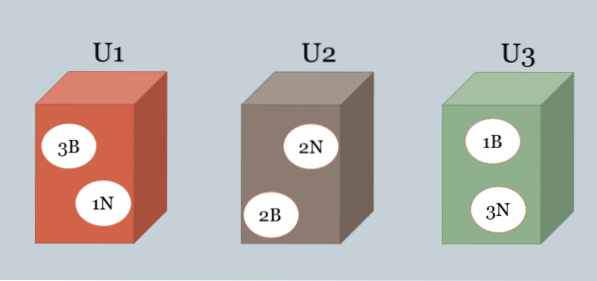
En av rutorna väljs slumpmässigt och en boll dras slumpmässigt som visar sig vara vit. Vilken är rutan som troligen har valts?
Lösning
Med U1, U2 och U3 representerar vi också den valda rutan.
Dessa händelser utgör en partition av S och det verifieras att P (U1) = P (U2) = P (U3) = 1/3 eftersom valet av rutan är slumpmässigt.
Om B = den dragna bollen är vit har vi P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Vad vi vill erhålla är sannolikheten att bollen har tagits ur lådan Ui med vetskap om att bollen var vit, det vill säga P (Ui | B), och se vilken av de tre värdena som var högst att veta av vilken ruta har troligen varit utvinningen av den vita bollen.
Tillämpa Bayes sats på den första rutan:
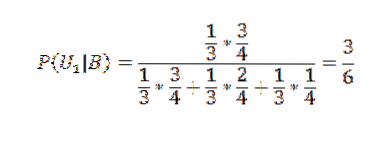
Och för de andra två:
P (U2 | B) = 2/6 och P (U3 | B) = 1/6.
Sedan är den första av lådorna den med högsta sannolikhet att ha valts för utvinning av den vita kulan..
Referenser
- Kai Lai Chung. Elementär möjlighetsteori med stokastiska processer. Springer-Verlag New York Inc.
- Kenneth H. Rosen. Diskret matematik och dess tillämpningar. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannolikhet och statistiska tillämpningar. S.A. MEXIKANSKA ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Lösta problem med diskret matematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori och sannolikhetsproblem. McGRAW-HILL.



Ingen har kommenterat den här artikeln än.