
Nortons satsbeskrivning, tillämpningar, exempel och övningar
De Nortons teorem, som appliceras på elektriska kretsar, fastställer att en linjär krets med två anslutningar a och b kan ersättas med en helt likvärdig, som består av en strömkälla som heter IInte ansluten parallellt med ett motstånd RInte.
Sagt nuvarande jagInte Jag hördeN Det är den som skulle flyta mellan punkterna a och b om de kortsluts. Motståndet RN är motsvarande motstånd mellan terminalerna när alla oberoende källor stängs av. Allt som sägs beskrivs i figur 1.

Den svarta rutan i figuren innehåller den linjära kretsen som ska ersättas med dess Norton-motsvarighet. En linjär krets är en där ingången och utgången har ett linjärt beroende, såsom förhållandet mellan spänningen V och likströmmen I ett ohmiskt element: V = I.R.
Detta uttryck motsvarar Ohms lag, där R är motståndet, vilket också kan vara en impedans, om det är en växelströmskrets.
Nortons teorem utvecklades av elingenjören och uppfinnaren Edward L. Norton (1898-1983), som arbetade länge för Bell Labs..
Artikelindex
- 1 Tillämpningar av Nortons teorem
- 1.1 Förhållandet mellan Norton och Thevenin satser
- 2 Exempel
- 3 Övningen löst
- 4 Referenser
Tillämpningar av Nortons teorem
När du har mycket komplicerade nätverk, med många motstånd eller impedanser och du vill beräkna spänningen mellan någon av dem, eller strömmen som strömmar genom den, förenklar Nortons teorem beräkningarna, eftersom som vi har sett kan nätverket ersättas med en mindre och mer hanterbar krets.
På detta sätt är Nortons teorem mycket viktigt när man utformar kretsar med flera element, samt att studera deras svar..
Förhållandet mellan Norton och Thevenin-satser
Nortons sats är den dubbla av Thevenins sats, vilket innebär att de är likvärdiga. Thevenins sats indikerar att den svarta rutan i figur 1 kan ersättas av en spänningskälla i serie med ett motstånd, kallat Thevenin-motståndet RTh. Detta uttrycks i följande figur:
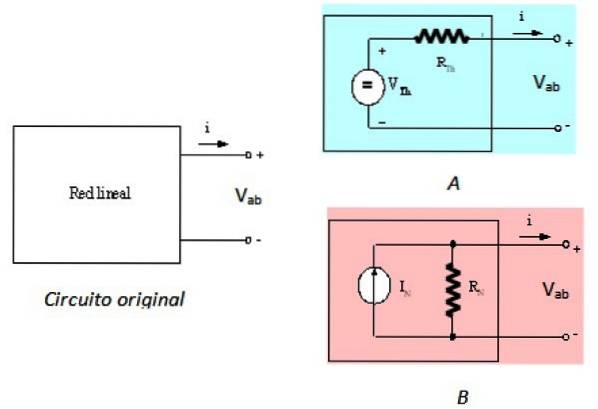
Kretsen till vänster är den ursprungliga kretsen, det linjära nätverket i den svarta rutan, krets A längst upp till höger är Thevenin-ekvivalenten och kretsen B det är Norton-ekvivalenten, som beskrivs. Sett från terminalerna a och b är de tre kretsarna ekvivalenta.
Observera nu att:
-I den ursprungliga kretsen är spänningen mellan terminalerna V.ab.
-Vab = VTh i kretsen TILL
-Slutligen Vab = JagN.RN i kretsen B
Om klämmorna a och b är kortslutna i alla tre kretsarna måste man vara övertygad om att spänningen och strömmen mellan dessa punkter måste vara densamma för alla tre, eftersom de är ekvivalenta. Sedan:
-I den ursprungliga kretsen är strömmen i.
-För krets A är strömmen i = V.Th / RTh, enligt Ohms lag.
-Slutligen i krets B är strömmen IN
Därför dras slutsatsen att motstånden mellan Norton och Thevenin har samma värde, och att strömmen ges av:
jag = jagN = VTh / RTh = VTh / RN
Exempel
För att korrekt tillämpa Nortons teorem följs följande steg:
-Isoler från nätverket den sektion av kretsen för vilken Norton-ekvivalenten finns.
-Ange terminalerna a och b i den återstående kretsen.
-Ersätt spänningskällorna för kortslutningar och strömkällorna för öppna kretsar för att hitta motsvarande motstånd mellan plintarna a och b. Det här är RN.
-Återställ alla källor till sina ursprungliga positioner, kortslutningsklämmorna a och b och hitta strömmen som flyter mellan dem. Detta är jagN.
-Rita Norton-ekvivalentkretsen enligt vad som anges i figur 1. Både strömkällan och motsvarande motstånd är parallella.
Du kan också använda Thevenins teorem för att hitta RTh, som vi redan vet är lika med RN, sedan enligt Ohms lag kan du hitta jagN och fortsätt att rita den resulterande kretsen.
Och nu ska vi se ett exempel:
Hitta Norton-ekvivalenten mellan punkterna A och B i följande krets:
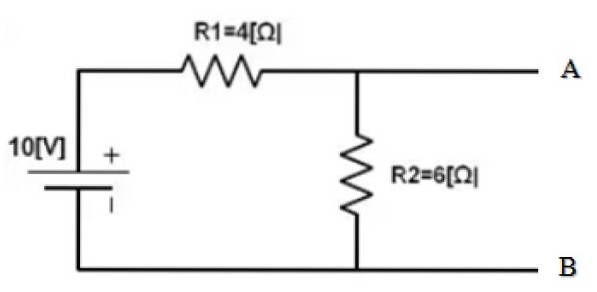
Den del av kretsen vars ekvivalent är att hitta är redan isolerad. Och punkterna A och B är tydligt bestämda. Följande är att kortsluta 10 V-källan och hitta motsvarande motstånd för den erhållna kretsen:
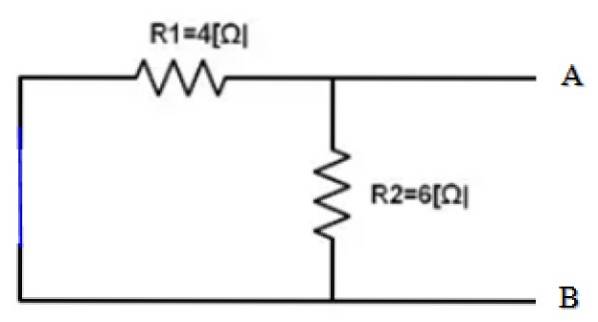
Utsikt från terminal A och B, båda motstånden R1 och Rtvå är parallella, därför:
1 / Rekv = 1 / R12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → Rekv = 12/5 Ω = 2,4 Ω
Då returneras källan till sin plats och punkterna A och B kortsluts för att hitta strömmen som cirkulerar där, det här är jagN. Isåfall:
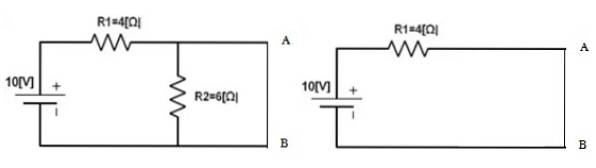
JagN = 10 V / 4 Ω = 2,5 A.
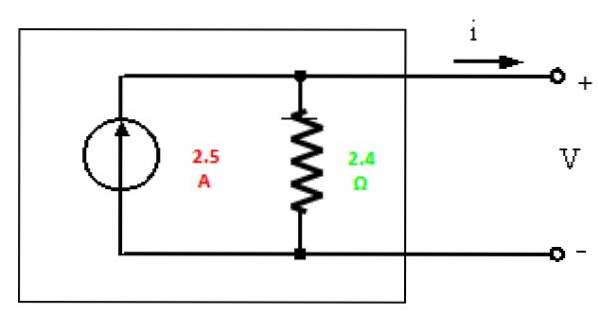
Norton motsvarande
Slutligen ritas Norton-ekvivalenten med de hittade värdena:
Övningen löst
I kretsen enligt följande bild:
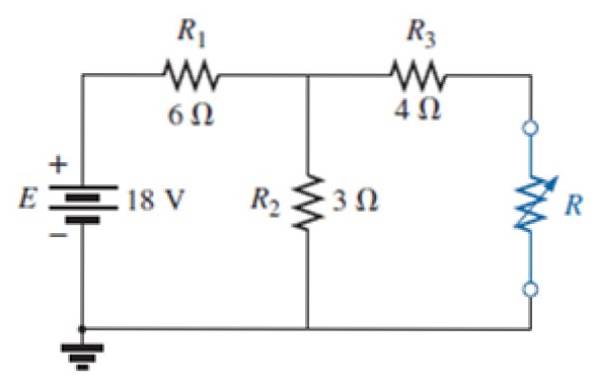
a) Hitta Norton-ekvivalentkretsen för det externa nätverket till det blå motståndet.
b) Hitta även motsvarigheten till Thévenin.
Lösning till
Följ stegen ovan, källan måste kortslutas:
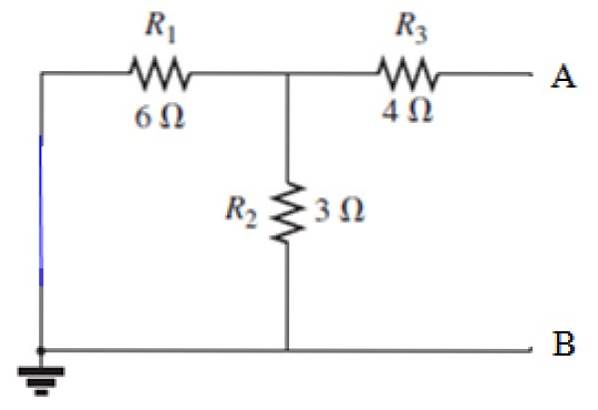
Beräkning av RN
Vy från plint A och B, motstånd R3 är i serie med parallellen bildad av motstånden R1 och Rtvå, låt oss först beräkna motsvarande motstånd för denna parallell:
1 / R12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → Rekv = 2/1 Ω = 2Ω
Och sedan är denna parallell i serie med R3, så att motsvarande motstånd är:
Rekv = 2 Ω + 4 Ω = 6 Ω
Detta är värdet på båda RN från RTh, som förklarats tidigare.
IN beräkning
Terminalerna A och B kortsluts sedan och returnerar källan till sin plats:
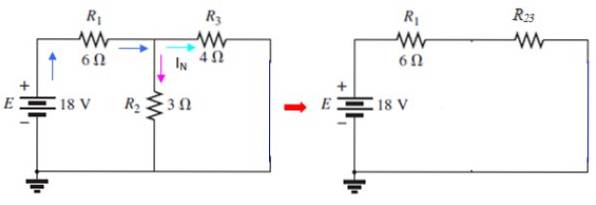
Strömmen genom jag3 är det nuvarande jagN som kan bestämmas med hjälp av nätmetoden eller med serie och parallell. I denna krets Rtvå och R3 är parallella:
1 / R2. 3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R2. 3 = 12/7 Ω
Motståndet R1 är i serie med denna parallell, då:
R123 = 6 + (12/7) Ω = 54/7 Ω
Strömmen som lämnar källan (blå färg) beräknas med hjälp av Ohms lag:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A
Denna ström är uppdelad i två delar: en som passerar genom Rtvå och en annan som passerar R3. Strömmen genom parallell R2. 3 det är detsamma som går igenom R1, som visas i mellankretsen i figuren. Spänningen där är:
V2. 3 = I.R2. 3 = (7/3) A. (12/7) Ω = 4 V
Båda motstånden Rtvå och R3 är vid den spänningen, eftersom de är parallella, därför:
Jag3 = V2. 3 / R3 = 4 V / 4 Ω = 1 A.
Vi har redan sökt efter Norton-strömmen eftersom jag som tidigare sagt3 = JagN, sedan:
JagN = 1 A.
Norton motsvarande
Allt är klart för att rita Norton-ekvivalenten för denna krets mellan punkterna A och B:
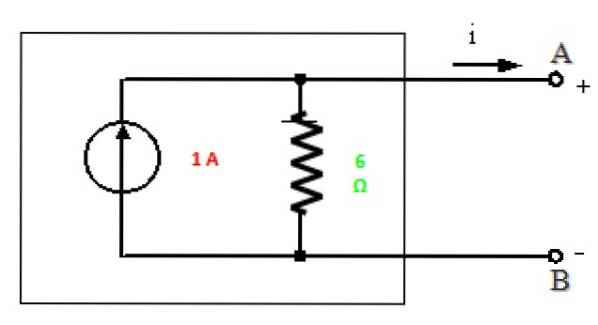
Lösning b
Att hitta Thévenin-ekvivalenten är väldigt enkelt, eftersom RTh = RN= 6 Ω och som förklarats i föregående avsnitt:
VTh = JagN. RN = 1 A. 6 Ω = 6 V
Thévenins ekvivalenta krets är:
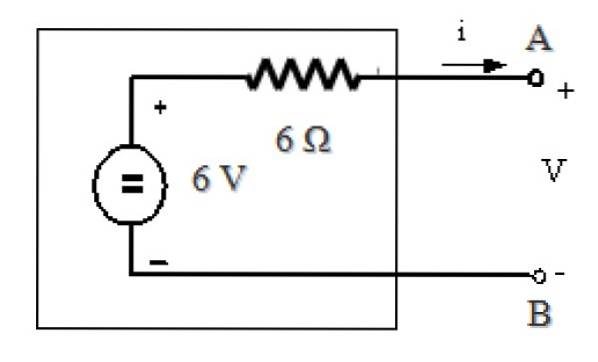
Referenser
- Alexander, C. 2006. Grundläggande för elektriska kretsar. 3: e. Utgåva. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion till kretsanalys. 2: a. Utgåva. Pearson.
- Dorf, R. 2006. Introduktion till elektriska kretsar. 7: e. Utgåva. John Wiley & Sons.
- Edminister, J. 1996. Elektriska kretsar. Schaum-serien. 3: e. Utgåva. Mc Graw Hill.
- Wikipedia. Nortons teorem. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.