
Torricellis sats vad den består av, formler och övningar
De Torricellis sats Torricelli-principen säger att hastigheten för vätskan som kommer ut genom hålet i en tank eller behållares vägg är identisk med hastigheten för ett föremål som får falla fritt från en höjd som är lika med vätskans fria yta upp till hålet.
Satsen illustreras i följande bild:
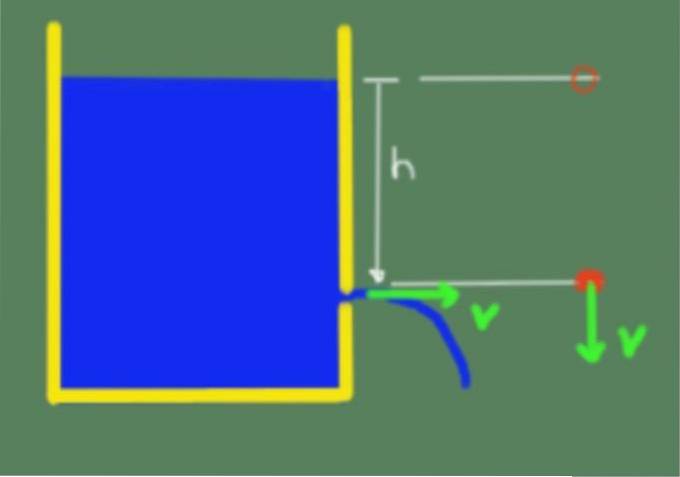
På grund av Torricellis teorem kan vi sedan bekräfta att vätskans utgångshastighet genom en öppning som är i höjd h under vätskans fria yta ges med följande formel:
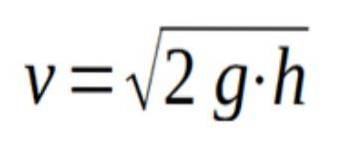
Där g är tyngdaccelereringen och h är höjden från hålet till vätskans fria yta.
Evangelista Torricelli var en fysiker och matematiker född i staden Faenza, Italien 1608. Torricelli krediteras uppfinningen av kvicksilverbarometern och i erkännande finns det en tryckenhet som kallas ”torr”, motsvarande en millimeter kvicksilver (mm Hg).
Artikelindex
- 1 Bevis på satsen
- 1.1 Fallande föremål
- 1.2 Vätska kommer ut ur hålet
- 2 Lösta övningar
- 2.1 Övning 1
- 3 I) Det lilla utloppsröret till en vattentank är 3 m under vattenytan. Beräkna utloppshastigheten för vattnet.
- 3.1 Övning 2
- 3.2 Övning 3
- 4 Referenser
Bevis på satsen
I Torricellis sats och i formeln som ger hastigheten antar den att viskositetsförlusterna är försumbara, precis som i fritt fall antas att friktionen på grund av luften som omger det fallande föremålet är försumbar..
Ovanstående antagande är rimligt i de flesta fall och innebär också bevarande av mekanisk energi.
För att bevisa satsen hittar vi först formeln för hastigheten för ett objekt som släpps med noll initialhastighet, från samma höjd som vätskeytan i tanken..
Principen för energibesparing kommer att tillämpas för att uppnå det fallande föremålets hastighet precis när det har sjunkit ner en höjd h lika med det från hål till fri yta.
Eftersom det inte finns några friktionsförluster är det giltigt att tillämpa principen för bevarande av mekanisk energi. Antag att det fallande föremålet har massa m och höjden h mäts från vätskans utgångsnivå.
Fallande föremål
När föremålet frigörs från en höjd som är lika med vätskans fria yta, är dess energi endast gravitationspotential, eftersom dess hastighet är noll och därför är dess kinetiska energi noll. Den potentiella energin Ep ges av:
Ep = m g h
När den passerar framför hålet är dess höjd noll, då är den potentiella energin noll, så den har bara kinetisk energi Ec ges av:
Ec = ½ m vtvå
Eftersom energin bevaras Ep = Ec från vad som erhålls:
½ m vtvå = m g h
Lösa för hastighet v Torricelli-formeln erhålls sedan:
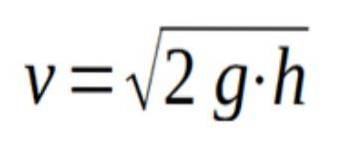
Vätska kommer ut ur hålet
Därefter hittar vi vätskans utgångshastighet genom hålet för att visa att den sammanfaller med det som just beräknades för ett fritt fallande föremål.
För detta kommer vi att basera oss på Bernoullis princip, som inte är något annat än bevarande av energi som appliceras på vätskor.
Bernoullis princip formuleras så här:
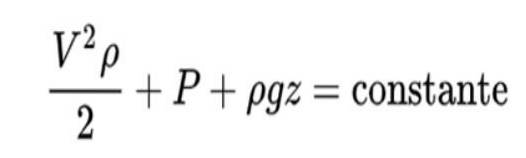
Tolkningen av denna formel är som följer:
- Den första termen representerar vätskans kinetiska energi per volymenhet
- Den andra representerar arbetet utfört av tryck per tvärsnittsareaenhet.
- Den tredje representerar gravitationspotentialenergin per volymenhet vätska..
När vi utgår ifrån att det är en idealisk vätska, i icke-turbulenta förhållanden med relativt låga hastigheter, är det relevant att bekräfta att den mekaniska energin per volymenhet i fluiden är konstant i alla områden eller tvärsnitt av samma..
I denna formel V är vätskans hastighet, ρ vätskans densitet, P tryck och z vertikal position.
Figuren nedan visar Torricelli-formeln med utgångspunkt från Bernoullis princip.
Vi använder Bernoullis formel på den fria ytan av vätskan betecknad med (1) och på utgångshålet betecknad med (2). Nollhuvudnivån har valts jämnt med utloppshålet.
Under förutsättningen att tvärsnittet i (1) är mycket större än i (2), kan vi sedan anta att vätskans nedstigningshastighet i (1) är praktiskt taget försumbar.
Det är därför V1= 0, det tryck som vätskan utsätts för i (1) är atmosfärstryck och höjden uppmätt från öppningen är h.
För utloppssektionen (2) antar vi att utloppshastigheten är v, det tryck som vätskan utsätts för vid utloppet är också atmosfärstryck och utloppshöjden är noll.
Värdena som motsvarar avsnitten (1) och (2) ersätts i Bernoullis formel och sätts lika. Jämställdheten gäller eftersom vi antar att vätskan är idealisk och att det inte finns några viskösa friktionsförluster. När alla termer har förenklats erhålls hastigheten vid utgångshålet.
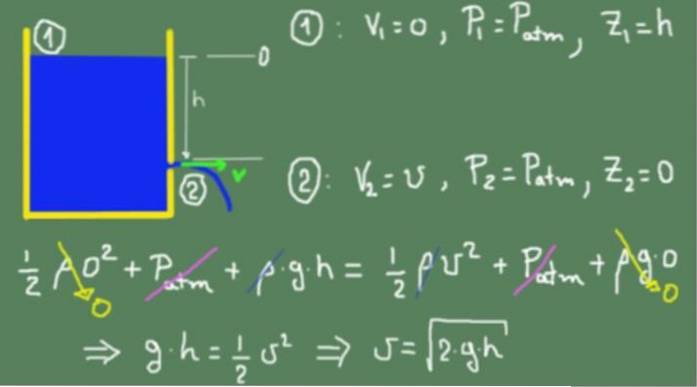
Rutan ovan visar att det erhållna resultatet är detsamma som för ett fritt fallande föremål,
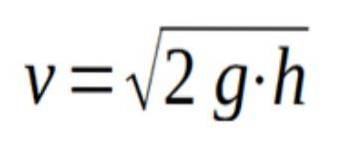
Lösta övningar
Övning 1
Jag) Det lilla utloppsröret till en vattentank är 3 m under vattenytan. Beräkna utloppshastigheten för vattnet.
Lösning:
Följande bild visar hur Torricellis formel tillämpas i detta fall.
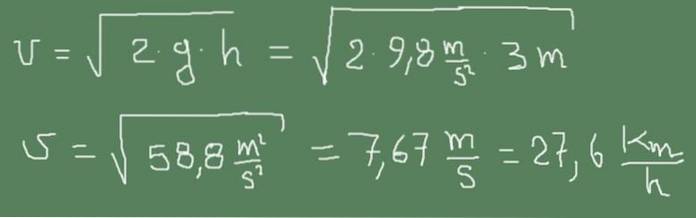
Övning 2
II) Antag att tankens utloppsrör från föregående övning har en diameter på 1 cm, beräkna vattenutloppsflödet.
Lösning:
Flödeshastigheten är den vätskevolym som utgår per tidsenhet och beräknas helt enkelt genom att multiplicera utloppsöppningens yta med utgångshastigheten.
Följande bild visar detaljerna i beräkningen.

Övning 3
III) Bestäm hur hög den fria ytan på vattnet är i en behållare om du vet
att i ett hål i botten av behållaren kommer vattnet ut vid 10 m / s.
Lösning:
Även när hålet är längst ner i behållaren kan Torricelli-formeln fortfarande tillämpas.
Följande bild visar detaljerna i beräkningarna.

Referenser
- Wikipedia. Torricellis sats.
- Hewitt, P. Konceptuell fysik. Femte upplagan.119.
- Young, Hugh. 2016. Sears-Zemanskys universitetsfysik med modern fysik. 14: e upplagan. Pearson. 384.



Ingen har kommenterat den här artikeln än.