
Newtons tredje lagansökningar, experiment och övningar
De Newtons tredje lag, även kallad handlings- och reaktionslag anger att när ett objekt utövar kraft på ett annat utövar det senare på det förstnämnda en kraft av lika storleksordning och riktning och motsatt riktning.
Isaac Newton gjorde sina tre lagar kända 1686 i sin bok Philosophiae Naturalis Principia Mathematica o Matematiska principer för naturfilosofi.

Artikelindex
- 1 Förklaring och formler
- 2 applikationer
- 2.1 Bollmarkinteraktion
- 2.2 Funktion av en raket
- 2.3 Användning av skridskor
- 3 Experiment för barn: åkarna
- 3.1 Formler som används i detta exempel
- 4 Övningen löst
- 4.1 Lösning
- 4.2 Resultat
- 5 exempel på Newtons tredje lag i vardagen
- 5.1 Promenader
- 5.2 Rörelse av bil
- 5.3 Sport
- 5.4 Brandslangar
- 6 Referenser
Förklaring och formler
Den matematiska formuleringen av Newtons tredje lag är mycket enkel:
F12 = -Ftjugoett
En av styrkorna kallas handling och den andra är reaktion. Det är dock nödvändigt att lyfta fram vikten av denna detalj: båda agerar på olika objekt. De gör det också samtidigt, även om denna terminologi felaktigt antyder att åtgärden inträffar före och reaktionen efter..
Eftersom krafter är vektorer betecknas de med fet stil. Denna ekvation indikerar att vi har två objekt: objekt 1 och objekt 2. Kraften F12 är den som utövas av objekt 1 på objekt 2. Kraften Ftjugoett utövas av objekt 2 på objekt 1. Och tecknet (-) indikerar att de är motsatta.
När man noggrant följer Newtons tredje lag observeras en viktig skillnad med de två första: medan de åberopar ett enda objekt hänvisar den tredje lagen till två olika objekt.
Och är det att om du tänker noga kräver interaktioner par objekt.
Av denna anledning upphäver inte handlings- och reaktionskrafterna varandra eller balanserar, trots att de har samma storlek och riktning, utan motsatt riktning: de appliceras på olika kroppar..
Applikationer
Bollmark-interaktion
Här är en mycket daglig användning av en interaktion relaterad till Newtons tredje lag: en vertikalt fallande boll och jorden. Bollen faller till marken eftersom jorden utövar en attraktiv kraft, som kallas gravitation. Denna kraft får bollen att falla med en konstant acceleration på 9,8 m / stvå.
Men knappast någon tänker på det faktum att bollen också utövar en attraktiv kraft på jorden. Naturligtvis förblir jorden oförändrad, eftersom dess massa är mycket större än bollens och därför upplever en försumbar acceleration.
En annan anmärkningsvärd punkt om Newtons tredje lag är att kontakt mellan de två interagerande objekten inte är nödvändig. Det framgår av det just citerade exemplet: bollen har ännu inte kommit i kontakt med jorden, men den utövar ändå sin attraktion. Och bollen på jorden också.
En kraft som tyngdkraften, som verkar otydligt oavsett om det finns kontakt mellan föremål eller inte, kallas en "handlingskraft på avstånd". Å andra sidan kräver krafter som friktion och normal att de samverkande föremålen är i kontakt, det är därför de kallas "kontaktkrafter".
Formler hämtade från exemplet
Återgå till paret objektboll - Jorden, välja index P för bollen och T för jorden och tillämpa Newtons andra lag på varje deltagare i detta system, vi får:
Fresulterande = m.till
Den tredje lagen säger att:
mPtillP = - mTtillT
tillP = 9,8 m / stvå riktas vertikalt nedåt. Eftersom denna rörelse sker längs den vertikala riktningen kan vektornotationen (fetstil) undvikas; och välja uppåtgående riktning så positiv och nedåt som negativ, har vi:
tillP = 9,8 m / stvå
mT ≈ 6 x 10 24 Kg
Oavsett kulans massa är jordens acceleration noll. Det är därför det observeras att bollen faller mot jorden och inte tvärtom..
Drift av en raket
Raketer är ett bra exempel på tillämpning av Newtons tredje lag. Raketten som visas på bilden i början stiger tack vare framdrivningen av heta gaser i hög hastighet.
Många tror att detta händer eftersom dessa gaser på något sätt "lutar" sig mot atmosfären eller på marken för att stödja och driva raketen. Det fungerar inte så.
Precis som raketen utövar kraft på gaserna och driver ut dem bakåt, utövar gaserna en kraft på raketen, som har samma modul men motsatt riktning. Denna kraft är det som ger raketen sin uppåtgående acceleration.
Om du inte har en sådan raket till hands finns det andra sätt att kontrollera att Newtons tredje lag fungerar för att ge framdrivning. Vattenraketer kan byggas, i vilka den nödvändiga kraften tillhandahålls av vattnet som drivs ut med en trycksatt gas..
Det bör noteras att uppstart av en vattenraket tar tid och kräver många försiktighetsåtgärder.
Användning av skridskor
Ett mer överkomligt och omedelbart sätt att kontrollera effekten av Newtons tredje lag är att ta på sig ett par skridskor och driva dig mot en vägg..
För det mesta är förmågan att utöva kraft associerad med föremål som är i rörelse, men sanningen är att orörliga föremål också kan utöva krafter. Åkaren skjuts bakåt tack vare den kraft som den orörliga väggen utövar på honom.
Ytorna i kontakt utövar (normala) kontaktkrafter med varandra. När en bok vilar på ett horisontellt bord utövar den en vertikal kraft som kallas normal på den. Boken utövar på bordet en vertikal kraft med samma numeriska värde och motsatt riktning.
Barnens experiment: åkare
Barn och vuxna kan lätt uppleva Newtons tredje lag och verifiera att handlings- och reaktionskrafterna inte tar bort varandra och kan ge rörelser..
Två åkare på isen eller på en mycket jämn yta kan driva varandra och uppleva rörelser i motsatt riktning, oavsett om de har samma massa eller inte, tack vare lagen om handling och reaktion.
Tänk på två åkare med ganska olika massor. De är mitt i en ishall med försumbar friktion och är initialt i vila. Vid ett givet ögonblick skjuter de varandra genom att applicera konstant kraft med handflatorna. Hur kommer de båda att röra sig?
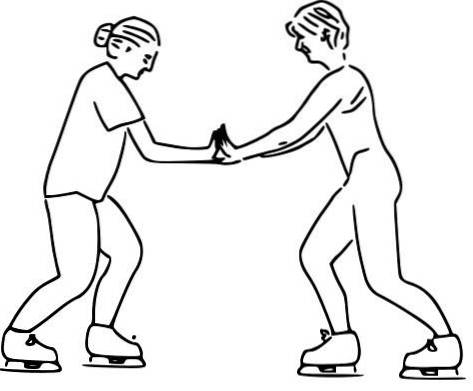
Det är viktigt att notera att eftersom det är en friktionsfri yta, är de enda obalanserade krafterna de krafter som åkarna applicerar på varandra. Även om vikten och den normala verkan på båda, balanserar dessa krafter, annars skulle åkarna accelerera i vertikal riktning.
Formler som används i detta exempel
Newtons tredje lag säger att:
F12 = -Ftjugoett
Det vill säga den kraft som utövas av åkaren 1 mot 2 är lika stor som den som utövas av 2 mot 1, med samma riktning och motsatt riktning. Observera att dessa krafter appliceras på olika objekt, på samma sätt som krafterna applicerades på bollen och jorden i det tidigare konceptexemplet..
m1 till1 = -mtvå tilltvå
Eftersom krafterna är motsatta kommer accelerationerna de orsakar också att vara motsatta, men deras storlek kommer att vara olika, eftersom varje skridskoåkare har olika massa. Låt oss titta på accelerationen som den första åkaren förvärvat:
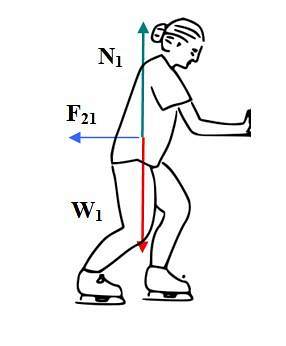
Så rörelsen som händer härnäst är separationen mellan båda åkarna i motsatta riktningar. I princip var åkarna i vila mitt på banan. Var och en utövar en kraft på den andra som ger acceleration så länge händerna är i kontakt och trycket varar.
Därefter rör sig åkarna från varandra med enhetlig rätlinjig rörelse, eftersom obalanserade krafter inte längre verkar. Hastigheten för varje åkare kommer att vara annorlunda om deras massor också är det.
Övningen löst
För att lösa problem där Newtons lagar måste tillämpas är det nödvändigt att noggrant dra de krafter som verkar på objektet. Denna ritning kallas ett "fri kroppsdiagram" eller ett "isolerat kroppsdiagram." Krafterna som kroppen utövar på andra föremål ska inte visas i detta diagram..
Om det är mer än ett föremål inblandat i problemet är det nödvändigt att rita ett frikroppsdiagram för vart och ett av objekten, och kom ihåg att åtgärd-reaktionsparen verkar på olika kroppar..
1- Åkarna i föregående avsnitt har respektive massor m1 = 50 kg och mtvå = 80 kg. De skjuter varandra med en konstant kraft på 200 N. Trycket varar i 0,40 sekunder. Hitta:
a) Acceleration som varje åkare får tack vare dragkraften.
b) Hastigheten för var och en när de separerar
Lösning
a) Ta som den positiva horisontella riktningen den som går från vänster till höger. Genom att tillämpa Newtons andra lag med de värden som anges i uttalandet har vi:

Ftjugoett = m1till1
Varifrån:
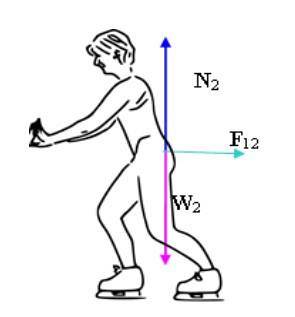
För den andra åkaren:


b) För att beräkna hastigheten som de bär precis när de separeras används de kinematiska ekvationerna med jämnt accelererad rätlinjig rörelse:
Initialhastigheten är 0, eftersom de låg i vila mitt på banan:
vF = vid
vf1 = a1t = -4 m / stvå . 0,40 s = -1,6 m / s
vf2 = atvåt = +2,5 m / stvå . 0,40 s = +1 m / s
Resultat
Som förväntat får person 1, som är lättare, större acceleration och därmed högre hastighet. Notera nu följande om massprodukten och hastigheten för varje åkare:
m1 v1 = 50 kg. (-1,6 m / s) = - 80 kg.m / s
mtvå vtvå = 80 kg. 1 m / s = +80 kg.m / s
Summan av båda produkterna är 0. Produkten av massa och hastighet kallas momentum P. Det är en vektor med samma riktning och hastighetskänsla. När skridskoåkarna var i vila och deras händer var i kontakt kunde man anta att de bildade samma objekt vars fart var:
Peller = (m1 +mtvå) veller = 0
Efter tryckets slut förblir rörelsemängden hos skridskoåkningssystemet 0. Därför bevaras rörelsemängden.
Exempel på Newtons tredje lag i vardagen
Att gå
Walking är en av de mest vardagliga handlingarna som kan utföras. Om det observeras noggrant, krävs det att man går på foten mot marken så att den ger en lika och motsatt kraft på fotgängarens fot..

Det är just den kraften som låter människor gå. Under flygning utövar fåglarna kraft på luften och luften skjuter vingarna så att fågeln driver sig framåt.
Rörelse av en bil
I en bil utövar hjulen kraft på trottoaren. Tack vare trottoarns reaktion utövar den krafter på däcken som driver bilen framåt.
Sport
Inom idrott är handlings- och reaktionskrafterna många och har ett mycket aktivt deltagande.
Låt oss till exempel se idrottaren med sin fot vilande på ett startblock. Blocket ger en normal kraft som reaktion på det tryck som idrottaren utövar på det. Resultatet av detta normala och löparens vikt resulterar i en horisontell kraft som gör att idrottaren kan driva sig framåt..

Brandslangar
Ett annat exempel där Newtons tredje lag finns är brandmän som håller brandslangar. Änden på dessa stora slangar har ett handtag på munstycket som brandmannen måste hålla i när vattenstrålen går ut, för att undvika den rekyl som uppstår när vattnet rusar.
Av samma anledning är det bekvämt att binda båtarna till bryggan innan de lämnar dem, för när man trycker på sig för att nå bryggan, tillhandahålls en kraft till båten som för den bort från den..
Referenser
- Giancoli, D. 2006. Fysik: principer med tillämpningar. Sjätte upplagan. Prentice Hall. 80 - 82.
- Rex, A. 2011. Grundläggande fysik. Pearson. 73 - 75.
- Tipler, P. 2010. Fysik. Volym 1. 5: e upplagan. Redaktionellt Reverté. 94 - 95.
- Stern, D. 2002. Från astronomer till rymdskepp. Hämtad från: pwg.gsfc.nasa.gov.



Ingen har kommenterat den här artikeln än.