
Mekaniskt arbete vad är det, villkor, exempel, övningar
De mekaniskt arbete Det definieras som förändringen i energistillståndet i ett system, orsakad av inverkan av yttre krafter som gravitation eller friktion. Enheterna för mekaniskt arbete i International System (SI) är newton x meter eller joule, förkortat med J.
Matematiskt definieras det som den skalära produkten av kraftvektorn och förskjutningsvektorn. Ja F är den konstanta kraften och l är förskjutningen, båda vektorerna, uttrycks arbetet W som: W = F ● l

När kraften inte är konstant måste vi analysera det arbete som utförts när förskjutningarna är mycket små eller differentiella. I det här fallet, om punkt A betraktas som startpunkt och B som ankomstpunkt, erhålls det totala arbetet genom att lägga till alla bidrag till den. Detta motsvarar beräkning av följande integral:
Variation i systemets energi = Arbete utfört av externa krafter
AE = Wext
När energi adderas till systemet, W> 0 och när energi subtraheras W<0. Ahora bien, si ΔE = 0, puede significar que:
-Systemet är isolerat och det finns inga externa krafter som verkar på det.
-Det finns externa krafter, men de arbetar inte på systemet.
Eftersom förändringen i energi är lika med det arbete som utförs av externa krafter, är SI-enheten också energin. Detta inkluderar alla typer av energi: kinetisk, potential, termisk, kemisk och mer..
Artikelindex
- 1 Villkor för att mekaniskt arbete ska finnas
- 1.1 Tecken på arbete
- 2 Exempel på mekaniskt arbete
- 3 The work-kinetic energy theorem
- 3.1 Arbetet gjort för att sträcka en fjäder
- 4 Övningar
- 4.1 Övning 1
- 4.2 Övning 2
- 5 Referenser
Villkor för mekaniskt arbete
Vi har redan sett att arbete definieras som en punktprodukt. Låt oss ta definitionen av arbete utfört med en konstant kraft och tillämpa konceptet med punktprodukten mellan två vektorer:
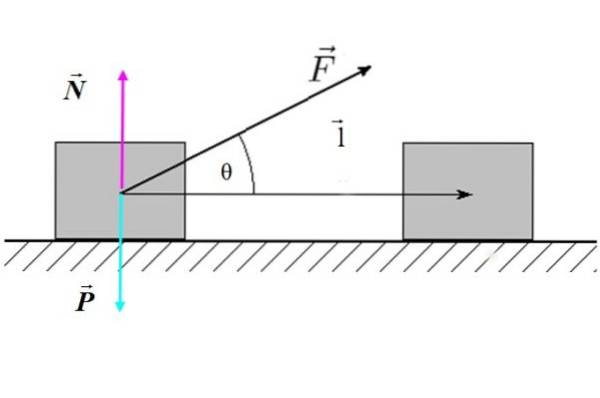
W = F ● l = F.l.cos θ
Var F är kraftens storlek, l är storleken på förskjutningen och θ är vinkeln mellan kraften och förskjutningen. I figur 2 finns ett exempel på en lutande extern kraft som verkar på ett block (systemet), vilket ger en horisontell förskjutning.

Omskriva arbetet enligt följande:
W = (F. cos θ). l
Vi kan konstatera att endast den del av kraften som är parallell med förskjutningen: F. cos θ ekan utföra arbete. Om θ = 90º är cos θ = 0 och arbetet skulle vara noll.
Därför dras slutsatsen att krafterna vinkelrätt mot förskjutningen inte utför mekaniskt arbete.
I fallet med figur 2, varken den normala kraften N inte heller vikten P gör arbete, eftersom båda är vinkelräta mot förskjutningen l.
Tecken på arbete
Som förklarats ovan, W Det kan vara positivt eller negativt. När cos θ> 0, det arbete som utförs av kraften är positivt eftersom det har samma rörelseriktning.
Ja cos θ = 1, kraft och förskjutning är parallella och arbetet är maximalt.
Om cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.
När cos θ = -1, kraft är helt motsatt förskjutning, såsom kinetisk friktion, vars effekt är att sakta ner föremålet på vilket det verkar. Så arbetet är minimalt.
Detta överensstämmer med vad som sägs i början: om arbetet är positivt läggs energi till systemet och om det är negativt subtraherar det.
Nätarbete Wnetto Det definieras som summan av arbetet som utförs av alla krafter som verkar på systemet:
Wnetto = ∑Wi
Då kan vi dra slutsatsen att för att garantera existensen av nätmekaniskt arbete är det nödvändigt att:
-Externa krafter verkar på objektet.
-Dessa krafter är inte alla vinkelräta mot förskjutningen (cos θ ≠ 0).
-De jobb som utförs av varje styrka upphäver inte varandra.
-Det finns en förskjutning.
Exempel på mekaniskt arbete
-Närhelst det krävs för att sätta ett föremål i rörelse från vila är det nödvändigt att utföra mekaniskt arbete. Till exempel skjuta ett kylskåp eller en tung bagageutrymme på en horisontell yta.
-Ett annat exempel på en situation där du behöver göra mekaniskt arbete är att ändra hastigheten på en rörlig boll..
-Arbete krävs för att höja ett föremål till en viss höjd över golvet.
Nu finns det lika vanliga situationer där inte arbete blir gjort, även om framträdanden indikerar något annat. Vi har sagt att för att lyfta ett föremål till en viss höjd måste du göra arbete, så vi bär föremålet, lyfter det över huvudet och håller det där. Gör vi arbete?
Tydligen ja, för om föremålet är tungt kommer armarna att tröttna på kort tid, oavsett hur svårt det är, görs inget arbete ur fysikens synvinkel. Varför inte? Jo för att objektet inte rör sig.
Ett annat fall där det, trots att det har en yttre kraft, inte utför mekaniskt arbete är när partikeln har en jämn cirkelrörelse.
Till exempel ett barn som snurrar en sten bunden till en sträng. Strängspänningen är den centripetala kraften som gör att stenen kan rotera. Men hela tiden är denna kraft vinkelrät mot förskjutningen. Då utför han inte mekaniskt arbete, även om det gynnar rörelse.
The work-kinetic energy theorem
Systemets kinetiska energi är den som det har på grund av dess rörelse. Ja m är massan och v är rörelsens hastighet, den kinetiska energin betecknas med K och ges av:
K = ½ mvtvå
Enligt definition kan ett objekts kinetiska energi inte vara negativ, eftersom både hastigheten och kvadraten av hastigheten alltid är positiva mängder. Den kinetiska energin kan vara 0 när objektet är i vila.
För att ändra systemets kinetiska energi är det nödvändigt att variera dess hastighet - vi kommer att anse att massan förblir konstant, även om detta inte alltid är fallet. Detta kräver att du gör nätarbete på systemet, därför:
Wnetto = ΔK
Detta är arbetet - kinetisk energisats. Den säger att:
Nettoarbete är lika med systemets förändring av kinetisk energi
Observera att även om K alltid är positivt kan ΔK vara positivt eller negativt, eftersom:
AK = Kslutlig - K första
Ja Kslutlig >K första systemet har fått energi och ΔK> 0. Tvärtom, om Kslutlig < K första, systemet har gett upp strömmen.
Arbetet gjort för att sträcka en fjäder
När en fjäder sträcks (eller komprimeras) måste arbetet utföras. Detta arbete lagras på våren, vilket gör att det i sin tur kan arbeta på, till exempel, ett block som är fäst i ena änden..
Hookes lag säger att den kraft som utövas av en fjäder är en återställningskraft - den strider mot förskjutning - och också proportionell mot förskjutningen. Proportionalitetskonstanten beror på hur fjädern är: mjuk och lätt deformerbar eller stel.
Denna kraft ges av:
Fr = -kx
I uttrycket, Fr är kraften, k är vårkonstanten och x är förskjutningen. Det negativa tecknet indikerar att den kraft som utövas av fjädern motsätter sig förskjutningen.
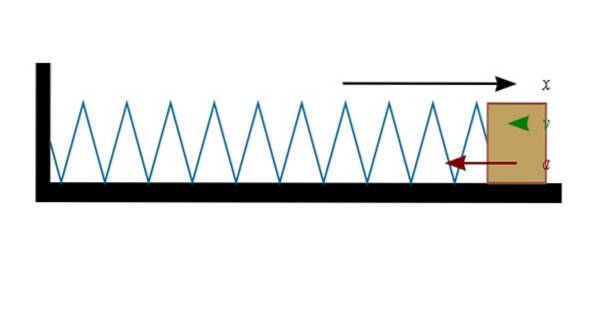
Om fjädern är komprimerad (till vänster i figuren) kommer blocket i slutet att flyttas åt höger. Och när fjädern är sträckt (till höger) vill blocket flytta till vänster.
För att komprimera eller sträcka fjädern måste någon extern agent utföra arbetet, och eftersom det är en variabel kraft, för att beräkna nämnda arbete, måste vi använda definitionen i början:
Det är mycket viktigt att notera att detta är det arbete som utförs av den externa agenten (till exempel en persons hand) för att komprimera eller sträcka fjädern. Det är därför det negativa tecknet inte visas. Och eftersom positionerna är kvadrerade spelar det ingen roll om de är kompressioner eller sträckor..
Arbetet som våren i sin tur kommer att göra på blocket är:
Wvår = -Wext
Träning
Övning 1
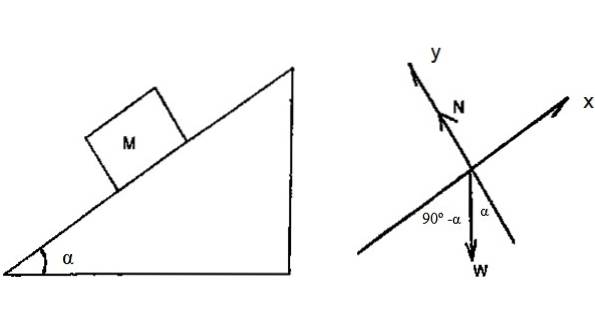
Blocket i figur 4 har massa M = 2 kg och glider nedåt i lutande plan utan friktion, med α = 36,9º. Förutsatt att det är tillåtet att glida från vila från toppen av planet, vars höjd är h = 3 m, hitta den hastighet med vilken blocket når botten av planet, med användning av den kinetiska arbetssatsen.

Lösning
Frikroppsdiagrammet visar att den enda kraften som kan utföra arbete på blocket är vikten. Mer exakt: viktkomponenten längs x-axeln.
Avståndet som blocket har rest på planet beräknas med hjälp av trigonometri:
d = 3 / (cos 36,9º) m = 3,75 m
Wvikt = (Mg). d. cos (90-α) = 2 x 9,8 x 3,75 x cos 53,1 º J = 44,1 J
Genom arbets kinetisk energisats:
Wnetto = ΔK
Wnetto = Wvikt
AK = ½ MvFtvå- ½ Mvellertvå
Eftersom det frigörs från vila, veller = 0, Således:
Wnetto = ½ MvFtvå

Övning 2
En horisontell fjäder, vars konstant är k = 750 N / m, är fäst i ena änden till en vägg. En person komprimerar den andra änden ett avstånd på 5 cm. Beräkna: a) Kraften som utövas av personen, b) Arbetet han gjorde för att komprimera fjädern.
Lösning
a) Storleken på den kraft som personen applicerar är:
F = kx = 750 N / m. 5x10 -två m = 37,5 N.
b) Om fjäderns ände ursprungligen är på x1 = 0, för att ta det därifrån till slutposition xtvå = 5 cm, är det nödvändigt att göra följande arbete, enligt resultatet som erhållits i föregående avsnitt:
Wext = ½ k (xtvåtvå - x1två) = 0,5 x 750 x (0,05två -0tvåJ = 0,9375 J.
Referenser
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 2. Dynamik. Redigerad av Douglas Figueroa (USB).
- Iparraguirre, L. 2009. Grundläggande mekanik. Samling för naturvetenskap och matematik. Gratis online distribution.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Fysik Libretexts. Sats på arbetsenergi. Återställd från: phys.libretexts.org
- Arbete och energi. Återställd från: physics.bu.edu
- Arbete, energi och kraft. Hämtad från: ncert.nic.in



Ingen har kommenterat den här artikeln än.