
Isometrisk transformationskomposition, typer och exempel

De isometriska transformationer De är förändringar i en viss figurs position eller orientering som inte ändrar dess form eller storlek. Dessa omvandlingar klassificeras i tre typer: translation, rotation och reflektion (isometri). Generellt låter geometriska transformationer dig skapa en ny figur från en given.
En omvandling till en geometrisk figur innebär att den på något sätt har genomgått en viss förändring; det vill säga det ändrades. Enligt känslan av originalet och liknande i planet kan geometriska transformationer klassificeras i tre typer: isometrisk, isomorf och anamorf..

Artikelindex
- 1 Funktioner
- 2 typer
- 2.1 Genom översättning
- 2.2 Genom rotation
- 2.3 Genom reflektion eller symmetri
- 3 Sammansättning
- 3.1 Sammansättning av en översättning
- 3.2 Sammansättning av en rotation
- 3.3 Sammansättning av en symmetri
- 4 Referenser
Egenskaper
Isometriska omvandlingar inträffar när storleken på segmenten och vinklarna mellan originalfiguren och den transformerade figuren bevaras.
I denna typ av transformation förändras varken formen eller storleken på figuren (de är kongruenta), det är bara en förändring i dess position, antingen i orientering eller i riktning. På detta sätt kommer de initiala och slutliga siffrorna att vara lika och geometriskt kongruenta..
Isometri avser jämlikhet; det vill säga geometriska figurer är isometriska om de har samma form och storlek.
Vid isometriska transformationer är det enda som kan observeras en förändring av positionen i planet, en styv rörelse uppstår tack vare vilken figuren går från en initial position till en slutlig. Denna siffra kallas homolog (liknande) av originalet.
Det finns tre typer av rörelser som klassificerar en isometrisk transformation: översättning, rotation och reflektion eller symmetri.
Typer
Genom översättning
De är de isometrier som gör att alla punkter i planet kan förskjutas i en rak linje i en given riktning och ett visst avstånd.
När en figur transformeras genom översättning ändrar den inte sin orientering i förhållande till utgångsläget, och förlorar inte heller sina inre mått, måtten på dess vinklar och sidor. Denna typ av förskjutning definieras av tre parametrar:
- En riktning, som kan vara horisontell, vertikal eller sned.
- En känsla, som kan vara vänster, höger, upp eller ner.
- Avstånd eller storlek, vilket är längden från utgångsläget till slutet av varje punkt som rör sig.
För att en isometrisk transformation genom översättning ska kunna uppfyllas måste följande villkor vara uppfyllda:
- Figuren måste alltid hålla alla dess dimensioner, både linjära och vinklade.
- Figuren ändrar inte sin position i förhållande till den horisontella axeln; det vill säga dess vinkel varierar aldrig.
- Översättningarna kommer alltid att sammanfattas i en enda, oavsett antalet översättningar som görs..
I ett plan där centrum är en punkt O, med koordinater (0,0), definieras översättningen av en vektor T (a, b), som indikerar förskjutningen av den initiala punkten. Nämligen:
P (x, y) + T (a, b) = P '(x + a, y + b)
Till exempel, om en översättning T (-4, 7) tillämpas på koordinatpunkten P (8, -2), får vi:
P (8, -2) + T (-4, 7) = P '[(8 + (-4)), ((-2) + 7)] = P' (4, 5)
I följande bild (till vänster) kan man se hur punkt C rörde sig för att sammanfalla med D. Det gjorde det i vertikal riktning, riktningen var uppåt och CD-avståndet eller storleken var 8 meter. I den högra bilden observeras översättningen av en triangel:
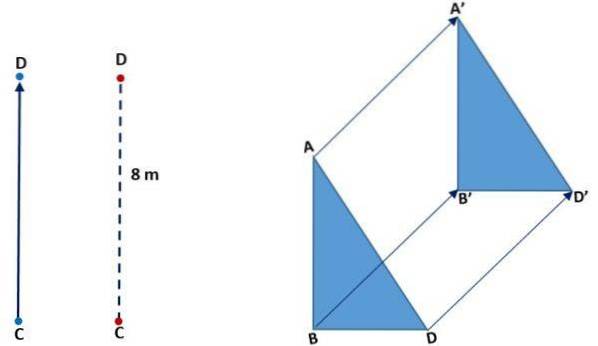
Genom rotation
De är de isometrier som gör att figuren kan rotera alla punkter i ett plan. Varje punkt roterar efter en båge som har en konstant vinkel och en fast punkt (rotationscentrum) bestämd.
Det vill säga all rotation kommer att definieras av dess rotationscentrum och rotationsvinkel. När en figur transformeras genom rotation behåller den måttet på dess vinklar och sidor.
Rotationen sker i en viss riktning, den är positiv när rotationen är moturs (moturs) och negativ när den är medurs..
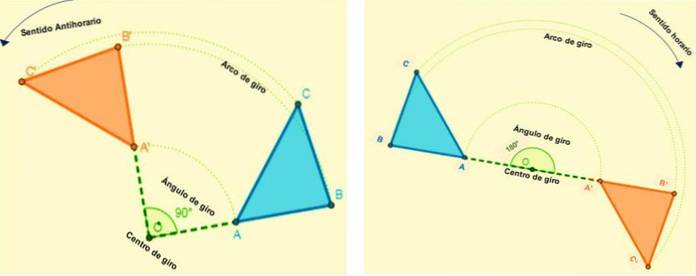
Om en punkt (x, y) roteras med avseende på ursprunget - det vill säga dess rotationscentrum är (0,0) -, med en vinkel på 90eller till 360eller koordinaterna för punkterna kommer att vara:
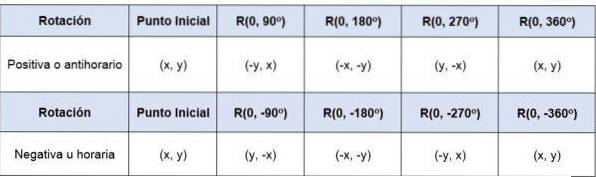
I det fall rotationen inte har ett centrum vid ursprunget måste koordinatsystemets ursprung överföras till det nya angivna ursprunget för att kunna rotera figuren med ursprunget som centrum..
Till exempel om punkten P (-5,2) roteras 90eller, runt ursprunget och i en positiv riktning kommer dess nya koordinater att vara (-2,5).
Genom reflektion eller symmetri
De är de transformationer som inverterar planens punkter och figurer. Denna inversion kan vara med avseende på en punkt eller det kan också vara med avseende på en linje.
Med andra ord, i denna typ av transformation är varje punkt i den ursprungliga figuren associerad med en annan punkt (bild) på den homologa figuren, på ett sådant sätt att punkten och dess bild ligger på samma avstånd från en linje som kallas axeln av symmetri..
Således kommer den vänstra delen av figuren att vara en reflektion av den högra delen utan att ändra dess form eller dimensioner. Symmetri förvandlar en figur till en annan lika men i motsatt riktning, vilket framgår av följande bild:
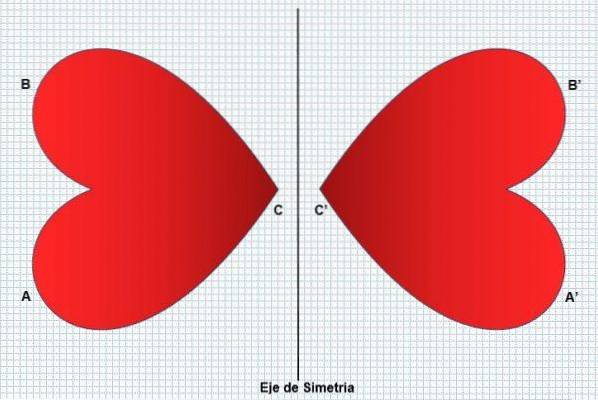
Symmetri finns i många aspekter, till exempel i vissa växter (solrosor), djur (påfågel) och naturfenomen (snöflingor). Människan reflekterar det i ansiktet, vilket anses vara en skönhetsfaktor. Reflektion eller symmetri kan vara av två typer:
Central symmetri
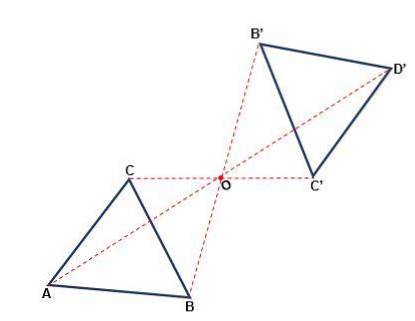
Det är den transformation som sker med avseende på en punkt där figuren kan ändra sin orientering. Varje punkt i den ursprungliga figuren och dess bild ligger på samma avstånd från en punkt O, kallad centrum för symmetri. Symmetri är central när:
- Både punkten och dess bild och mitt hör till samma linje.
- Med en rotation på 180eller från centrum O erhålls en siffra som är lika med originalet.
- Stroken i den ursprungliga figuren är parallell med den bildade figurens slag.
- Bildens känsla förändras inte, den kommer alltid att vara medurs.
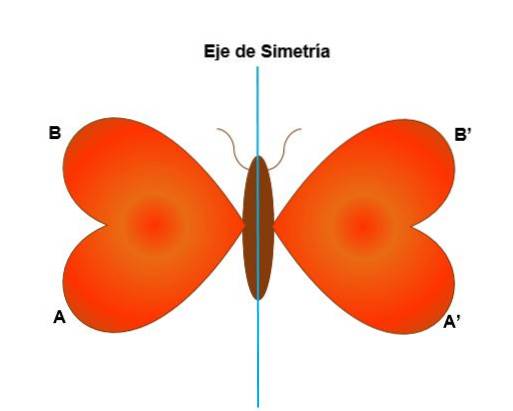
Denna omvandling sker med avseende på symmetriaxeln, där varje punkt i den ursprungliga figuren är associerad med en annan punkt i bilden och dessa ligger på samma avstånd från symmetriaxeln. Symmetri är axiell när:
- Segmentet som förenar en punkt med sin bild är vinkelrät mot dess symmetriaxel.
- Siffrorna ändrar riktning med avseende på rotation eller medurs riktning.
- När figuren delas med en central linje (symmetriaxel) sammanfaller en av de resulterande halvorna helt med en annan av halvorna.
Sammansättning
En sammansättning av isometriska transformationer hänvisar till den successiva tillämpningen av isometriska transformationer på samma figur.
Sammansättning av en översättning
Sammansättningen av två översättningar resulterar i en annan översättning. När den utförs på planet ändras endast den axelns koordinater på den horisontella axeln (x), medan koordinaterna för den vertikala axeln (y) förblir desamma, och vice versa.
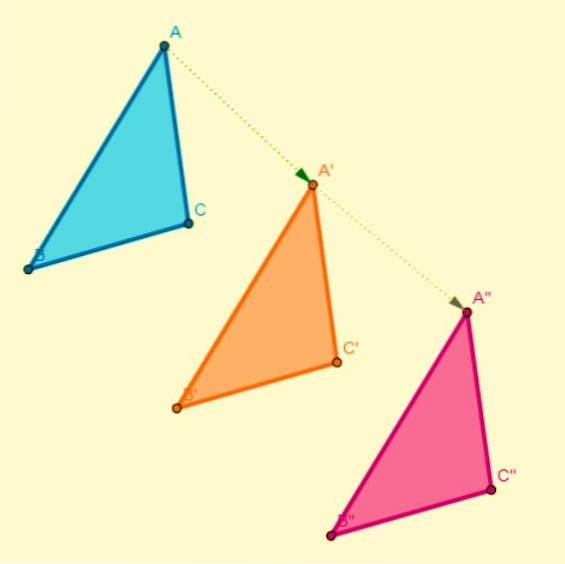
Sammansättning av en rotation
Sammansättningen av två varv med samma centrum resulterar i en annan varv, som har samma centrum och vars amplitud kommer att vara summan av amplituden för de två varven..
Om svängarnas mittpunkt har en annan mittpunkt kommer skärningen av halveringen av två segment av liknande punkter att vara centrum för svängen.
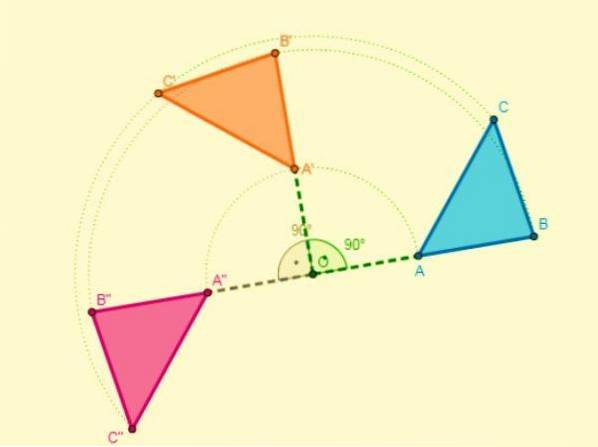
Sammansättning av en symmetri
I detta fall beror kompositionen på hur den appliceras:
- Om samma symmetri tillämpas två gånger blir resultatet en identitet.
- Om två symmetrier tillämpas med avseende på två parallella axlar blir resultatet en översättning och dess förskjutning är dubbelt så långt som dessa axlar:
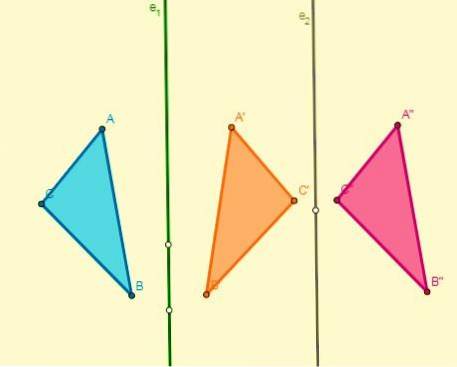
- Om två symmetrier appliceras med avseende på två axlar som skär varandra vid punkt O (centrum), kommer en rotation med centrum vid O att erhållas och dess vinkel blir dubbelt så stor som vinkeln som bildas av axlarna:
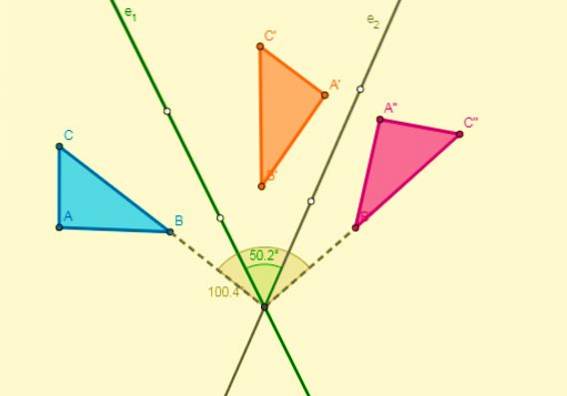
Referenser
- V Burgués, J. F. (1988). Material för konstruktion av geometri. Madrid: syntes.
- Cesar Calavera, I. J. (2013). Teknisk ritning II. Paraninfo S.A: Editions of the Tower.
- Coxeter, H. (1971). Grunderna för geometri. Mexiko: Limusa-Wiley.
- Coxford, A. (1971). Geometri En transformationsstrategi. USA: Laidlaw Brothers.
- Liliana Siñeriz, R. S. (2005). Induktion och formalisering i undervisningen av styva transformationer i CABRI-miljön.
- , P. J. (1996). Gruppen av isometrier på planet. Madrid: syntes.
- Suárez, A. C. (2010). Transformationer i planet. Gurabo, Puerto Rico: AMCT .



Ingen har kommenterat den här artikeln än.