
Isosceles trapezegenskaper, förhållanden och formler, exempel
A trapets likbent är en fyrkant där två av sidorna är parallella med varandra och dessutom har de två vinklarna intill en av dessa parallella sidor samma mått.
I figur 1 har vi fyrsidiga ABCD, där sidorna AD och BC är parallella. Dessutom har vinklarna ∠DAB och ∠ADC intill den parallella sidan AD samma mått α.
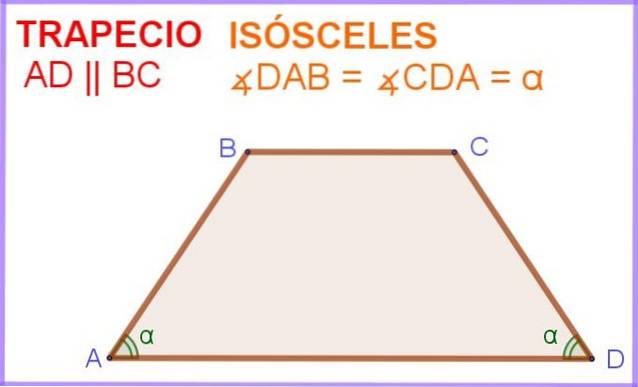
Så denna fyrsidiga eller fyrsidiga polygon är i själva verket en likbent trapes.
I en trapets kallas de parallella sidorna baser och de icke-parallellerna kallas lateral. En annan viktig funktion är höjd, vilket är avståndet som skiljer de parallella sidorna.
Förutom likbent trapezoid finns det andra typer av trapezoid:
-Tskalen marulk, som har alla sina olika vinklar och sidor.
-Trektangel havsfisk, i vilken en lateral har rätt intilliggande vinklar.
Den trapezformiga formen är vanlig inom olika områden inom design, arkitektur, elektronik, beräkning och många fler, vilket kommer att ses senare. Därav vikten av att bli bekant med dess egenskaper.
Artikelindex
- 1 Fastigheter
- 1.1 Uteslutande av likbent trapes
- 1.2 För alla trapezider
- 2 Relationer och formler
- 2.1 Unika förhållanden mellan isosceles trapezium
- 2.2 Relationer för varje trapets
- 2.3 Förhållanden för likbent trapes med inskriven omkrets
- 2.4 Formler för att bestämma ena sidan, känna till de andra och en vinkel
- 2.5 Bestämning av ena sidan, att känna till de andra och en diagonal
- 2.6 Bas från höjd, yta och annan bas
- 2.7 Kända sidobaser, yta och vinkel
- 2.8 Känd lateral median, area och vinkel
- 2.9 Känd sidohöjd
- 2.10 Känd höjd i vinkel och två sidor
- 2.11 Kända diagonaler alla sidor, eller två sidor och en vinkel
- 2.12 Omkretsen av den likbeniga triangeln
- 2.13 Arean av likbent trapes
- 2.14 Omkretsens radie
- 3 Exempel på användning av likbent trapes
- 3.1 Inom arkitektur och konstruktion
- 3.2 I design
- 4 Lösta övningar
- 4.1 - Övning 1
- 4.2 - Övning 2
- 5 Referenser
Egenskaper
Exklusivt för likbent trapes
Om en trapets är likbenad har den följande karakteristiska egenskaper:
1.- Sidorna har samma mått.
2. - Vinklarna intill baserna är lika.
3.- Motsatta vinklar är kompletterande.
4. - Diagonalerna har samma längd, de två segmenten som förbinder motsatta hörn är lika.
5.- Vinkeln som bildas mellan baserna och diagonalerna har samma mått.
6.- Den har en begränsad omkrets.
Omvänt, om en trapezoid uppfyller någon av ovanstående egenskaper, är det en likbent trapezoid.
Om i en likbent trapezoid är en av vinklarna rätt (90º), så kommer alla andra vinklar att vara rätt och bildar en rektangel. Det vill säga en rektangel är ett särskilt fall av likbent trapes.

För all trapets
Följande uppsättning egenskaper är giltiga för alla trapesform:
7.- The median av trapezium, det vill säga det segment som förenar mittpunkterna på dess icke-parallella sidor, är parallellt med någon av baserna.
8.- Medianns längd är lika med semisumman (summan dividerad med 2) av dess baser.
9.- En trapetsformats median skär sina diagonaler vid mittpunkten.
10. - Diagonalerna på en trapets skär varandra vid en punkt som delar dem i två sektioner som är proportionella mot basernas kvoter..
11.- Summan av kvadraterna av diagonalerna för en trapets är lika med summan av kvadraten på dess sidor plus den dubbla produkten av dess baser.
12.- Det segment som förenar diagonalernas mittpunkter har en längd som är lika med basens semidifferens.
13. - Vinklarna intill de laterala är kompletterande.
14. - En trapes har en inskriven omkrets om och bara om summan av dess baser är lika med summan av dess sidor.
15.- Om en trapets har en inskriven omkrets, är vinklarna med ett toppunkt i mitten av omkretsen och sidor som passerar genom ändarna på samma sida rätt vinklar.
Relationer och formler
Följande uppsättning förhållanden och formler hänvisar till figur 3, där förutom likbent trapezoid visas andra viktiga segment som redan nämnts, såsom diagonaler, höjd och median.
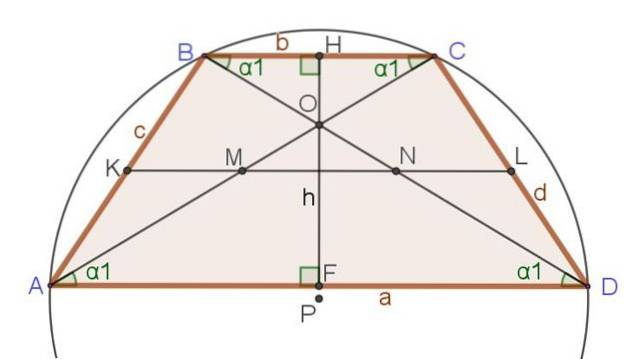
Unika förhållanden mellan den likbeniga trapesen
1.- AB = DC = c = d
2.- ∡DAB = ∡CDA och ∡ABC = ∡BCD
3.- ∡DAB + ∡BCD = 180º och ∡CDA + ∡ABC = 180º
4.- BD = AC
5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α1
6.- A, B, C och D tillhör den begränsade cirkeln.
Förhållanden för alla trapes
- Om AK = KB och DL = LC ⇒ KL || AD och KL || före Kristus
8.- KL = (AD + BC) / 2
9.- AM = MC = AC / 2 och DN = NB = DB / 2
10.- AO / OC = AD / BC och DO / OB = AD / BC
11.- ACtvå + DBtvå = ABtvå + DCtvå + 2⋅AD⋅BC
12.- MN = (AD - BC) / 2
13.- ∡DAB + ∡ABC = 180º och ∡CDA + ∡BCD = 180º
14.- Om AD + BC = AB + DC ⇒ ∃ R än lika långt från AD, BC, AB och DC
15.- Om ∃ R är lika långt från AD, BC, AB och DC, då:
∡BRA = ∡DRC = 90º
Förhållanden för likbent trapes med inskriven omkrets
Om summan av baserna i en likbent trapezoid är lika med två gånger en lateral, så finns den inskrivna omkretsen.

Följande egenskaper gäller när likbent trapes har en inskriven omkrets (se figur 4 ovan):
16.- KL = AB = DC = (AD + BC) / 2
17. - Diagonalerna skär varandra i rät vinkel: AC ⊥ BD
18.- Höjden mäter samma som medianen: HF = KL, det vill säga h = m.
19.- Kvadraten på höjden är lika med basens produkt: htvå = BC⋅AD
20.- Under dessa specifika förhållanden är trapetsens yta lika med kvadraten på höjden eller basprodukten: Area = htvå = BC⋅AD.
Formler för att bestämma ena sidan, känna till de andra och en vinkel
Känd en bas, den laterala och en vinkel, den andra basen kan bestämmas av:
a = b + 2c Cos a
b = a - 2c Cos a
Om längden på baserna och en vinkel anges som kända data är längderna på båda sidor:
c = (a - b) / (2 Cos a)
Bestämning av ena sidan, att känna till de andra och en diagonal
a = (d1två - ctvå) / b;
b = (d1två - ctvå) / till
c = √ (d1två - a⋅b)
Var d1 är längden på diagonalerna.
Bas från höjd, yta och annan bas
a = (2 A) / h - b
b = (2 A) / h - a
Kända sidobaser, yta och vinkel
c = (2A) / [(a + b) sin a]
Känd lateral median, area och vinkel
c = A / (m sin a)
Känd höjd på sidorna
h = √ [4 ctvå - (a - b)två]
Känd höjd i vinkel och två sidor
h = tg α⋅ (a - b) / 2 = c. sin α
Kända diagonaler alla sidor, eller två sidor och en vinkel
d1 = √ (ctvå+ a b)
d1 = √ (atvå+ ctvå - 2 a c Cos α)
d1 = √ (btvå + ctvå- 2 b c Cos β)
Omkretsen av den likbeniga triangeln
P = a + b + 2c
Isosceles trapezium
Det finns flera formler för att beräkna området, beroende på vilken data som är känd. Följande är det mest kända, beroende på bas och höjd:
A = h⋅ (a + b) / 2
Och du kan också använda dessa andra:
-Om sidorna är kända
A = [(a + b) / 4] √ [4ctvå - (a - b)två]
-När du har två sidor och en vinkel
A = (b + c Cos α) c Sen α = (a - c Cos α) c Sen α
-Om den inskrivna cirkelns radie och en vinkel är kända
A = 4 rtvå / Sen a = 4 rtvå / Sen β
-När baserna och en vinkel är kända
A = a⋅b / Sen α = a⋅b / Sen β
-Om trapesformen kan skrivas in en omkrets
A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2
-Kända diagonalerna och vinkeln de bildar med varandra
A = (d1två/ 2) Sen y = (d1två / 2) Sen 5
-När du har lateral, median och en vinkel
A = mc.sen α = mc.sen β
Radien på den begränsade cirkeln
Endast likbent trapezoider har en begränsad omkrets. Om den större basen a är lateral c och diagonal d kända1, då är radien R för cirkeln som passerar genom trapetsformens fyra hörn:
R = a⋅c⋅d1 / 4√ [p (p -a) (p -c) (p-d1)]
Där p = (a + c + d1) / två
Exempel på användning av likbent trapes
Den likbeniga trapesen uppträder inom designfältet, vilket framgår av figur 2. Och här är några ytterligare exempel:
Inom arkitektur och konstruktion
De forntida inkaerna kände till den likbeniga trapesen och använde den som byggnadselement i detta fönster i Cuzco, Peru:

Och här visas trapesen igen i samtalet trapesformigt ark, ett material som ofta används i konstruktionen:

I design
Vi har redan sett att den likbeniga trapezoid förekommer i vardagliga föremål, inklusive mat som denna chokladkaka:

Lösta övningar
- Övning 1
En likbent trapez har en bas större än 9 cm, en bas mindre än 3 cm och dess diagonaler 8 cm vardera. Beräkna:
a) Sida
b) Höjd
c) Omkrets
d) Område
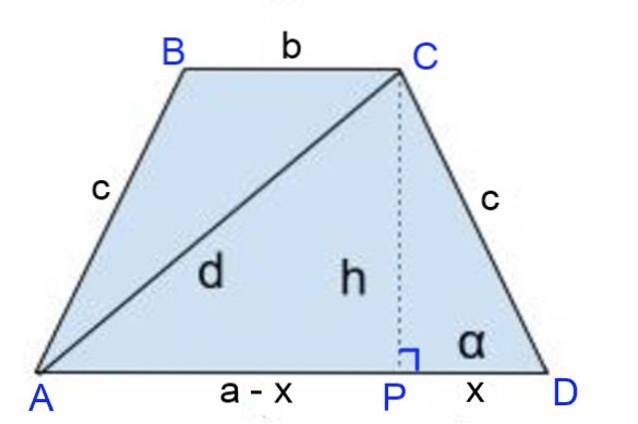
Lösning till
Höjden CP = h ritas in, där höjdens fot definierar segmenten:
PD = x = (a-b) / 2 y
AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.
Använda Pythagoras sats till höger triangel DPC:
ctvå = htvå + (a - b)två / 4
Och även till höger triangel APC:
dtvå = htvå + APtvå = htvå + (a + b)två / 4
Slutligen, medlem för medlem, subtraheras den andra ekvationen från den första och förenklas:
dtvå - ctvå = ¼ [(a + b)två - (a-b)två] = ¼ [(a + b + a-b) (a + b-a + b)]
dtvå - ctvå = ¼ [2a 2b] = a b
ctvå= dtvå - a b ⇒ c = √ (dtvå - a b) = √ (8två - 9⋅3) = √37 = 6,08 cm
Lösning b
htvå = dtvå - (a + b)två / 4 = 8två - (12två / tvåtvå ) = 8två - 6två = 28
h = 2 √7 = 5,29 cm
Lösning c
Perimeter = a + b + 2 c = 9 + 3 + 2⋅6,083 = 24,166 cm
Lösning d
Area = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm
- Övning 2
Det finns en likbent trapezoid vars största bas är två gånger den minsta och dess minsta bas är lika med höjden, som är 6 cm. Besluta:
a) Sidans längd
b) Omkrets
c) Område
d) Vinklar
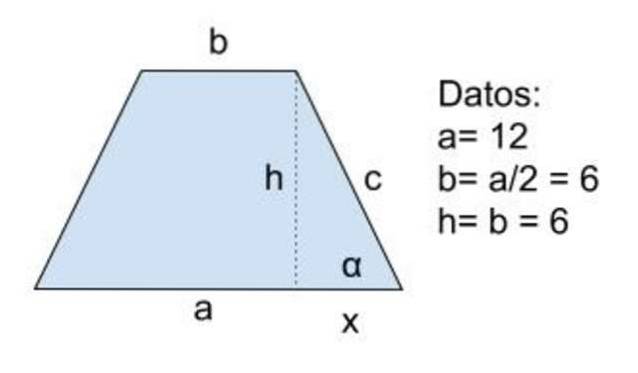
Lösning till
Data: a = 12, b = a / 2 = 6 och h = b = 6
Vi fortsätter på detta sätt: höjden h ritas och den pythagoreiska satsen appliceras på hypotenus triangeln "c" och benen h och x:
ctvå = htvå+xctvå
Då måste du beräkna värdet på höjden från data (h = b) och det för benet x:
a = b + 2 x ⇒ x = (a-b) / 2
Att ersätta de tidigare uttrycken vi har:
ctvå = btvå+(a-b)två/tvåtvå
Nu introduceras de numeriska värdena och det förenklas:
ctvå = 62+ (12-6) 2/4
ctvå = 62 (1 + ¼) = 62 (5/4)
Erhållande:
c = 3√5 = 6,71 cm
Lösning b
Omkretsen P = a + b + 2 c
P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm
Lösning c
Området som funktion av basens höjd och längd är:
A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 cmtvå
Lösning d
Vinkeln a bildad av lateral med större bas erhålls genom trigonometri:
Tan (α) = h / x = 6/3 = 2
α = ArcTan (2) = 63,44º
Den andra vinkeln, den som bildar lateral med den mindre basen, är β, som är kompletterande till α:
β = 180º - α = 180º - 63.44º = 116.56º
Referenser
- E. A. 2003. Element av geometri: med övningar och kompassgeometri. University of Medellin.
- Campos, F. 2014. Matematik 2. Grupo Editorial Patria.
- Freed, K. 2007. Upptäck polygoner. Benchmark Education Company.
- Hendrik, V. 2013. Allmänna polygoner. Birkhäuser.
- IGER. Matematik första terminen Tacaná. IGER.
- Jr. geometri. 2014. Polygoner. Lulu Press, Inc..
- Miller, Heeren och Hornsby. 2006. Matematik: resonemang och tillämpningar. 10: e. Utgåva. Pearson Education.
- Patiño, M. 2006. Matematik 5. Redaktionellt program.
- Wikipedia. Trapets. Återställd från: es.wikipedia.com


Ingen har kommenterat den här artikeln än.