De bana i fysik Det är kurvan som en mobil beskriver när den passerar på varandra följande punkter under sin rörelse. Eftersom det kan anta ett oändligt antal varianter, så kommer banorna som mobilen kan följa.
För att komma från ett ställe till ett annat kan en person ta olika vägar och olika sätt: till fots genom trottoarerna på gator och alléer, eller anländer med bil eller motorcykel på en motorväg. Under en promenad genom skogen kan vandraren följa en komplicerad stig som inkluderar svängar, går upp eller ner i nivå och till och med passerar genom samma punkt flera gånger.
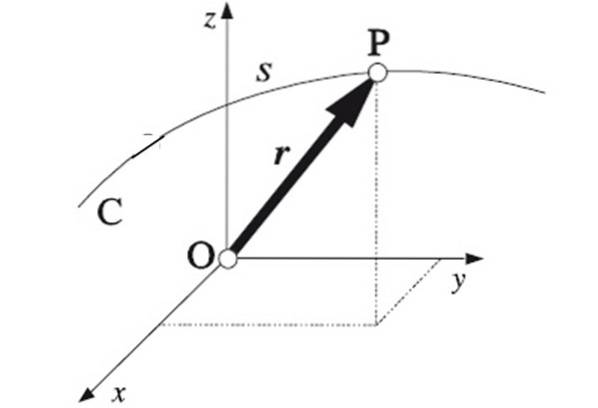
Om de punkter genom vilka mobilen färdas följer en rak linje kommer banan att vara rätlinjig. Detta är den enklaste vägen, eftersom den är endimensionell. För att ange position krävs en enda koordinat.
Men mobilen kan följa en krökt väg och kunna stängas eller vara öppen. I dessa fall kräver spårning av positionen två eller tre koordinater. Dessa är rörelser i planet respektive i rymden. Detta har att göra med länkar: materiella förhållanden som begränsar rörelsen. Några exempel är:
- Banorna som beskriver planeterna runt solen är slutna ellipsformade stigar. Även om de i vissa fall kan approximeras till en cirkulär, som i fallet med jorden.
- Bollen som målvakten sparkar i en målspark följer en parabolisk bana.
- En fågel i flygning beskriver krökta banor i rymden, förutom att röra sig på ett plan kan den gå upp eller ner i nivå efter behag.
Banan i fysik kan uttryckas matematiskt när mobilens position är känd när som helst. Vara r positionsvektorn, som i sin tur har koordinater x, Y Y z i det mest allmänna fallet med en rörelse i tre dimensioner. Att känna till funktionen r (t) banan kommer att bestämmas helt.
Artikelindex
Generellt sett kan banan vara en ganska komplicerad kurva, särskilt om du vill uttrycka den matematiskt. Av den anledningen börjar det med de enklaste modellerna, där mobilerna färdas i en rak linje eller på ett plan, vilket kan vara golvet eller någon annan lämplig:
De mest studerade banorna är:
- Rätlinjig, när du reser på en rak horisontell, vertikal eller lutande linje. En boll som kastas vertikalt uppåt följer denna bana, eller ett föremål som glider nerför en lutning följer. De är endimensionella rörelser, en enda koordinat räcker för att helt bestämma deras position..
- Parabolisk, där mobilen beskriver en båge av en parabel. Det är frekvent, eftersom varje objekt som kastas snett under tyngdkraftsverkan (en projektil) följer denna bana. För att ange mobilens position måste du ange två koordinater: x Y Y.
- Cirkulär, uppstår när den rörliga partikeln följer en cirkel. Det är också vanligt i naturen och i daglig praxis. Många vardagliga föremål följer en cirkulär väg som däck, maskindelar och satelliter som kretsar, för att nämna några..
- Elliptisk, objektet rör sig efter en ellips. Som sagt i början är det vägen som följs av planeterna i omloppsbana runt solen.
- Hyperbolisk, Astronomiska föremål under påverkan av en central kraft (gravitation) kan följa elliptiska (stängda) eller hyperboliska (öppna) banor, dessa är mindre frekventa än de tidigare.
- Helical, eller spiralrörelse, som för en fågel som stiger upp i en termisk ström.
- Gunga eller pendel, mobilen beskriver en båge i fram och tillbaka rörelser.
Banorna som beskrivs i föregående avsnitt är mycket användbara för att snabbt få en uppfattning om hur ett objekt rör sig. I vilket fall som helst är det nödvändigt att klargöra att banan för en mobil beror på observatörens plats. Detta innebär att samma händelse kan ses på olika sätt, beroende på var varje person är..
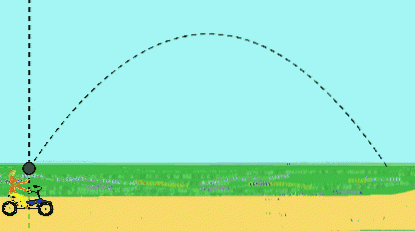
Till exempel trampar en tjej i konstant hastighet och kastar en boll uppåt. Hon observerar att bollen beskriver en raklinjig väg.
Men för en observatör som står på vägen som ser den passera kommer bollen att ha en parabolisk rörelse. För honom kastades bollen inledningsvis med en lutande hastighet, ett resultat av hastigheten uppåt av flickans hand plus cykelns hastighet..
- Explicit, direkt ange kurvan eller stället som ges av ekvationen y (x)
- Implicit, där en kurva uttrycks som f (x, y, z) = 0
-Parametrisk, i denna form ges x-, y- och z-koordinaterna som en funktion av en parameter som vanligtvis väljs som tid t. I detta fall består banan av funktionerna: x (t), och t) Y z (t).
Därefter beskrivs två banor som har studerats allmänt inom kinematik: den paraboliska banan och den cirkulära banan..
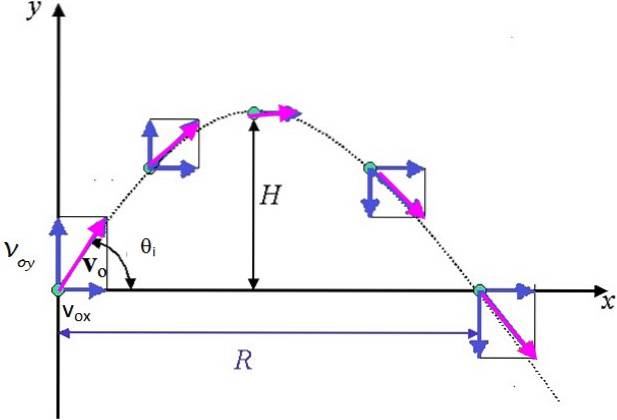
Ett objekt (projektilen) kastas i en vinkel a med den horisontella och med initial hastighet veller som bilden visar. Luftmotstånd tas inte med i beräkningen. Rörelsen kan behandlas som två oberoende och samtidiga rörelser: en horisontell med konstant hastighet och den andra vertikal under tyngdkraftsverkan..
x (t) = xeller +voxe.t
y (t) = yeller +vHallå.t -½g.ttvå
Dessa ekvationer är parametriska ekvationer projektiluppskjutning. Som förklarats ovan har de parametern t, vad är tid.
Följande kan ses i höger triangel i figuren:
voxe = veller cos θi
vHallå = veller sen θi
Att ersätta dessa ekvationer som innehåller startvinkeln i de parametriska ekvationerna:
x (t) = xeller +veller cos θi.t
y (t) = yeller +veller. sen θi.t -½g.ttvå
Banans explicita ekvation hittas genom att lösa t från ekvationen för x (t) och ersätta y (t) i ekvationen. För att underlätta algebraiskt arbete kan man anta att ursprunget (0,0) ligger vid startpunkten och därmed xeller = ocheller = 0.
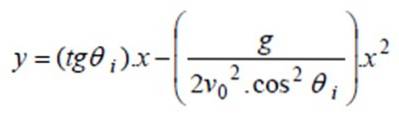
Detta är ekvationen för vägen in tydligt sätt.
En cirkulär väg ges av:
(x - xeller)två + (och ocheller)två = Rtvå
Här xeller och ocheller representerar centrum av cirkeln som beskrivs av mobilen och R är dess radie. P (x, y) är en punkt på vägen. Från den skuggade högra triangeln (figur 3) kan man se att:
x = R. cos θ
y = R. sin θ
Parametern är i detta fall svepvinkeln called, kallad vinkelförskjutning. I det speciella fallet att vinkelhastigheten ω (vinkel svept per tidsenhet) är konstant, kan man säga att:
θ = θeller + ωt
Var θeller är partikelns ursprungliga vinkelläge, som om det tas som 0, minskar till:
θ = ωt
I ett sådant fall återgår tiden till parametriska ekvationer som:
x = R.cos ωt
y = R. sin ωt
Enhetsvektorerna i Y j är mycket praktiska för att skriva ett objekts positionsfunktion r (t). De anger riktningarna på axeln x och på axeln Y respektive. I sina termer är positionen för en partikel som beskriver en enhetlig cirkulär rörelse:
r (t) = R.cos ωt i + R. sen ωt j
En kanon kan skjuta en kula med en hastighet på 200 m / s och en vinkel på 40 ° i förhållande till horisontalplanet. Om kastet är på plan mark och luftmotståndet försummas, hitta:
a) Banans ekvation y (x) ...
b) Parametriska ekvationer x (t) Y och t).
c) Det horisontella intervallet och tiden som projektilen varar i luften.
d) Höjden på vilken projektilen är när x = 12 000 m
a) För att hitta banan ersätts värdena i ekvationen y (x) i föregående avsnitt:
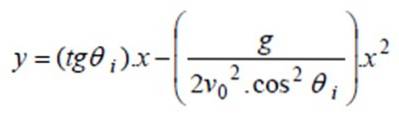
y (x) = tg 40º. x - 9.8 / (2 '400två. costvå40: e) xtvå ⇒ y (x) = 0,8391 x - 0,0000522xtvå
b) Startpunkten väljs vid koordinatsystemets ursprung (0,0):
x (t) = xeller +voxe.t = 400'cos 40º.t = 306,42. t.
y (t) = yeller +vHallå.t -½g.ttvå= 400 'sin 40º.t - 0.5 '9.8'ttvå= 257,12 t - 4,9.ttvå
c) För att hitta den tid projektilen varar i luften, gör y (t) = 0, eftersom lanseringen görs på plan mark:
0 = 257.12.t - 4.9.ttvå
t = 257,12 / 4,9 s = 52,473 s
Den maximala horisontella räckvidden hittas genom att ersätta detta värde i x (t):
xmax = 306,42'52, 47 m = 16077,7 m
Ett annat sätt att hitta xmax direkt är genom att göra y = 0 i banans ekvation:
0 = 0,8391 xmax - 0,0000522 xtvåmax
x = 0,8391 / 0,0000522 m = 16078,5 m
Det finns en liten skillnad på grund av avrundning av decimaler.
d) För att hitta höjden när x = 12000 m, ersätts detta värde direkt i banans ekvation:
och (12000) = 0,8391'12000 - 0,0000522'12000två m = 2552,4 m
Positionsfunktionen för ett objekt ges av:
r (t) = 3t i + (4 -5ttvå) j m
Hitta:
a) Ekvationen för banan. Vilken kurva är?
b) Startpositionen och positionen när t = 2 s.
c) Förskjutningen efter t = 2 s.
a) Positionsfunktionen har givits i termer av enhetsvektorerna i Y j, som bestämmer riktningen på axlarna x Y Y, Således:
x (t) = 3t
och t) = 4 -5ttvå
Banens ekvation y (x) rensar t från x (t) och ersätta i y (t):
t = x / 3
y (x) = 4-5. (x / 3)två = 4 - 5xtvå/ 9 (liknelse)
b) Startpositionen är: r (2) = 4 j m ; positionen i t = 2 s det är r (2) = 6 i -16 j m
c) Förskjutning Dr är subtraktion av de två positionsvektorerna:
Δr = r (två) - r (2) = 6 i -16 j- 4 j = 6 i - tjugo j m
Jorden har en radie R = 6300 km och det är känt att rotationsperioden för dess rörelse runt sin axel är en dag. Hitta:
a) Ekvationen för en punkt på jordytan och dess positionsfunktion.
b) Den punktens hastighet och acceleration.
a) Positionsfunktionen för vilken punkt som helst i cirkulär bana är:
r (t) = R.cos ωt i + R.sen ωt j
Vi har jordens radie R, men inte vinkelhastigheten ω, men den kan beräknas från perioden med vetskap om att för cirkulär rörelse är det giltigt att säga att:
ω = 2π × frekvens = 2π / period
Rörelseperioden är: 1 dag = 24 timmar = 1440 minuter = 86400 sekunder, därför:
ω = 2π / 86400 s = 0,000023148 s-1
Byte i positionsfunktionen:
r (t) = R.cos ωt i + R. sen ωt j = 6300 (cos 0,000023148t i + sen 0,000023148t j) Km
Banan i parametrisk form är:
x (t) = 6300. cos 0.000023148t
y (t) = 6300. sin 0,000023148t
b) För cirkulär rörelse, storleken på den linjära hastigheten v av en punkt är relaterad till vinkelhastigheten w genom:
v = ωR = 0,000023148 s-1'6300 Km = 0.1458 Km / s = 145.8 m / s
Även vara en rörelse med konstant hastighet på 145,8 m / s, det finns en acceleration som pekar mot mitten av den cirkulära banan, med ansvar för att hålla punkten i rotation. Det är den centripetala accelerationen tillc, getts av:
tillc = vtvå / R = (145,8 m / s)två / 6300 × 103 m = 0,00337 m / stvå.
Ingen har kommenterat den här artikeln än.