
Liksidiga triangelegenskaper, egenskaper, formler, area
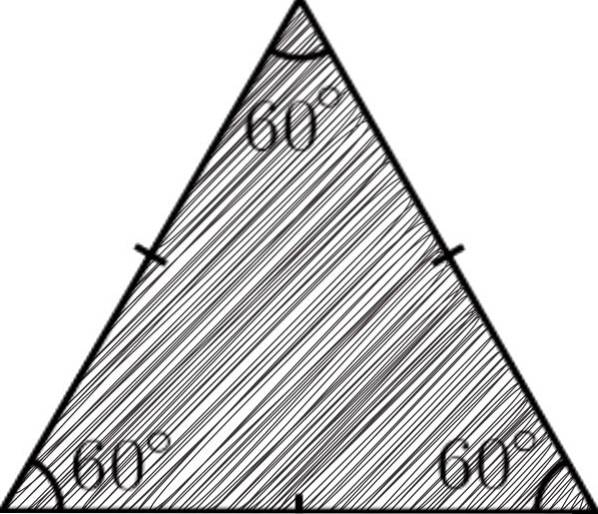
A liksidig triangel det är en polygon med tre sidor, där alla är lika; de har samma mått. För denna egenskap fick den namnet på liksidig (lika sidor).
Trianglar är polygoner som anses vara de enklaste i geometri, eftersom de består av tre sidor, tre vinklar och tre hörn. När det gäller den liksidiga triangeln, eftersom den har lika sidor, innebär det att dess tre vinklar också kommer att vara lika..
Artikelindex
- 1 Egenskaper för liksidiga trianglar
- 1.1 - Lika sidor
- 1.2 - Komponenter
- 2 fastigheter
- 2.1 Inre vinklar
- 2.2 Yttre vinklar
- 2.3 Summan av sidorna
- 2.4 Kongruenta sidor
- 2.5 Kongruenta vinklar
- 3 Hur man beräknar omkretsen?
- 4 Hur man beräknar höjden?
- 5 Hur man beräknar sidorna?
- 6 Hur man beräknar ytan?
- 7 övningar
- 7.1 - Första övning
- 7.2 - Andra övningen
- 7.3 - Tredje övningen
- 8 Referenser
Egenskaper för liksidiga trianglar
- Lika sidor
Liksidiga trianglar är plana och stängda figurer, som består av tre linjesegment. Trianglar klassificeras efter deras egenskaper, i förhållande till deras sidor och vinklar; jämsidan klassificerades med hjälp av måttet på dess sidor som en parameter, eftersom dessa är exakt samma, det vill säga de är kongruenta.
Den liksidiga triangeln är ett särskilt fall av den likbeniga triangeln eftersom två av dess sidor är kongruenta. Det är därför alla liksidiga trianglar också är likbeniga, men inte alla likbenta trianglar kommer att vara liksidiga.
På detta sätt har liksidiga trianglar samma egenskaper som en likbent triangel..
Liksidiga trianglar kan också klassificeras av bredden på deras inre vinklar som en liksidig akut triangel, som har tre sidor och tre inre vinklar med samma mått. Vinklarna kommer att vara akuta, det vill säga de kommer att vara mindre än 90eller.
- Komponenter (redigera)
Trianglar har i allmänhet flera rader och punkter som utgör den. De används för att beräkna arean, sidorna, vinklarna, medianen, halvan, halvan och höjden..
- Median: är en linje som börjar från mittpunkten på ena sidan och når motsatt toppunkt. De tre medianerna konvergerar vid en punkt som kallas barycenter eller centroid..
- Bisektris: det är en stråle som delar vinklarna på hörnpunkterna i två lika stora vinklar, det är därför det är känt som symmetriaxeln. Den liksidiga triangeln har tre symmetriaxlar. I den liksidiga triangeln dras halveringen från toppens vinkel till dess motsatta sida och skär den vid dess mittpunkt. Dessa möts vid en punkt som kallas incenter.
- Mediatrisen: är ett segment vinkelrätt mot den sida av triangeln som har sitt ursprung i mitten av den. Det finns tre läkare i en triangel och de möts vid en punkt som kallas omcentret.
- Höjden: är linjen som går från toppunkten till den motsatta sidan och även denna linje är vinkelrät mot den sidan. Alla trianglar har tre höjder som sammanfaller vid en punkt som kallas ortocentret..
I följande graf ser vi en skalantriangel där några av de nämnda komponenterna är detaljerade
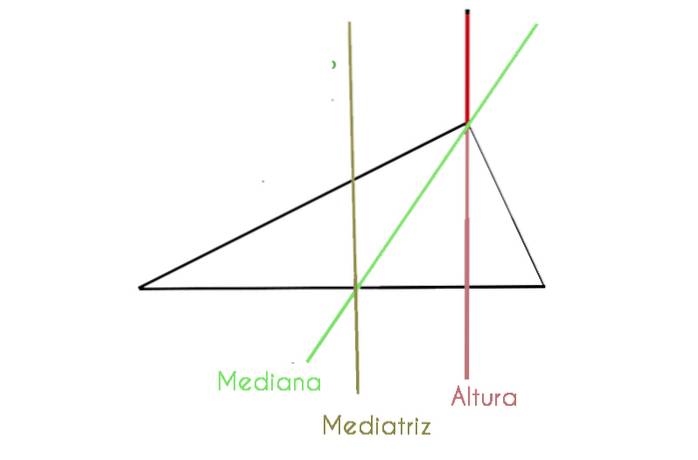
Halvkorsningen, medianen och korsningen är sammanfallande
Halvkanten delar sidan av en triangel i två delar. I liksidiga trianglar kommer den sidan att delas i två exakt lika delar, det vill säga triangeln kommer att delas in i två kongruenta högra trianglar.
Således sammanfaller halvan som är tagen från vilken vinkel som helst i en liksidig triangel med medianen och halvan på sidan motsatt den vinkeln..
Exempel:
Följande bild visar triangeln ABC med en mittpunkt D som delar en av dess sidor i två segment AD och BD.
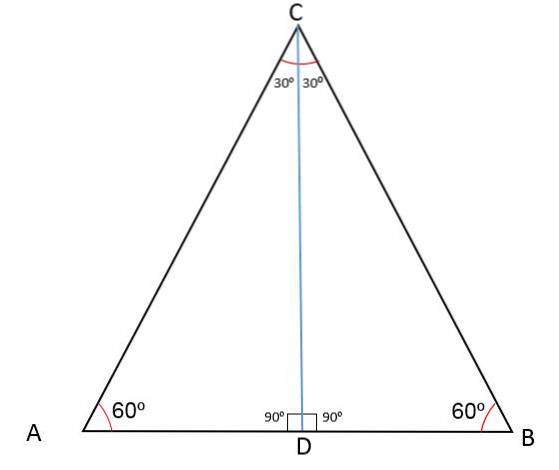
Genom att rita en linje från punkt D till motsatt topp, erhålls per definition median-CD, som är relativt toppunkt C och sida AB.
Eftersom segmentet CD delar triangeln ABC i två lika stora trianglar CDB och CDA, betyder det att fallet med kongruens kommer att uppnås: sida, vinkel, sida och därför kommer CD också att vara en del av BCD.
Plotsegment CD delar toppvinkeln i två lika stora vinklar på 30eller, vinkeln på vertex A mäter fortfarande 60eller och linje-CD: n bildar en vinkel på 90eller med avseende på mittpunkten D.
Segmentet CD bildar vinklar som har samma mått för trianglarna ADC och BDC, det vill säga de är kompletterande på ett sådant sätt att måttet på var och en blir:
Med. (ADB) + Med. (ADC) = 180eller
två * Med. (ADC) = 180eller
Med. (ADC) = 180eller ÷ 2
Med. (ADC) = 90eller.
Och så har vi att segmentet CD också är en del av sidan AB.
Halvkorsningen och höjden är sammanfallande
Genom att dra halvan från toppunkten i en vinkel till mittpunkten på motsatt sida delar den den liksidiga triangeln i två kongruenta trianglar.
På ett sådant sätt att en vinkel på 90 bildaseller (rätt). Detta indikerar att det linjesegmentet är helt vinkelrätt mot den sidan, och per definition skulle linjen vara höjden.
På detta sätt sammanfaller halvan av en vinkel i en liksidig triangel med höjden relativt motsatt sida av den vinkeln..
Ortocenter, barycenter, incenter och sammanfallande circumcenter
Eftersom höjden, medianen, halvan och halvan representeras av samma segment samtidigt, i en liksidig triangel kommer mötespunkterna för dessa segment - ortocentret, halvan, incenteret och cirkumentret - att hittas vid samma punkt:
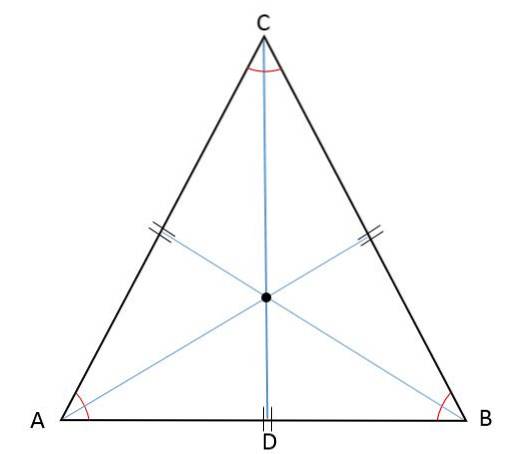
Egenskaper
Huvudegenskapen för liksidiga trianglar är att de alltid kommer att vara likbenta trianglar, eftersom likbeniga bildas av två kongruenta sidor och liksidiga av tre..
På detta sätt ärvde de liksidiga trianglarna alla egenskaperna för den likbeniga triangeln:
Inre vinklar
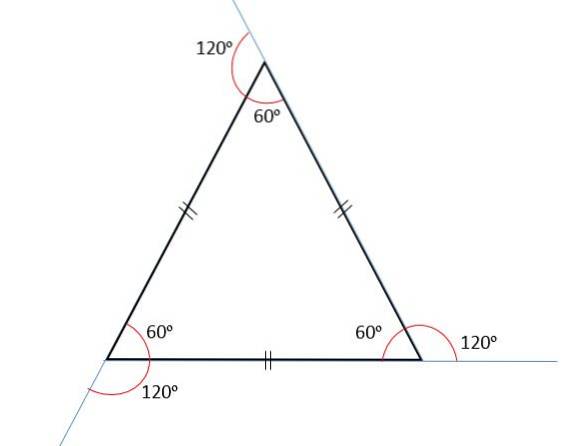
Summan av de inre vinklarna är alltid lika med 180eller, och eftersom alla dess vinklar är kongruenta, kommer var och en av dessa att mäta 60eller.
Yttre vinklar
Summan av de yttre vinklarna kommer alltid att vara 360eller, därför mäter varje yttre vinkel 120eller. Detta beror på att de inre och yttre vinklarna är kompletterande, det vill säga när de läggs till kommer de alltid att vara lika med 180eller.
Summan av sidorna
Summan av måtten på två sidor måste alltid vara större än måttet på den tredje sidan, det vill säga a + b> c, där a, b och c är måtten på varje sida.
Kongruenta sidor
Liksidiga trianglar har alla tre sidor med samma mått eller längd; det vill säga de är kongruenta. Därför har vi i föregående artikel att a = b = c.
Kongruenta vinklar
Liksidiga trianglar är också kända som likvinklade trianglar, eftersom deras tre inre vinklar är kongruenta med varandra. Detta beror på att alla dess sidor också har samma mått.
Hur man beräknar omkretsen?
En polygons omkrets beräknas genom att lägga till sidorna. Som i det här fallet har den liksidiga triangeln alla sidor med samma mått, dess omkrets beräknas med följande formel:
P = 3 * sida.
Hur man beräknar höjden?
Eftersom höjden är linjen vinkelrätt mot basen delar den den i två lika delar genom att sträcka sig till motsatt toppunkt. Så här bildas två lika högra trianglar.
Höjden (h) representerar det motsatta benet (a), hälften av sidan AC till det intilliggande benet (b) och sidan BC representerar hypotenusen (c).
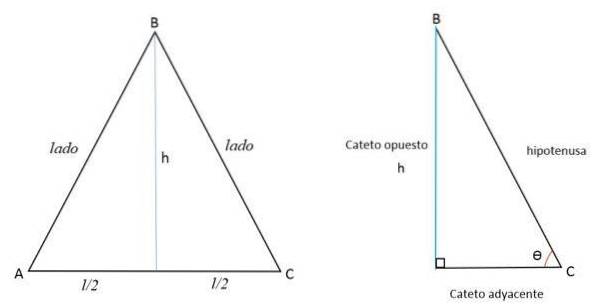
Med Pythagoras sats kan värdet på höjden bestämmas:
tilltvå + btvå = ctvå
Var:
tilltvå = höjd (h).
btvå = sida b / 2.
ctvå = sida a.
Genom att ersätta dessa värden i Pythagoras sats och lösa höjden har vi:
htvå + ( l / två)två = ltvå
htvå + ltvå/ 4 = ltvå
htvå = ltvå - ltvå/ 4
htvå = (4*ltvå - ltvå) / 4
htvå = 3*ltvå /4
√htvå = √ (3*ltvå /4)

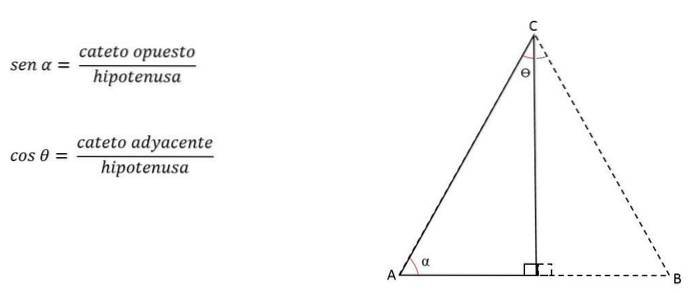
Om vinkeln som bildas av de kongruenta sidorna är känd, kan höjden (representerad av ett ben) beräknas genom att använda de trigonometriska förhållandena.
Benen kallas motsatta eller intilliggande beroende på vinkeln som referens..
Till exempel, i figuren ovan kommer benet h att vara motsatt för vinkel C, men intill vinkel B:
Således kan höjden beräknas med:
Hur man beräknar sidorna?
Det finns fall där måtten på sidorna av triangeln inte är kända, utan deras höjd och vinklarna som bildas i topparna.
För att bestämma området i dessa fall är det nödvändigt att tillämpa trigonometriska förhållanden.
Genom att känna till vinkeln på en av dess hörn identifieras benen och motsvarande trigonometriska förhållande används:
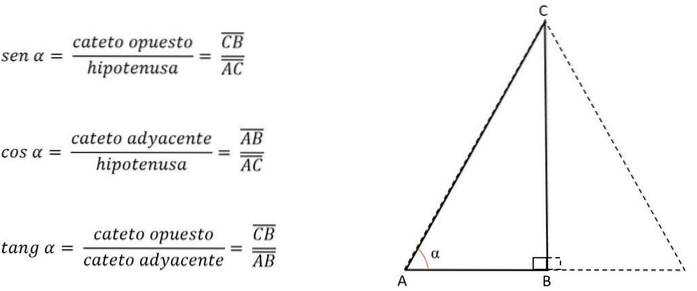
Ben AB kommer således att vara motsatt för vinkel C, men intill vinkel A. Beroende på sidan eller benet som motsvarar höjden rensas den andra sidan för att få sitt värde, med vetskap om att i en liksidig triangel kommer de tre sidorna alltid att ha samma mätning.
Hur man beräknar ytan?
Trianglarnas yta beräknas alltid med samma formel, multiplicerar basen gånger höjden och divideras med två:
Area = (b * h) ÷ 2
Att veta att höjden ges av formeln:

Träning
- Första övningen
Sidorna på en liksidig triangel ABC är 20 cm vardera. Beräkna höjden och arean för den polygonen.
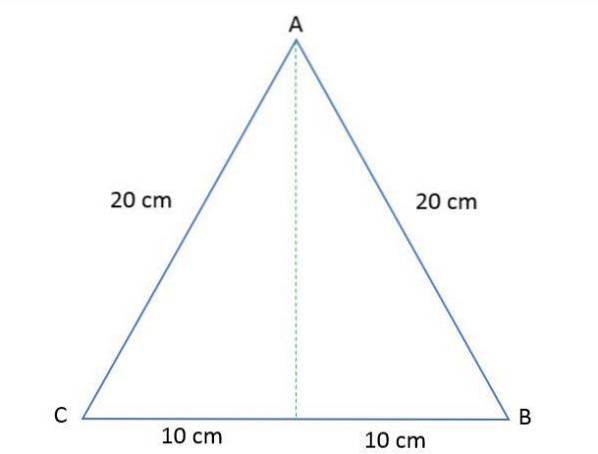
Lösning
För att bestämma ytan för denna liksidiga triangel är det nödvändigt att beräkna höjden, med vetskap om att när du ritar den delar den triangeln i två lika högra trianglar.
På detta sätt kan Pythagoras sats användas för att hitta den:
tilltvå + btvå = ctvå
Var:
a = 20/2 = 10 cm.
b = höjd.
c = 20 cm.
Uppgifterna ersätts i satsen:
10två + btvå = 20två
100 cm + btvå = 400 cm
btvå = (400 - 100) cm
btvå = 300 cm
b = √300 cm
b = 17,32 cm.
Det vill säga att triangelns höjd är 17,32 cm. Nu är det möjligt att beräkna ytan för den givna triangeln genom att ersätta i formeln:
Area = (b * h) ÷ 2
Area = (20 cm * 17,32 cm) ÷ 2
Yta = 346,40 cmtvå ÷ 2
Yta = 173,20 cmtvå.
Ett annat enklare sätt att lösa övningen är att ersätta data i den direkta formeln för området, där höjdens värde också finns implicit:

- Andra övningen
Blommor kommer att planteras på en mark som har formen av en liksidig triangel. Om landets omkrets är lika med 450 m, beräkna antalet kvadratmeter som blommorna kommer att uppta.
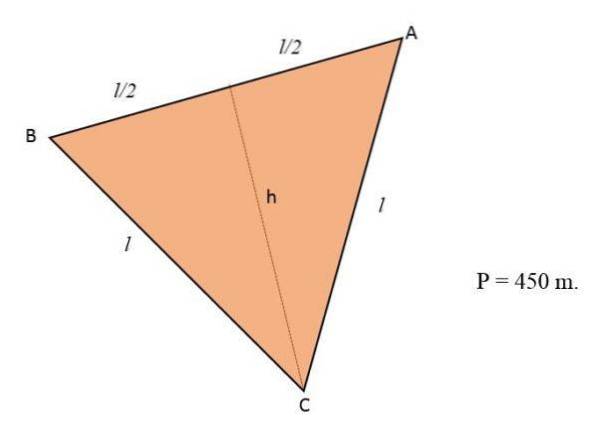
Lösning
Att veta att omkretsen av en triangel motsvarar summan av dess tre sidor och eftersom terrängen har formen av en liksidig triangel, kommer de tre sidorna av denna att ha samma mått eller längd:
P = sida + sida + sida = 3 * l
3 * l = 450 m.
l = 450 m ÷ 3
l = 150 m.
Nu är det bara nödvändigt att beräkna höjden på den triangeln.
Höjden delar triangeln i två kongruenta högra trianglar, där ett ben representerar höjden och den andra halvan basen. Med Pythagoras sats kan höjden bestämmas:
tilltvå + btvå = ctvå
Var:
till = 150 m ÷ 2 = 75 m.
c = 150 m.
b = höjd
Uppgifterna ersätts i satsen:
(75 m)två + btvå = (150 m)två
5.625 m + btvå = 22 500 m
btvå = 22.500 m - 5.625 m
btvå = 16,875 m
b = √16,875 m
b = 129,90 m.
Således kommer det område som blommorna kommer att uppta att vara:
Area = b * h ÷ 2
Area = (150 m * 129,9 m) ÷ 2
Yta = (19.485 mtvå) ÷ 2
Yta = 9 742,5 mtvå
- Tredje övningen
Den liksidiga triangeln ABC divideras med ett linjesegment som går från dess toppunkt C till mittpunkten D, belägen på motsatt sida (AB). Detta segment mäter 62 meter. Beräkna arean och omkretsen för den liksidiga triangeln.
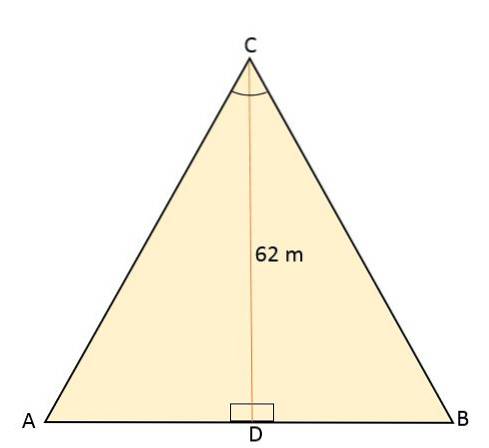
Lösning
Att veta att den liksidiga triangeln divideras med ett linjesegment som motsvarar höjden och därigenom bildar två kongruenta högra trianglar, detta i sin tur delar också vinkeln på toppunkt C i två vinklar med samma mått, 30eller varje.
Höjden bildar en vinkel på 90eller med avseende på segment AB och vinkeln på vertex A kommer då att mäta 60eller.
Använd sedan vinkeln 30 som referenseller, höjd-CD: n är inställd som benet intill vinkeln och BC som hypotenus.
Från dessa data kan värdet på en av sidorna i triangeln bestämmas med hjälp av de trigonometriska förhållandena:
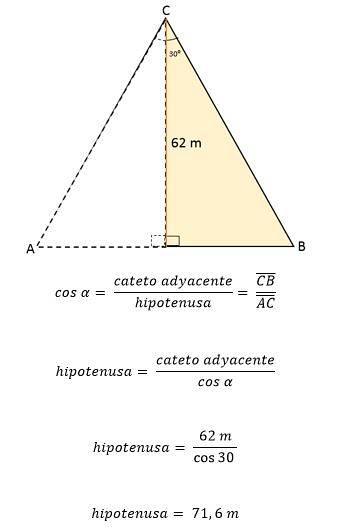
Eftersom i den liksidiga triangeln har alla sidor exakt samma mått eller längd betyder det att varje sida av den liksidiga triangeln ABC är lika med 71,6 meter. Att veta att det är möjligt att bestämma dess område:
Area = b * h ÷ 2
Area = (71,6 m * 62 m) ÷ 2
Yta = 4438,6 mtvå ÷ 2
Area = 2 219,3 mtvå
Omkretsen ges av summan av dess tre sidor:
P = sida + sida + sida = 3 * l
P = 3*l
P = 3 * 71,6 m
P = 214,8 m.
Referenser
- Álvaro Rendón, A. R. (2004). Teknisk ritning: aktivitetsbok.
- Arthur Goodman, L. H. (1996). Algebra och trigonometri med analytisk geometri. Pearson Education.
- Baldor, A. (1941). Algebra. Havanna: Kultur.
- BARBOSA, J. L. (2006). Plan euklidisk geometri. SBM. Rio de Janeiro, .
- Coxford, A. (1971). Geometri En transformationsstrategi. USA: Laidlaw Brothers.
- Euclid, R. P. (1886). Euclids element för geometri.
- Héctor Trejo, J. S. (2006). Geometri och trigonometri.
- León Fernández, G. S. (2007). Integrerad geometri. Metropolitan Technological Institute.
- Sullivan, J. (2006). Algebra och trigonometri. Pearson Education.
Ingen har kommenterat den här artikeln än.