
Normal vektorberäkning och exempel
De normal vektor är den som definierar riktningen vinkelrätt mot någon geometrisk enhet som övervägs, som kan vara en kurva, ett plan eller en yta, till exempel.
Det är ett mycket användbart koncept för positionering av en rörlig partikel eller någon yta i rymden. I följande graf är det möjligt att se hur den normala vektorn till en godtycklig kurva är C:
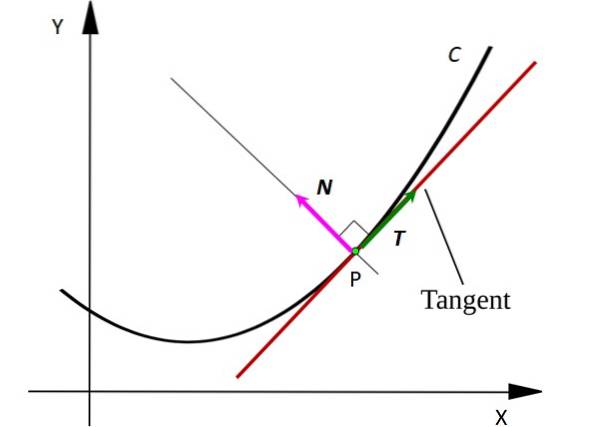
Tänk på en punkt P på kurvan C. Poängen kan representera en rörlig partikel som rör sig längs en C-formad bana. Tangentlinjen till kurvan vid punkt P ritas i rött..
Lägg märke till att vektorn T är tangent till C vid varje punkt, medan vektorn N är vinkelrätt mot T y pekar på mitten av en imaginär cirkel vars båge är ett segment av C. Vektorer betecknas med fet stil i tryckt text för att skilja dem från andra icke-vektormängder.
Vektoren T den indikerar alltid var partikeln rör sig, därför indikerar den dess hastighet. Istället vektorn N pekar alltid i riktningen i vilken partikeln roterar, på detta sätt indikerar den konkaviteten för kurvan C.
Artikelindex
- 1 Hur man tar den normala vektorn till ett plan?
- 1.1 Den normala vektorn från vektorprodukten
- 2 Exempel
- 2.1 Lösning
- 2.2 Beräkning av vektorprodukten AB x AC
- 3 Referenser
Hur man tar den normala vektorn till ett plan?
Den normala vektorn är inte nödvändigtvis en enhetsvektor, det vill säga en vektor vars modul är 1, men i så fall kallas den normal enhetsvektor.
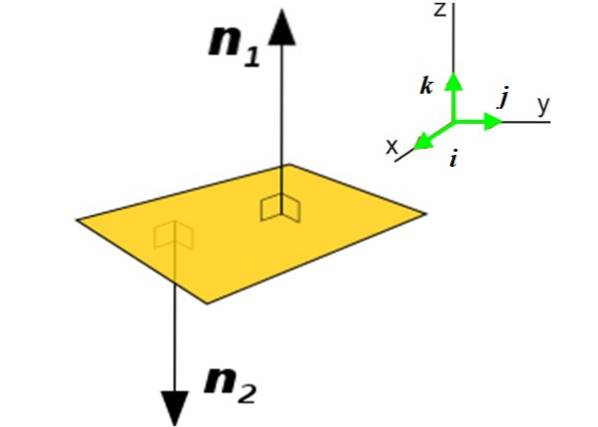
I många applikationer är det nödvändigt att känna till den normala vektorn till ett plan istället för en kurva. Denna vektor avslöjar orienteringen av nämnda plan i rymden. Tänk till exempel på planet P (gul) i figuren:
Det finns två normala vektorer i detta plan: n1 Y ntvå. Användningen av den ena eller den andra beror på det sammanhang i vilket nämnda plan finns. Att få den normala vektorn till ett plan är väldigt enkelt om du känner till dess ekvation:
ax + med + cz + d = 0, med till, b, c Y d riktiga nummer.
Tja, en normal vektor till nämnda plan ges av:
N = a i + b j + c k
Här vektorn N Det uttrycks i termer av enhetsvektorerna och vinkelrätt mot varandra i, j Y k, riktad längs de tre riktningarna som bestämmer utrymmet X och Z, se bild 2 till höger.
Den normala vektorn från vektorprodukten
En mycket enkel procedur för att hitta den normala vektorn använder egenskaperna hos vektorprodukten mellan två vektorer.
Som känt bestämmer tre olika punkter och inte kollinära med varandra ett plan P. Nu är det möjligt att erhålla två vektorer eller Y v som hör till nämnda plan som har dessa tre punkter.
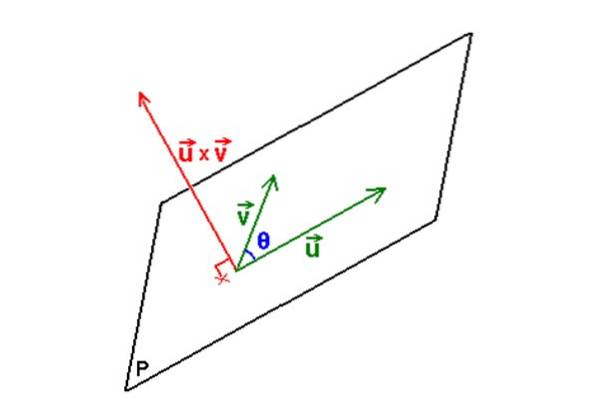
När du väl har vektorerna, vektor produkt eller x v är en operation vars resultat i sin tur är en vektor, som har egenskapen att vara vinkelrät mot det plan som bestäms av eller Y v.
Känd denna vektor betecknas den som N, och från det kommer det att vara möjligt att bestämma ekvationen av planet tack vare ekvationen som anges i föregående avsnitt:
N = eller x v
Följande bild illustrerar det beskrivna förfarandet:
Exempel
Hitta ekvationen för planet bestämt av punkterna A (2,1,3); B (0,1,1); C (4,2,1).
Lösning
Denna övning illustrerar förfarandet som beskrivs ovan. Genom att ha tre punkter väljs en av dem som det gemensamma ursprunget för två vektorer som tillhör det plan som definieras av dessa punkter. Exempelvis ställs punkt A som ursprung och vektorerna är konstruerade AB Y AC.
Vektoren AB är vektorn vars ursprung är punkt A och vars slutpunkt är punkt B. Vektorens koordinater AB bestäms genom att subtrahera koordinaterna för B från koordinaterna för A:
AB = (0-2) i + (1-1) j + (1-3) k = -2i + 0j -två k
Vi fortsätter på samma sätt för att hitta vektorn AC:
AC = (4-2) i + (2-1) j + (1-3) k = 2i + j -två k
Beräkning av vektorprodukten AB x AC
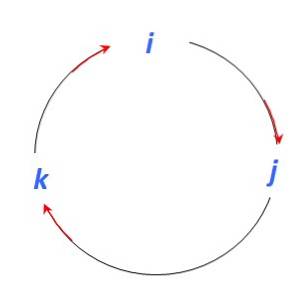
Det finns flera förfaranden för att hitta vektorprodukten mellan två vektorer. I detta exempel används en mnemonisk procedur som använder följande bild för att hitta vektorprodukterna mellan enhetsvektorerna i, j Y k:
Till att börja med är det bra att komma ihåg att vektorprodukterna mellan parallella vektorer är noll, därför:
i x i = 0; j x j = 0; k x k = 0
Och eftersom vektorprodukten är en annan vektor vinkelrätt mot de deltagande vektorerna, när vi rör oss i riktning mot den röda pilen har vi:
i x j = k ; j x k = i; k x i = j
Om du måste flytta i motsatt riktning till pilen lägger du till ett tecken (-):
j x i = - k; k x j = -i; i x k = -j
Totalt är det möjligt att göra 9 vektorprodukter med enhetsvektorerna i, j Y k, varav 3 kommer att vara noll.
AB x AC = (-2i + 0j -två k) x (2i + j -två k) = -4 (i x i) -två (i x j) +4 (i x k) +0 (j x i) + 0 (j x j) - 0 (j x k) - 4 (k x i) -två (k x j) + 4 (k x k) = -2k-4j-4j+tvåi = 2i -8j-tvåk
Ekvation av planet
Vektorn N har bestämts av den tidigare beräknade vektorprodukten:
N = tvåi -8j-tvåk
Därför är a = 2, b = -8, c = -2, det sökta planet:
ax + av + cz + d = 0 → 2x-8y-2z + d = 0
Värdet av d. Detta är lätt om värdena för någon av punkterna A, B eller C som är tillgängliga ersätts i ekvationen av planet. Att välja C till exempel:
x = 4; y = 2; z = 1
Resterna:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
Kort sagt är den sökte kartan:
2x-8y-2z +10 = 0
Den nyfikna läsaren kanske undrar om samma resultat skulle ha uppnåtts istället för att göra AB x AC de skulle ha valt att genomföra AC x AB. Svaret är ja, planet bestämt av dessa tre punkter är unikt och har två normala vektorer, som visas i figur 2.
När det gäller den punkt som väljs som vektorernas ursprung finns det inget problem att välja någon av de andra två.
Referenser
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB). 31- 62.
- Hitta det normala till ett plan. Återställd från: web.ma.utexas.edu.
- Larson, R. (1986). Kalkyl och analytisk geometri. Mc Graw Hill. 616 - 647.
- Linjer och plan i R 3. Återställs från: math.harvard.edu.
- Normal vektor. Återställd från mathworld.wolfram.com.

Ingen har kommenterat den här artikeln än.