
Gratisvektoregenskaper, exempel, övningar
De fria vektorer De är de som är helt specificerade av sin storlek, sin riktning och deras känsla, utan att det är nödvändigt att ange en applikationspunkt eller ett visst ursprung.
Eftersom oändliga vektorer kan ritas på detta sätt är en fri vektor inte en enda enhet utan en uppsättning parallella och identiska vektorer som är oberoende av var de är..
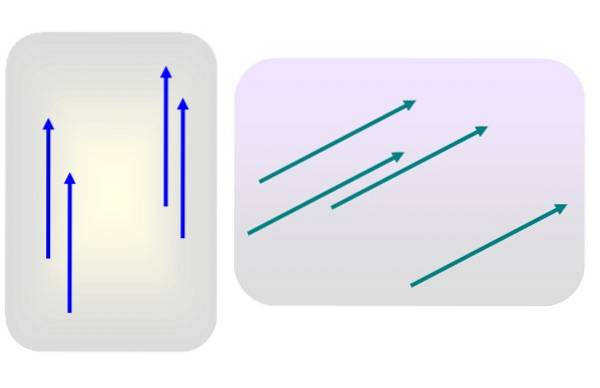
Låt oss säga att vi har flera vektorer av magnitud 3 riktade vertikalt uppåt, eller av magnitude 5 och lutade åt höger, som i figur 1.
Ingen av dessa vektorer används specifikt vid någon tidpunkt. Då är någon av de blå eller gröna vektorerna representativ för deras respektive grupp, eftersom deras egenskaper - modul, riktning och känsla - inte förändras alls när de överförs till en annan plats i planet..
En fri vektor betecknas vanligtvis i tryckt text med exempelvis en fet bokstav v. Eller med gemener och en pil ovanpå om det är handskriven text.
Artikelindex
- 1 Exempel
- 1.1 Egenskaper och egenskaper
- 2 Lösta övningar
- 2.1-Övning 1
- 2.2 Övning 2
- 3 Referenser
Exempel
Fördelen med fria vektorer är att de kan flyttas genom planet eller genom rymden och bibehålla sina egenskaper, eftersom alla representanter för uppsättningen är lika giltiga.
Därför används de ofta i fysik och mekanik. För att till exempel ange linjär hastighet för ett fast ämne är det inte nödvändigt att välja en viss punkt på objektet. Så hastighetsvektorn beter sig som en fri vektor.
Ett annat exempel på en fri vektor är kraftsparet. A par Den består av två krafter av samma storlek och riktning, men av motsatta riktningar, applicerade vid olika punkter på ett fast ämne. Effekten av ett par är inte att översätta objektet utan att orsaka en rotation tack vare ögonblick produceras.
Figur 2 visar ett par krafter som appliceras på en ratt. Genom krafterna F1 Y Ftvå, vridmoment skapas som vrider svänghjulet runt centrum och medurs.
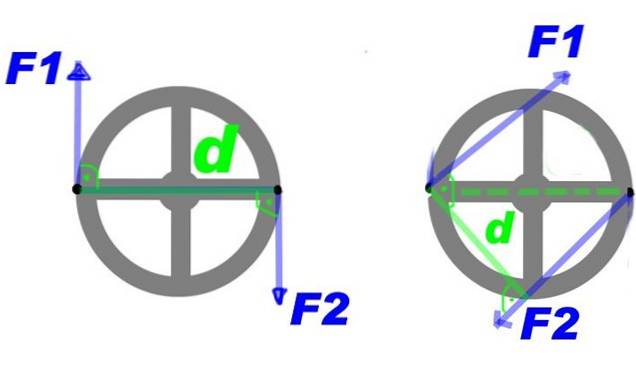
Du kan göra några ändringar i vridmomentet och ändå få samma roterande effekt, till exempel att öka kraften, men minska avståndet mellan dem. Eller behåll kraften och avståndet, men använd vridmomentet på ett annat par punkter på ratten, det vill säga vrid vridmomentet runt mitten.
Momentet för kraftsparet eller helt enkelt par, är en vektor vars modul är Fd och riktas vinkelrätt mot svänghjulets plan. I exemplet som visas enligt konventionen har rotation medurs en negativ känsla.
Egenskaper och egenskaper
Till skillnad från den fria vektorn v, vektorerna AB Y CD de är fixerade (se figur 3), eftersom de har en angiven startpunkt och ankomstpunkt. Men eftersom de är lagmjuka mot varandra och i sin tur med vektorn v, är representativa för den fria vektorn v.

De viktigaste egenskaperna hos fria vektorer är följande:
-Vilken vektor som helst AB (se figur 2) är som sagt representativ för den fria vektorn v.
-Modulen, riktningen och känslan är desamma i alla representanter för den fria vektorn. I figur 2, vektorerna AB Y CD representerar den fria vektorn v och de är laginriktade.
-Med en punkt P i rymden är det alltid möjligt att hitta en representant för den fria vektorn v vars ursprung är i P och representanten är unik. Detta är den viktigaste egenskapen hos fria vektorer och den som gör dem så mångsidiga.
-En nullfri vektor betecknas som 0 y är uppsättningen av alla vektorer som saknar storlek, riktning och känsla.
-Om vektorn AB representerar fri vektor v, sedan vektorn BA representerar fri vektor -v.
-Notationen kommer att användas V3 att beteckna uppsättningen av alla fria vektorer av rymd och Vtvå att utse alla fria vektorer i planet.
Lösta övningar
Med fria vektorer kan följande operationer utföras:
-Belopp
-Subtraktion
-Multiplikation av skalär med en vektor
-Skalarprodukt mellan två vektorer.
-Korsa produkten mellan två vektorer
-Linjär kombination av vektorer
Och mer.
-Övning 1
En student försöker simma från en punkt vid en flod till en annan som ligger mittemot. För att uppnå detta, inget direkt med en hastighet på 6 km / h, i en vinkelrät riktning, men strömmen har en hastighet på 4 km / h som avböjer den.
Beräkna simmarens resulterande hastighet och hur mycket han avböjs av strömmen.
Lösning
Simmarens resulterande hastighet är vektorsumman av hans hastighet (med avseende på floden, ritad vertikalt uppåt) och flodens hastighet (ritad från vänster till höger), som utförs som anges i figuren nedan:
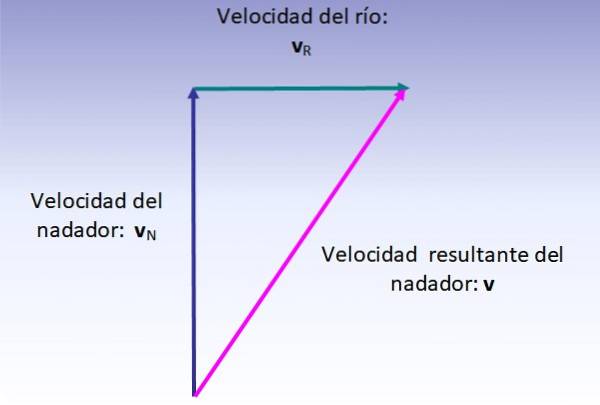
Storleken på den resulterande hastigheten motsvarar hypotenusen för den högra triangeln som visas, därför:
v = (6två + 4två) ½ km / h = 7,2 km / h
Riktningen kan beräknas med vinkeln i förhållande till vinkelrätt mot stranden:
α = arctg (4/6) = 33,7º eller 56,3º i förhållande till stranden.
Övning 2
Hitta ögonblicket för paret som visas i figuren:
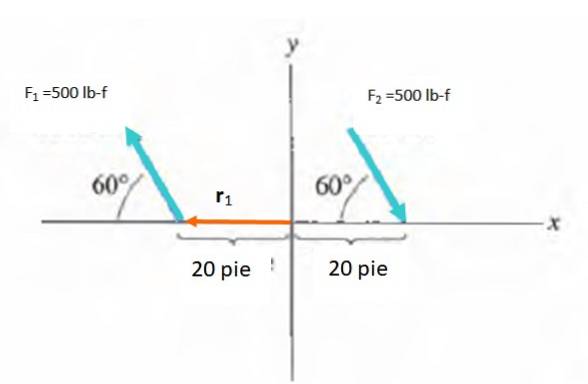
Lösning
Momentet beräknas av:
M = r x F
För närvarande är enheterna lb-f.ft. Eftersom vridmomentet ligger i skärmplanet riktas ögonblicket vinkelrätt mot det, antingen utåt eller inåt..
Eftersom vridmomentet i exemplet tenderar att rotera föremålet som det appliceras på (vilket inte visas i figuren) medurs anses detta ögonblick peka mot insidan av skärmen med ett negativt tecken.
Momentets storlek är M = F.d. i a, där a är vinkeln mellan kraften och vektorn r. Du måste välja en punkt för att beräkna ögonblicket, som är en fri vektor. Därför väljs referenssystemets ursprung r går från O till tillämpningspunkten för varje kraft.
M1 = Mtvå = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. fot
Nettomomentet är summan av M.1 och Mtvå: -17329,5 lb-f. fot.
Referenser
- Beardon, T. 2011. En introduktion till vektorer. Hämtad från: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D.-serien: Fysik för vetenskap och teknik. Volym 1. Kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Återställd från: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. 6: e upplagan. Continental Publishing Company. 15-53.
- Vector Addition Calculator. Återställd från: 1728.org
- Vektorer. Återställd från: en.wikibooks.org



Ingen har kommenterat den här artikeln än.