
Axiell belastning hur den beräknas och övningar löses
De axiell belastning Det är kraften som är riktad parallellt med symmetriaxeln för ett element som utgör en struktur. Den axiella kraften eller belastningen kan vara spänning eller kompression. Om handlingslinjen för den axiella kraften sammanfaller med symmetriaxeln som passerar genom det betraktade elementets centrum, sägs det vara en koncentrisk axiell belastning eller kraft.
Tvärtom, om det är en axiell kraft eller belastning parallell med symmetriaxeln, men vars handlingslinje inte är på själva axeln, är det en excentrisk axiell kraft.
-
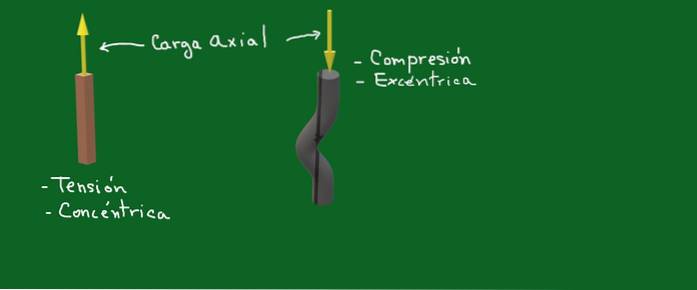
Figur 1. Axiell belastning. Källa: självtillverkad
I figur 1 representerar de gula pilarna axiella krafter eller belastningar. I det ena fallet är det en koncentrisk spänningskraft och i det andra har vi att göra med en excentrisk kompressionskraft.
Måttenheten för axiell belastning i det internationella SI-systemet är Newton (N). Men andra kraftenheter som kilokraft (kg-f) och pundkraft (lb-f) används också ofta..
Artikelindex
- 1 Hur beräknas det?
- 1.1 Förhållande mellan axiell belastning och normal belastning
- 2 Lösta övningar
- 2.1-Övning 1
- 2.2-Övning 2
- 3 Referenser
Hur beräknas det?
För att beräkna värdet på den axiella belastningen i elementen i en struktur måste följande steg följas:
- Gör kraftdiagrammet för varje element.
- Tillämpa ekvationerna som garanterar translationell jämvikt, det vill säga att summan av alla krafter är noll.
- Tänk på ekvationen av vridmoment eller moment så att rotationsjämvikt uppnås. I detta fall måste summan av alla vridmoment vara noll.
- Beräkna krafterna och identifiera krafterna eller axiella belastningarna i vart och ett av elementen.
Förhållandet mellan axiell belastning och normal belastning
Genomsnittlig normal spänning definieras som förhållandet mellan axiell belastning dividerat med tvärsnittsarea. Enheterna för normal ansträngning i International System S.I. de är Newton över kvadratmeter (N / m²) eller Pascal (Pa). Följande figur 2 illustrerar begreppet normal stress för tydlighetens skull..
-
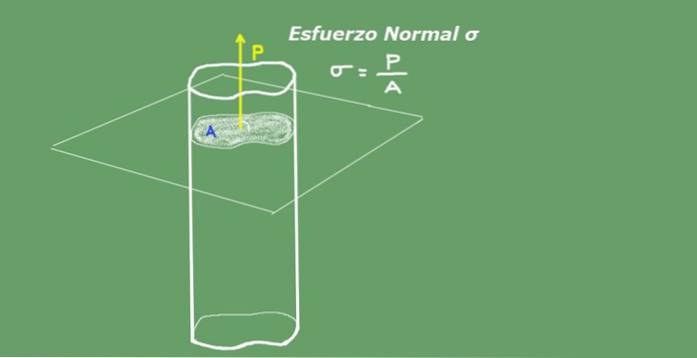
Figur 2. Normal stress. Källa: självtillverkad.
Lösta övningar
-Övning 1
Tänk på en cylindrisk betongpelare med höjd h och radie r. Antag att betongens densitet är ρ. Kolonnen stöder inte någon ytterligare belastning än sin egen vikt och stöds på en rektangulär bas.
- Hitta värdet på den axiella belastningen vid punkterna A, B, C och D, som är i följande positioner: A vid basen av kolonnen, B a ⅓ av höjd h, C a ⅔ av höjd h och senast D vid högst upp i kolumnen.
- Bestäm också den genomsnittliga normala spänningen vid var och en av dessa positioner. Ta följande numeriska värden: h = 3m, r = 20cm och ρ = 2250 kg / m³
-
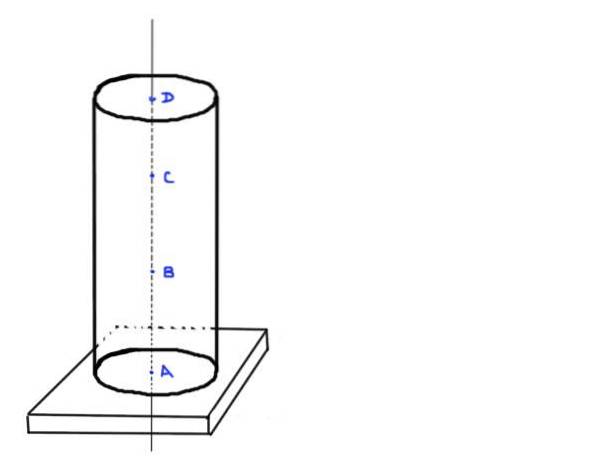
Figur 3. Cylindrisk kolonn. Källa: självtillverkad.
Lösning
Total kolonnvikt
Kolonnens totala vikt W är produkten av densitet gånger volymen multiplicerad med tyngdacceleration:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Axiell belastning i A
Vid punkt A måste kolonnen bära sin fulla vikt, så den axiella belastningen vid denna punkt är kompression är lika med kolonnens vikt:
PA = W = 8313 N
Axiell belastning vid B
Endast ⅔ av kolumnen kommer på punkt B, så den axiella belastningen vid den punkten kommer att vara kompression och dess värde ⅔ kolonnens vikt:
PB = ⅔ W = 5542 N
Figur 3. Cylindrisk kolonn. Källa: självtillverkad.
Ovanför läge C finns bara ⅓ av kolumnen, så dess axiella kompressionsbelastning kommer att ha ⅓ av sin egen vikt:
PC = ⅓ W = 2771 N
Axiell belastning i D
Slutligen finns det ingen belastning på punkt D, som är den övre änden av kolonnen, så den axiella kraften vid den punkten är noll..
PD = 0 N.
Normala ansträngningar i var och en av positionerna
För att bestämma den normala spänningen i var och en av positionerna är det nödvändigt att beräkna tvärsnittet av område A, vilket ges av:
A = π ∙ r² = 0,126 m²
På detta sätt kommer den normala spänningen i var och en av positionerna att vara kvoten mellan den axiella kraften i var och en av punkterna dividerat med det beräknade tvärsnittsområdet, vilket i denna övning är detsamma för alla punkter eftersom det är en kolumn cylindrisk.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Övning 2
Figuren visar en struktur som består av två staplar som vi kommer att kalla AB och CB. Stång AB stöds i änden A av en stift och i den andra änden ansluten till den andra stången med en annan stift B.
På samma sätt stöds stången CB vid änden C med hjälp av en stift och i slutet B med stift B som förbinder den med den andra stången. En vertikal kraft eller belastning F appliceras på stift B som visas i följande bild:
-
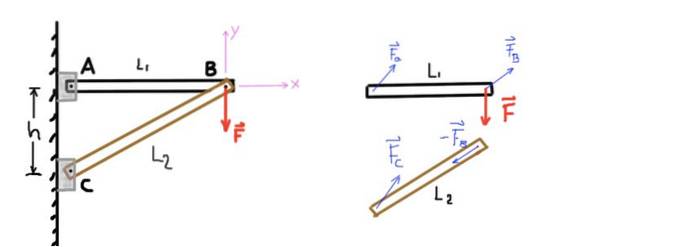
Figur 4. Tvåstångsstruktur och frikroppsdiagram. Källa: självtillverkad.
Antag att stångernas vikt är försumbar, eftersom kraften F = 500 kg-f är mycket större än strukturens vikt. Separationen mellan stöd A och C är h = 1,5 m och längden på stången AB är L1 = 2 m. Bestäm axiell belastning på vart och ett av stängerna, och ange om det är kompression eller axiell belastning.
Lösning 2
Figuren visar, med hjälp av ett frikroppsdiagram, de krafter som verkar på vart och ett av strukturelementen. Det kartesiska koordinatsystemet med vilket kraftjämviktsekvationerna kommer att upprättas anges också..
Moment eller moment kommer att beräknas vid punkt B och kommer att betraktas som positiva om de pekar bort från skärmen (Z-axeln). Balansen mellan krafter och vridmoment för varje stång är:
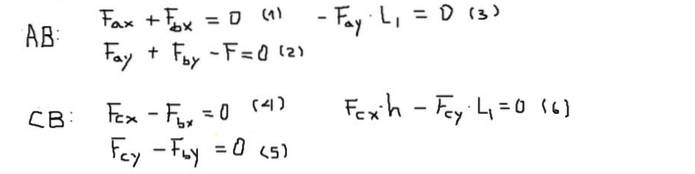
Därefter löses komponenterna i krafterna i var och en av ekvationerna i följande ordning:
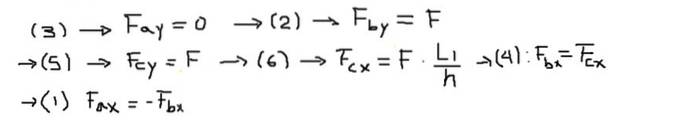
Slutligen beräknas de resulterande krafterna i slutet av varje stapel:
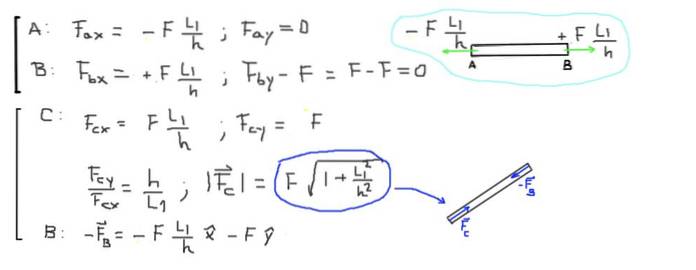
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
Stången CB är i kompression på grund av de två krafterna som verkar vid dess ändar som är parallella med stången och pekar mot dess centrum. Storleken på den axiella kompressionskraften i stapeln CB är:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Referenser
- Öl F ... Mekanik av material. 5: e. Utgåva. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Materialmekanik. Åttonde upplagan. Prentice Hall. 2011. 3-60.
- Gere J. Materialmekanik. Åttonde upplagan. Cengage Learning. 4-220.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e upplagan Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Anteckningar om allmän fysik. UNAM. 87-98.



Ingen har kommenterat den här artikeln än.