
Oelastisk kraschar i en dimension och exempel
De oelastiska chocker eller oelastiska kollisioner är en kort och intensiv interaktion mellan två objekt i vilka momentet bevaras, men inte den kinetiska energin, av vilken en procentandel omvandlas till någon annan typ av energi.
Kraschar eller kollisioner är vanliga. Subatomära partiklar kolliderar i extremt höga hastigheter, medan många sporter och spel består av kontinuerliga kollisioner. Även galaxer kan kollidera.

I verkligheten bevaras momentum i alla typer av kollisioner, så länge de kolliderande partiklarna bildar ett isolerat system. Så i den meningen är det inga problem. Nu har objekt kinetisk energi associerad med den rörelse de har. Vad kan hända med den energin när du kolliderar??
De inre krafterna som sker under kollisionen mellan föremål är starka. När det anges att kinetisk energi inte bevaras betyder det att den omvandlas till andra typer av energi: till exempel till ljudenergi (en spektakulär kollision har ett distinkt ljud).
Fler användningsmöjligheter för kinetisk energi: friktionsvärme och naturligtvis den oundvikliga deformationen som föremål genomgår vid kollision, såsom karosserna i bilarna i figuren ovan.
Artikelindex
- 1 Exempel på oelastiska kollisioner
- 2 Perfekt oelastiska kollisioner i en dimension
- 3 Restitutionskoefficient
- 4 Hur man bestämmer återbetalningskoefficienten?
- 5 arbetade exempel
- 5.1-Övning 1
- 5.2-Övning 2
- 5.3-Övning 3
- 6 Referenser
Exempel på oelastiska kollisioner
- Två massor av plasticine kolliderar och klibbar ihop, rör sig som en bit efter kollisionen.
- En gummikula som studsar av en vägg eller ett golv. Bollen deformeras när den träffar ytan.
Inte all kinetisk energi omvandlas till andra typer av energi, med få undantag. Objekt kan hålla en viss mängd av denna energi. Senare kommer vi att se hur man beräknar procentandelen.
När kollideringsstyckena hänger ihop kallas kollisionen helt oelastisk och båda tenderar att röra sig tillsammans..
Perfekt oelastiska kollisioner i en dimension
Kollisionen i figuren visar två objekt av olika massor m1 Y mtvå, rör sig mot varandra med hastigheter vi1 Y vi2 respektive. Allt händer horisontellt, det vill säga det är en kollision i en dimension, den enklaste att studera.
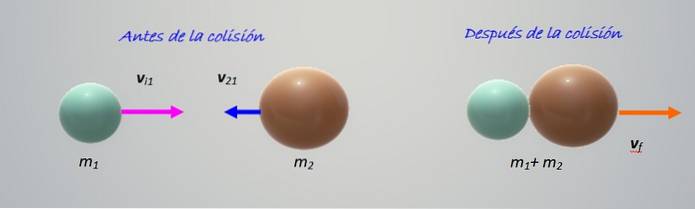
Objekten kolliderar och klibbar sedan ihop genom att flytta till höger. Det är en helt oelastisk kollision, så vi måste bara hålla fart:
Peller = PF
Momentum är en vektor vars SI-enheter är N.s. I den beskrivna situationen kan vektornotationen undvikas när man hanterar kollisioner i en dimension:
mveller = mvF
Systemets momentum är vektorsumman för varje partikels momentum.
m1 vi1 + mtvå vi2 = (m1 + mtvå) vF
Den slutliga hastigheten ges av:
vF = (m1 vi1 + mtvå vi2) / (m1 + mtvå)
Restitutionskoefficient
Det finns en mängd som kan indikera hur elastisk en kollision är. Det handlar om återbetalningskoefficient, som definieras som den negativa kvoten mellan partiklarnas relativa hastighet efter kollisionen och den relativa hastigheten före kollisionen.
Låt oss1 och dutvå respektive hastigheter hos partiklarna initialt. Och var v1 och Vtvå respektive sluthastigheter. Matematiskt kan restitutionskoefficienten uttryckas enligt följande:
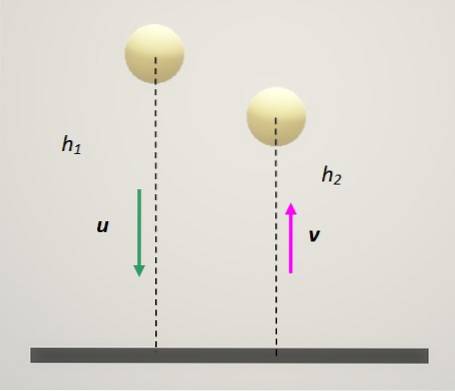
- Om ε = 0 motsvarar det att bekräfta att vtvå = v1. Det betyder att sluthastigheterna är desamma och kollisionen är oelastisk, som den som beskrivs i föregående avsnitt..
- När ε = 1 betyder det att de relativa hastigheterna både före och efter kollisionen inte ändras, i detta fall är kollisionen elastisk.
- Och om 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
Hur man bestämmer återbetalningskoefficienten?
Restitutionskoefficienten beror på vilken materialklass som är involverad i kollisionen. Ett mycket intressant test för att bestämma hur elastiskt ett material är för att göra kulor är att släppa bollen på en fast yta och mäta reboundhöjden.

I det här fallet har den fasta plattan alltid hastighet 0. Om den tilldelas index 1 och kulindexet 2 är:
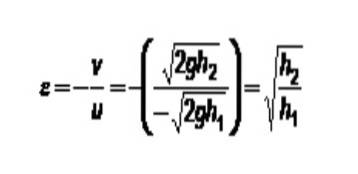



I början har det föreslagits att all kinetisk energi kan omvandlas till andra typer av energi. Trots allt förstörs inte energi. Är det möjligt att rörliga föremål kolliderar och förenas för att bilda ett enda objekt som plötsligt vilar? Detta är inte så lätt att föreställa sig.
Låt oss dock föreställa oss att det händer tvärtom, som i en film sett i omvänd ordning. Så objektet var först i vila och exploderade sedan och splittrades i olika delar. Denna situation är fullt möjlig: det är en explosion.
Så en explosion kan betraktas som en perfekt oelastisk kollision sett tillbaka i tiden. Drivkraften bevaras också, och det kan sägas att:
Peller = PF
Arbetade exempel
-Övning 1
Det är känt från mätningar att återställningskoefficienten för stål är 0,90. En stålkula släpps från en höjd av 7 m på en fast platta. Beräkna:
a) Hur hög kommer den att studsa.
b) Hur lång tid tar det mellan den första kontakten med ytan och den andra.
Lösning
a) Ekvationen som härleddes i avsnittet om bestämning av restitutionskoefficienten används:
Höjden rensas htvå:
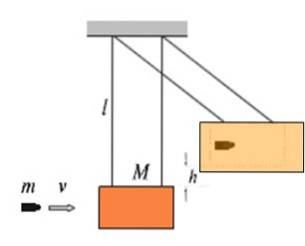
0,90två . 7 m = 5,67 m
b) För att den ska stiga 5,67 meter krävs en hastighet som ges av:


t max = veller/ g = (10,54 / 9,8 s) = 1,08 s.
Tiden det tar att återvända är densamma, därför är den totala tiden att klättra 5,67 meter och återvända till startpunkten två gånger den maximala tiden:
tflyg = 2,15 s.
-Övning 2
Figuren visar ett träblock med massa M som hänger i vila av strängar med längden l som en pendel. Detta kallas en ballistisk pendel och används för att mäta hastigheten v för inträde i en kula med massa m. Ju högre hastighet med vilken kulan träffar blocket, desto högre h kommer den att stiga.
Kulan i bilden är inbäddad i blocket, därför är det en helt oelastisk chock.

Anta att en 9,72-g-kula träffar massan med massa 4,60 kg, sedan stiger enheten 16,8 cm från jämvikt. Vad är hastigheten v från kulan?
Lösning
Under kollisionen bevaras drivkraften och ellerF är hastigheten för hela, när kulan har inbäddat sig i blocket:
Peller = PF
Blocket är initialt i vila, medan kulan riktas mot målet med hastighet v:
m.v + M.0 = (m + M) uF
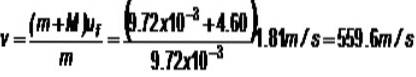
Okänt ellerF fortfarande, men efter kollisionen bevaras den mekaniska energin, detta är summan av gravitationspotentialenergin U och den kinetiska energin K:
Initial mekanisk energi = Slutlig mekanisk energi
OCHmån = Emf
ELLEReller + Keller = UF + KF
Gravitationens potentiella energi beror på höjden som uppsättningen når. För jämviktspositionen är den initiala höjden den som tas som referensnivå, därför:
ELLEReller = 0
Tack vare kulan har hela kinetisk energi Keller, som omvandlas till gravitationspotentialenergi när uppsättningen når sin maximala höjd h. Den kinetiska energin ges av:
K = ½ mvtvå
Ursprungligen är den kinetiska energin:
Keller = (1/2) (M + m) uFtvå
Kom ihåg att kulan och blocket redan bildar ett enda massobjekt M + m. Gravitationspotentialenergin när de har nått sin maximala höjd är:
ELLERF = (m + M) gh
Därför:
Keller = UF
(1/2) (M + m) uFtvå = (m + M) gh
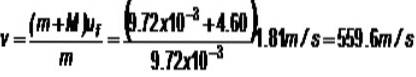
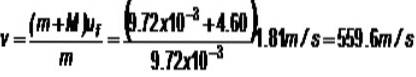
-Övning 3
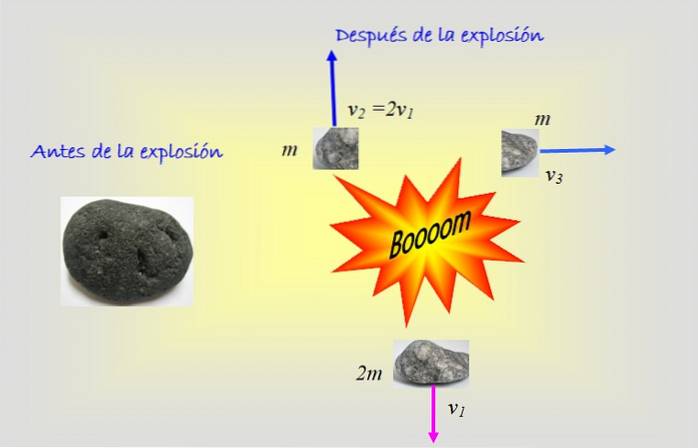
Objektet i figuren exploderar i tre fragment: två med lika massa m och ett större med massa 2 m. Figuren visar hastigheterna för varje fragment efter explosionen. Vad var objektets ursprungliga hastighet?
Lösning
I detta problem krävs användning av två koordinater: x och Y, eftersom två av fragmenten har vertikala hastigheter, medan resten har horisontell hastighet.
Objektets totala massa är summan av massan av alla fragment:
M = m + m + 2m = 4m
Momentet bevaras både i x-axeln och i y-axeln, det anges separat:
- 4m. ellerx= m v3
- 4m. ellerY = m. 2v1 - 2m. v1
Observera att det stora fragmentet rör sig neråt med hastighet v1, för att indikera detta faktum har ett negativt tecken placerats på det.
Från den andra ekvationen följer det omedelbart att ellerY = 0, och från den första rensas ux omedelbart:

Referenser
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6th. Ed Prentice Hall. 175-181
- Rex, A. 2011. Grundläggande fysik. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Cengage Learning. 172-182
- Tipler, P. (2006) Fysik för vetenskap och teknik. 5: e utgåvan Volym 1. Redaktionellt Reverté. 217-238
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. MacGraw Hill. 185-195



Ingen har kommenterat den här artikeln än.