
Jämviktsförhållanden koncept, applikationer och exempel
De jämviktsförhållanden De är nödvändiga för att en kropp ska vara i vila eller i enhetlig rätlinjig rörelse. I det första fallet sägs det att objektet är i statisk jämvikt, medan det i det andra är i dynamisk jämvikt.
Förutsatt att det rörliga objektet är en partikel, i vilket fall dimensionerna inte beaktas, räcker det att summan av krafter som verkar på den annulleras.

Men en stor majoritet av rörliga föremål har märkbara dimensioner, därför är detta tillstånd inte tillräckligt för att garantera jämvikt, vilket i alla fall är frånvaron av acceleration, inte rörelse..
Artikelindex
- 1 Första och andra jämviktsförhållandet
- 2 applikationer
- 2.1 Isostatisk jämvikt
- 2.2 Hur fusion fungerar i kärnan
- 2.3 Konstruktion
- 3 Typer av statisk jämvikt
- 3.1 Stabil jämvikt
- 3.2 Likgiltig eller neutral balans
- 3.3 Instabil jämvikt
- 4 Exempel: partiklarstatik
- 5 Övningen löst
- 5.1 Lösning
- 6 Intressanta ämnen
- 7 Referenser
Första och andra jämviktsförhållandet
Låt oss se: om summan av krafter är noll är det sant att objektet inte kommer att röra sig eller röra sig i en accelererad takt, men det kan fortfarande börja rotera.
För att undvika rotationer måste därför ett andra villkor läggas till: att summan av vridmoment eller vridmoment som orsakas av yttre krafter som verkar på den, runt vilken punkt som helst, också upphävs..
Kort sagt, betecknar som F nettokraftvektorn y τ eller M till nettomomentvektorn har vi:
Första jämviktsförhållandet
∑ F = 0
Vilket innebär att: ∑ Fx = 0, ∑ FY = 0 och ∑ Fz = 0
Andra jämviktsförhållandet
∑ τ = 0 eller ∑ M = 0
Med vridmomenten eller momenten beräknade om vilken punkt som helst.
I det följande antar vi att det rörliga föremålet är en styv kropp, en som inte genomgår någon deformation..
Applikationer
Trots att rörelse verkar vara den gemensamma nämnaren i universum, är balans också närvarande i många aspekter av naturen och i föremålen som omger oss..
Isostatisk jämvikt
I planet skala är jorden inne isostatisk jämvikt, en slags gravitationell balans av jordskorpan, vars densitet inte är enhetlig.
Skillnaderna i densiteterna för de olika blocken eller områdena i jordskorpan kompenseras av höjdskillnaderna som kännetecknar planetens orografi. Det fungerar på samma sätt som olika material är mer eller mindre nedsänkta i vatten enligt deras densitet och når jämvikt.
Men eftersom blocken i skorpan inte flyter ordentligt i vatten utan i manteln, som är mycket mer viskös, kallas inte jämvikten hydrostatisk utan isostatisk..
Hur fusion fungerar i kärnan
I stjärnor som vår sol, håller balansen mellan tyngdkraften som komprimerar dem och det hydrostatiska trycket som expanderar dem, fusionsreaktorn i stjärnans kärna igång, vilket håller den vid liv. Vi är beroende av denna balans för att jorden ska få det ljus och värme som krävs.
Byggnad
I lokal skala vill vi att byggnader och konstruktioner ska förbli stabila, det vill säga följa jämviktsförhållandena, särskilt statisk jämvikt..
Det är därför som statik uppstod, vilket är den gren av mekaniken som är dedikerad till att studera kroppsbalansen och allt som behövs för att hålla dem på det sättet..
Typer av statisk jämvikt
I praktiken finner vi att statisk jämvikt kan vara av tre slag:
Stabil jämvikt
Det inträffar när objektet rör sig från sitt läge och omedelbart återvänder till det när kraften som drev bort det upphör. Ju närmare ett objekt är marken, desto mer sannolikt är det att det är i stabil jämvikt.
Kulan till höger i figur 2 är ett bra exempel, om vi tar bort den från dess jämviktsposition längst ner i skålen, kommer tyngdkraften att ta hand om dess snabba återgång.
Likgiltig eller neutral balans
Det inträffar när objektet, trots att det flyttas, fortfarande är i balans. Runda föremål som bollen, när de placeras på plana ytor, är i likvärdig jämvikt.
Instabil balans
Det inträffar när objektet rör sig från dess jämviktsposition, återgår det inte till det. Om vi flyttar bollen från toppen av backen till vänster är det säkert att den inte kommer tillbaka under sin egen kraft..

Exempel: partikelstatik
Anta ett massblock m på ett lutande plan, av vilket all massa antas koncentreras i sitt geometriska centrum.
Den horisontella delen av vikten Wx det tenderar att få blocket att glida nedför, därför behövs ytterligare en motsatt kraft. Om vi vill att kvarteret ska vara i vila är denna kraft den statiska friktionen. Men om vi låter blocket glida nedåt med konstant hastighet är den kraft som krävs dynamisk friktion..
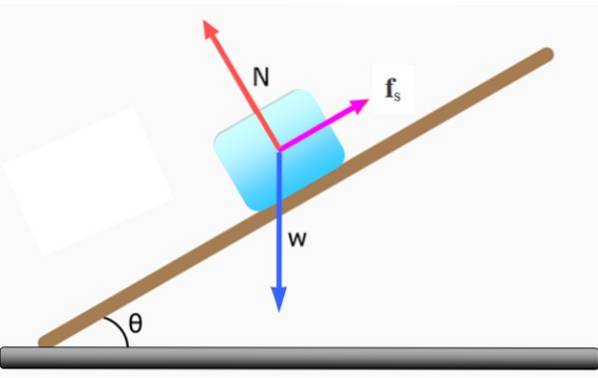
I avsaknad av friktion glider blocket snabbt nedåt och i detta fall kommer det inte att finnas någon jämvikt.
För att blocket ska vara i vila, krafterna som verkar på det: vikt W, det normala N och den statiska friktionen Fs, de måste kompenseras. Sedan:
∑ FY = 0 → N - WY = 0
∑ Fx = 0 → Wx - Fs = 0
Statisk friktion balanserar den horisontella delen av vikten: Wx = fs och därför:
Fs = m. g .sen θ
Övningen löst
Ett 21,5 kg trafikljus hänger från en homogen aluminiumstång AB med en vikt på 12 kg och 7,5 m, uppburen av en horisontell rep-CD, som visas i figuren. Hitta:
a) DC-kabelns spänning
b) De horisontella och vertikala komponenterna i kraften som utövas av svängen A på stolpen.
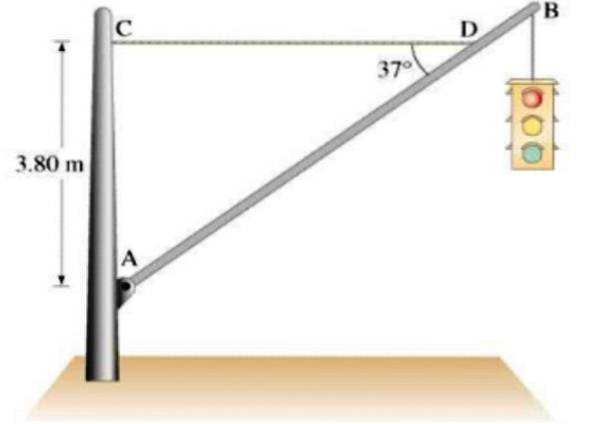
Lösning
Diagrammet över krafter som appliceras på stången konstrueras med vikten W, spänningarna i ackorden och de horisontella och vertikala komponenterna i svängreaktionen, kallad Rx och RY. Då gäller jämviktsförhållandena.
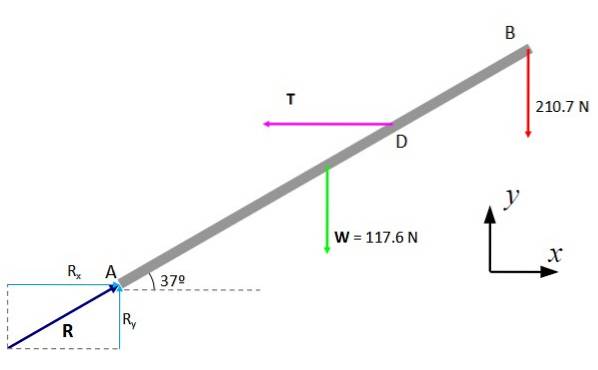
Första villkoret
Att vara ett problem i planet, erbjuder det första jämviktsförhållandet två ekvationer:
ΣFx = 0
ΣFY = 0
Från den första:
Rx - T = 0
Rx = T
Och den andra:
RY - 117,6 N - 210,7 N = 0
RY = 328,3 N
Den horisontella komponenten i reaktionen är lika stor som spänningen T.
Andra villkoret
Punkt A i figur 5 väljs som rotationscentrum, på detta sätt reaktionsarmen R är null, kom ihåg att ögonblickets storlek ges av:
M = F┴ d
Där F┴ är kraftens vinkelräta komponent och d är avståndet mellan rotationsaxeln och kraftens appliceringspunkt. Vi får en ekvation:
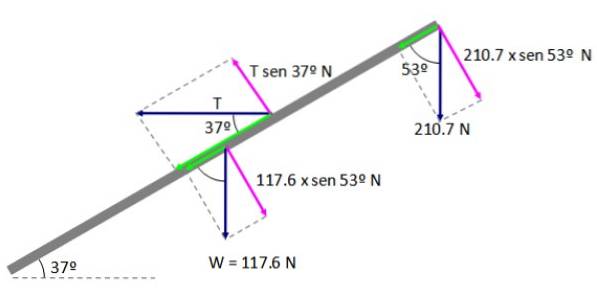
ΣMTILL = 0
(210,7 × sin 53º) AB + (117,6 × sin 53º) (AB / 2) - (T × sin 37º) AD = 0
Avståndet AD är:
AD = (3,8 m / sin 37º) = 6,3 m
(210,7 × sin 53º N) (7,5 m) + (117,6 × sin 53º N) (3,75 m) - (T × sin 37º N) (6,3 m) = 0
Genomföra de angivna operationerna:
1262.04 + 352.20 - 3.8T = 0
Lösning för T får vi:
T = 424,8 N
Från det första tillståndet, Rx = T, därför:
Rx = 424,8 N
Teman av intresse
Första jämviktsförhållandet.
Andra jämviktsförhållandet.
Referenser
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 4. Partikelsystem. Redigerad av Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Utg. Volym 1.
- Wikipedia. Isostasia. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.