
Kalibreringskurva vad den är avsedd för, hur man gör det, exempel

De kalibreringskurva Det är ett diagram som relaterar till två variabler, som används för att verifiera att en mätutrustning fungerar korrekt. Oavsett utrustning påverkar tid, användning och naturligt slitage mätningens kvalitet.
Det är därför det är viktigt att regelbundet verifiera att den fungerar korrekt. Detta görs genom att jämföra mätningarna som tillhandahålls av utrustningen med mätningarna för en standardanordning som används som referens. Denna referensutrustning är den mest exakta.
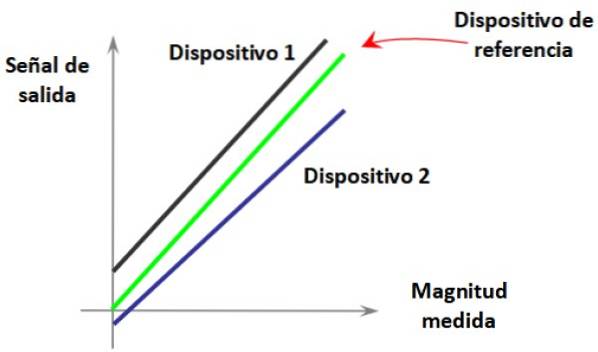
Till exempel, i figur 1 har vi utsignalen från en ideal enhet i grönt, jämfört med den uppmätta storleken, båda är proportionella.
I samma diagram finns kurvorna för två olika instrument som inte är kalibrerade och som har lite olika beteenden från varandra och från standard.
Artikelindex
- 1 Hur fungerar det??
- 2 Hur man gör en kalibreringskurva?
- 2.1 Steg 1
- 2.2 Steg 2
- 2.3 Steg 3
- 2.4 Steg 4
- 3 Exempel på kalibreringskurva
- 3.1 Kalibrering av en platinamotståndstermometer
- 3.2 Kalibreringskurva för en lösning
- 4 Övningen löst
- 4.1 Lösning
- 5 Referenser
Hur fungerar det?
Antag till exempel att vi vill kalibrera en dynamometer, som är en anordning som används för att mäta krafter som föremålens vikt och de som visas när ett objekt accelereras..
För att få en fjäder att sträcka sig är det nödvändigt att applicera en kraft som är proportionell mot sträckan, enligt Hookes lag.
En enkel dynamometer består av en fjäder inuti ett rör utrustat med en pekare och en skala för att indikera sträckning. I ena änden finns en ring för att hålla dynamometern och i den andra en krok för att hänga vikter.
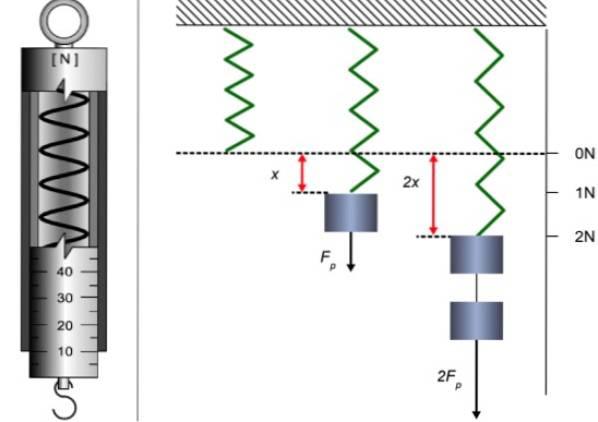
Ett sätt att kalibrera dynamometern är genom att hänga olika vikter, vars massa tidigare bestämdes med en balans (referensinstrumentet) och att mäta fjäderns sträckning eller töjning, som antas vara ljus..
Hookes lag tillämpad på fjädermassasystemet i statisk jämvikt resulterar i följande ekvation, som relaterar fjäderns längd till den hängande massan:
L = (g / k) m + Lo
Var:
-L: fjäderns totala längd
-g: tyngdacceleration
-k: fjäderkonstant
-m: massa
-Lo: naturlig fjäderlängd.
När du har flera par poäng längdmassa, de plottas sedan för att konstruera kalibreringskurvan. Eftersom förhållandet mellan längd L och massa m är linjärt är kurvan en rak linje, där:
Lutning = g / k
Hur man gör en kalibreringskurva?
Det här är stegen för att göra en kalibreringskurva till ett mätinstrument.
Steg 1
Välj den jämförelsestandard som ska användas, beroende på vilken enhet som ska kalibreras.
Steg 2
Välj lämpligt värdeområde och bestäm det optimala antalet mätningar som ska utföras. Om vi skulle kalibrera en dynamometer skulle vi först behöva bedöma gränsen för vikten som kan hängas utan att den deformeras permanent. Om detta skulle hända skulle instrumentet vara oanvändbart.
Steg 3
Ta avläsningspar: den ena är avläsningen gjord med standardmönstret, den andra är mätningen som görs med sensorn som kalibreras.
Steg 4
Gör en graf över de avläsningspar som erhölls i föregående steg. Det kan göras för hand, på grafpapper eller med hjälp av ett kalkylark.
Det senare alternativet är att föredra eftersom spårning för hand kan leda till små felaktigheter, medan en bättre passning kan göras med kalkylbladet..
Exempel på kalibreringskurva
Kalibreringskurvor används också för att konvertera en kvantitet till en annan som är lätt att läsa, genom någon egendom eller lag som relaterar dem..
Kalibrering av en platinamotståndstermometer
Ett alternativ till användning av kvicksilver är elektriskt motstånd. Motstånd är en bra termometrisk egenskap, eftersom den varierar med temperaturen och också är lätt att mäta med en ohmmeter eller amperemätare..
Tja, i det här fallet skulle en lämplig standard för att konstruera kalibreringskurvan vara en bra laboratorietermometer..
Du kan mäta temperatur - motståndspar och ta dem till ett diagram som senare kommer att användas för att bestämma alla temperaturvärden som känner till motståndet, så länge värdet på detta ligger inom mätområdet som har gjorts.
Följande kalibreringskurva visar temperaturen på x-axeln med standardtermometern och temperaturen på den vertikala axeln med en platinamotståndstermometer, kallad termometer A.
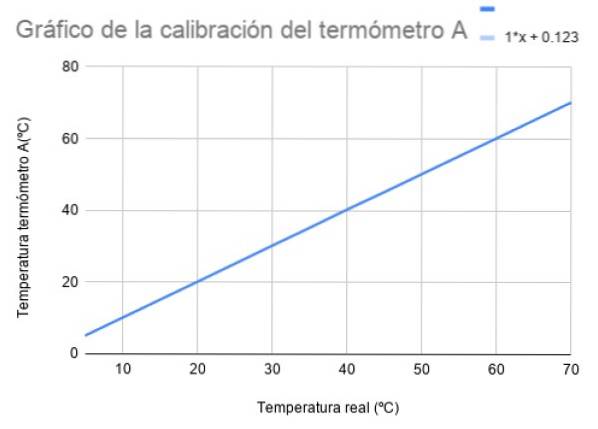
Kalkylarket hittar den linje som bäst passar mätningarna, vars ekvation visas uppe till höger. Platinatermometern har en drift på 0,123 ºC i förhållande till standarden.
Kalibreringskurva för en lösning
Det är en metod som används inom analytisk kemi och består av en referenskurva, där den uppmätta kvantiteten är koncentrationen av en analyt på den horisontella axeln, medan det instrumentella svaret visas på den vertikala axeln, som visas i följande exempel.
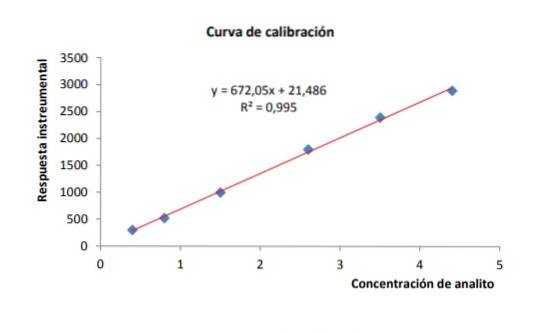
Kurvan används för att genom interpolering hitta koncentrationen av analyt närvarande i ett okänt prov genom nämnda instrumentella svar..
Det instrumentella svaret kan vara en elektrisk ström eller en spänning. Båda mängderna är lätta att mäta i laboratoriet. Kurvan används sedan för att ta reda på koncentrationen av den okända analyten på detta sätt:
Antag att strömmen är 1500 mA på kalibreringskurvan. Vi står på denna punkt på den vertikala axeln och drar en horisontell linje upp till kurvan. Från denna punkt projicerar vi en linje vertikalt mot x-axeln, där respektive koncentration av analyten avläses..
Övningen löst
Konstruera kalibreringskurvan för en fjäder med elastisk konstant k och utifrån diagrammet, bestäm värdet för nämnda konstant, allt baserat på följande experimentella data för längd - masspar:

Lösning
Varje par värden tolkas enligt följande:
När en massa på 1 kg hängs sträcks fjädern till 0,32 m. Om en massa på 2 kg hängs kommer fjädern att mäta 0,40 m och så vidare.
Med hjälp av ett kalkylblad utvecklas diagrammet över längd mot massa, vilket visar sig vara en rak linje, som förväntat från Hookes lag, eftersom förhållandet mellan längd L och massa m ges av:
L = (g / k) m + Lo
Som förklarats i tidigare avsnitt. Grafen som erhålls är följande:
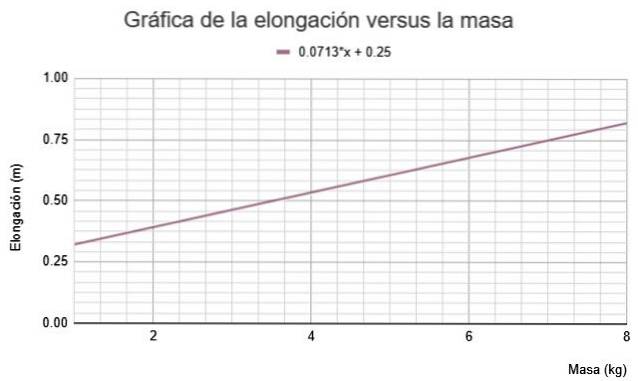
Under rubriken visar kalkylbladet ekvationen för den rad som bäst passar experimentdata:
L = 0,0713 m + 0,25
Linjens skärning med den vertikala axeln är fjäderns naturliga längd:
Leller = 0,25 m
För sin del är lutningen kvoten g / k:
g / k = 0,0713
Därför tar g = 9,8 m / stvå, värdet på fjäderkonstanten är:
k = (9,8 / 0,0713) N / m
k = 137,45 N / m
Med detta värde är vår fjäder kalibrerad och dynamometern redo att mäta krafter på följande sätt: en okänd massa hängs som producerar en viss sträcka, som avläses på den vertikala axeln..
Från detta värde dras en horisontell linje tills den når kurvan och vid den tidpunkten projiceras en vertikal linje till x-axeln där massvärdet avläses. Med massan har vi sin vikt, vilket är den kraft som orsakar förlängningen.
Referenser
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9: e upplagan Cengage Learning.
- Tipler, P. 1987. Fysik före universitetet. Redaktionellt Reverté.
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. Mcgraw hill
- Wilson, J. 2010. Physics Laboratory Experiment. 7: e. Ed Brooks Cole.
- Wikipedia. Kalibreringskurva. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.