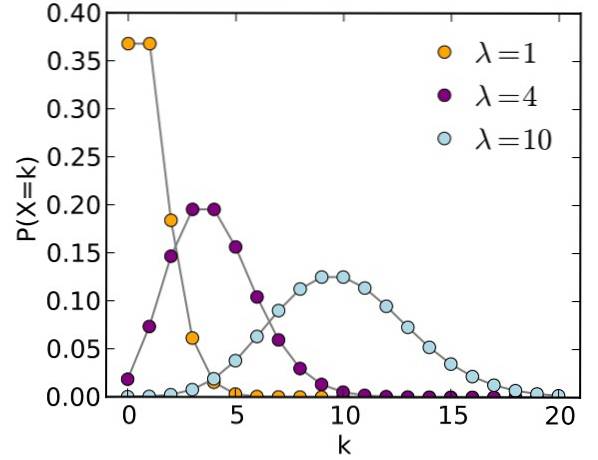
De Poisson distribution är en diskret sannolikhetsfördelning, genom vilken det är möjligt att känna till sannolikheten att inom en stor samplingsstorlek och under ett visst intervall inträffar en händelse vars sannolikhet är liten.
Ofta kan Poisson-fördelningen användas istället för binomialfördelningen, så länge följande villkor är uppfyllda: stort urval och liten sannolikhet.
Siméon-Denis Poisson (1781-1840) skapade denna distribution som bär hans namn, mycket användbar när det gäller oförutsägbara händelser. Poisson publicerade sina resultat 1837, ett forskningsarbete om sannolikheten för felaktiga straffdomar.
Senare anpassade andra forskare fördelningen i andra områden, till exempel antalet stjärnor som kunde hittas i en viss volym, eller sannolikheten att en soldat dog av en hästspark.
Artikelindex
Den matematiska formen av Poisson-fördelningen är som följer:
- μ (även ibland betecknad som λ) är medelvärdet eller parametern för fördelningen
- Euler nummer: e = 2,71828
- Sannolikheten att erhålla y = k är P
- k är antalet framgångar 0, 1,2,3 ...
- n är antalet tester eller händelser (provets storlek)
Diskreta slumpmässiga variabler, som namnet antyder, beror på slump och tar bara diskreta värden: 0, 1, 2, 3, 4 ..., k.
Medelvärdet för fördelningen ges av:
Variansen σ, som mäter spridningen av data, är en annan viktig parameter. För Poisson-distributionen är det:
σ = μ
Poisson bestämde att när n → ∞ och p → 0, så kallas medelvärdet μ -och förväntat värde- tenderar att vara konstant:
μ → konstant
Viktig: sid är sannolikheten för händelsen med hänsyn till den totala befolkningen, medan P (y) är Poisson-förutsägelsen på provet.
Poisson-distributionen har följande egenskaper:
-Provstorleken är stor: n → ∞.
-Händelserna eller händelserna som beaktas är oberoende av varandra och inträffar slumpmässigt.
-Sannolikhet P den vissa händelsen Y inträffar under en viss tidsperiod är mycket liten: P → 0.
-Sannolikheten att fler än en händelse inträffar i tidsintervallet är 0.
-Genomsnittsvärdet är ungefär en konstant som ges av: μ = n.p (n är provstorleken)
-Eftersom dispersionen σ är lika med μ, eftersom den antar större värden, blir variationen också större.
-Händelserna måste fördelas jämnt inom det tidsintervall som används.
-Uppsättningen av möjliga händelsevärden Y är: 0,1,2,3,4 ... .
-Summan av i variabler som följer en Poisson-fördelning, är också en annan Poisson-variabel. Dess genomsnittliga värde är summan av medelvärdena för dessa variabler.
Poisson-fördelningen skiljer sig från binomialfördelningen på följande viktiga sätt:
-Binomialfördelningen påverkas av både provstorleken n och sannolikheten P, men Poisson-fördelningen påverkas bara av medelvärdet μ.
-I en binomial fördelning, de möjliga värdena för den slumpmässiga variabeln Y är 0,1,2,…, N, å andra sidan i Poisson-fördelningen finns det ingen övre gräns för dessa värden.
Poisson tillämpade ursprungligen sin berömda distribution på rättsfall, men på industriell nivå var en av hans tidigaste användningsområden i tillverkningen av öl. I denna process används jästkulturer för jäsning.
Jäst består av levande celler vars befolkning varierar över tiden. Vid tillverkning av öl är det nödvändigt att tillsätta den nödvändiga mängden, därför är det nödvändigt att veta mängden celler som finns per volymenhet.
Under andra världskriget användes Poisson-distributionen för att ta reda på om tyskarna verkligen siktade på London från Calais, eller bara slog av slumpmässigt. Detta var viktigt för de allierade för att avgöra hur bra tekniken var tillgänglig för nazisterna..
Tillämpningarna av Poisson-distributionen hänvisar alltid till räknar i tid eller räknas i rymden. Och eftersom sannolikheten för förekomst är liten är den också känd som "lagen om sällsynta händelser".
Här är en lista över händelser som faller inom en av dessa kategorier:
-Registrering av partiklarna i ett radioaktivt sönderfall, som liksom tillväxten av jästceller, är en exponentiell funktion.
-Antal besök på en viss webbplats.
-Ankomst av människor i en rad för att betala eller delta (köteori).
-Antal bilar som passerar en viss punkt på en väg under ett visst tidsintervall.
-Mutationer i en viss DNA-sträng efter att ha fått strålningsexponering.
-Antalet meteoriter med en diameter större än 1 m föll under ett år.
-Defekter per kvadratmeter tyg.
-Antal blodkroppar i 1 kubikcentimeter.
-Samtal per minut till en telefonväxel.
-Chokladflis i 1 kg kaksmet.
-Antal träd infekterade av en viss parasit i 1 hektar skog.
Observera att dessa slumpmässiga variabler representerar antalet gånger en händelse inträffar under en fast tidsperiod (samtal per minut till telefonväxeln), eller en viss rymdregion (defekter av ett tyg per kvadratmeter).
Dessa händelser är, som redan har fastställts, oberoende av den tid som har gått sedan den senaste händelsen..
Poisson-fördelningen är en bra approximation till binomialfördelningen så länge som:
-Provstorleken är stor: n ≥ 100
-Sannolikhet p är liten: p ≤ 0,1
- μ är i ordningen: np ≤ 10
I sådana fall är Poisson-fördelningen ett utmärkt verktyg, eftersom binomialfördelningen kan vara svår att tillämpa i dessa fall..
En seismologisk studie fastställde att det under de senaste 100 åren fanns 93 stora jordbävningar runt om i världen, åtminstone 6,0 på Richters skala - logaritmisk-. Antag att Poisson-distributionen är en lämplig modell i det här fallet. Hitta:
a) Den genomsnittliga förekomsten av stora jordbävningar per år.
b) Ja P (y) är sannolikheten för händelse Y jordbävningar under ett slumpmässigt utvalt år, hitta följande sannolikheter:
P(0), P(1), P (två), P (3), P (4), P (5), P (6) och P (7).
c) De verkliga resultaten av studien är följande:
- 47 år (0 jordbävningar)
- 31 år (1 jordbävningar)
- 13 år (2 jordbävningar)
- 5 år (3 jordbävningar)
- 2 år (4 jordbävningar)
- 0 år (5 jordbävningar)
- 1 år (6 jordbävningar)
- 1 år (7 jordbävningar)
Hur jämförs dessa resultat med de som erhållits i del b? Är Poisson-distributionen ett bra val för att modellera dessa händelser?
a) Jordbävningar är händelser vars sannolikhet sid den är liten och vi överväger en begränsad tidsperiod på ett år. Det genomsnittliga antalet jordbävningar är:
μ = 93/100 jordbävningar / år = 0,93 jordbävningar per år.
b) För att beräkna de begärda sannolikheterna ersätts värden i formeln i början:
y = 2
μ = 0,93
e = 2,71828
Det är ganska mindre än P (2).
Resultaten listas nedan:
P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.
Vi kan till exempel säga att det finns en sannolikhet på 39,5% att ingen större jordbävning kommer att inträffa under ett visst år. Eller att det finns 5,29% av tre stora jordbävningar som inträffar det året.
c) Frekvenserna analyseras, multiplicerat med n = 100 år:
39,5; 36,7; 17.1; 5,29; 1,23; 0,229; 0,0355 och 0,00471.
Till exempel:
- En frekvens på 39,5 indikerar att, på 39,5 av 100 år, 0 stora jordbävningar inträffar, kan vi säga att det är ganska nära det faktiska resultatet på 47 år utan någon större jordbävning..
Låt oss jämföra ett annat Poisson-resultat med de faktiska resultaten:
- Det erhållna värdet 36,7 betyder att det under en 37-årsperiod sker en stor jordbävning. Det faktiska resultatet är att det på 31 år skedde en större jordbävning, vilket passar bra med modellen.
- 17,1 år förväntas med två stora jordbävningar och det är känt att det på 13 år, vilket är ett nära värde, verkligen fanns två stora jordbävningar.
Därför är Poisson-modellen acceptabel för detta fall.
Ett företag uppskattar att antalet komponenter som misslyckas innan de når 100 driftstimmar följer en Poisson-distribution. Om det genomsnittliga antalet fel är 8 under den tiden, hitta följande sannolikheter:
a) Att en komponent inte fungerar på 25 timmar.
b) Fel på mindre än två komponenter på 50 timmar.
c) Fel på minst tre komponenter på 125 timmar.
a) Det är känt att genomsnittet av fel på 100 timmar är 8, därför förväntas en fjärdedel av fel på 25 timmar, det vill säga 2 fel. Detta kommer att vara parametern μ.
Sannolikheten att 1 komponent misslyckas begärs, den slumpmässiga variabeln är "komponenter som misslyckas före 25 timmar" och dess värde är y = 1. Genom att ersätta sannolikhetsfunktionen:
Frågan är dock hur sannolikt de misslyckas mindre än två komponenter på 50 timmar, inte att exakt två komponenter misslyckas på 50 timmar, därför måste vi lägga till sannolikheten att:
-Ingen misslyckas
-Misslyckas endast 1
P (mindre än 2 komponenter misslyckas) = P (0) + P (1)
P (färre än 2 komponenter misslyckas) = 0,0183 + 0,0732 = 0.0915
c) Att de misslyckas minst 3 komponenter på 125 timmar, betyder att 3, 4, 5 eller mer kan misslyckas under den tiden.
Sannolikheten att det inträffar minst en av flera händelser är lika med 1, minus sannolikheten att ingen av händelserna inträffar.
-Den önskade händelsen är att 3 eller flera komponenter misslyckas på 125 timmar
-Om händelsen inte inträffar betyder det att mindre än tre komponenter misslyckas, vars sannolikhet är: P (0) + P (1) + P (2)
Parametern μ för fördelningen i detta fall är:
μ = 8 + 2 = 10 fel på 125 timmar.
P (3 eller flera komponenter misslyckas) = 1- P (0) - P (1) - P (2) =
Ingen har kommenterat den här artikeln än.