
Kontinuerliga enhetliga fördelningsegenskaper, exempel, tillämpningar
En slumpmässig variabel har en kontinuerlig enhetlig fördelning om sannolikheten att det tar ett värde inom ett begränsat intervall [a, b], är detsamma för varje delintervall med lika längd.
Denna fördelning är analog med den diskreta enhetliga fördelningen, som tilldelade samma sannolikhet för varje resultat av det slumpmässiga experimentet, men i detta fall är variabeln som ska beaktas kontinuerlig. Exempelvis följer experimentet som består av att välja ett reellt tal slumpmässigt, mellan värdena a och b, den enhetliga fördelningen. Här är dess graf:
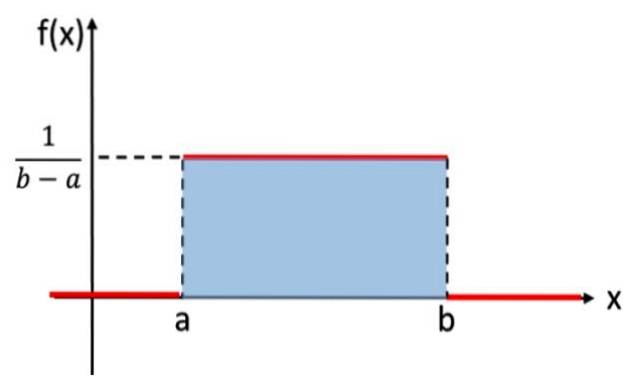
I matematisk notation har den kontinuerliga enhetliga fördelningen en densitetsfunktion definierad som en bitvis eller bitvis funktion, som kan skrivas som:
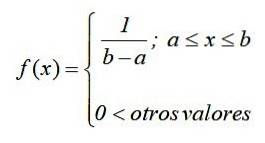
Grafen för denna funktion, känd som densitetskurva eller funktion, är en rektangel, därför är den kontinuerliga enhetliga fördelningen också känd som rektangulär layout y är den enklaste av de kontinuerliga fördelningarna.
Arean under diagrammet för en sannolikhetsfördelning är lika med 1 och tar alltid positiva värden. Den enhetliga fördelningen uppfyller dessa kriterier. Det är inte nödvändigt att integrera direkt för att kontrollera att området är 1, eftersom området för den skuggade rektangeln i figur 1 kan beräknas med formeln:
Area = bas x höjd = (b - a) x [1 / (b - a)] = 1
Att känna till området under densitetskurvan är mycket viktigt, eftersom det finns ett samband mellan området och sannolikheten för att en händelse inträffar, vilket för denna fördelning bestäms i nästa avsnitt.
Kännetecken för kontinuerlig enhetlig distribution
Den kontinuerliga enhetliga fördelningen kännetecknas av dess:
Densitetsfunktion
Låt X vara den kontinuerliga slumpmässiga variabeln, som tillhör intervallet [a, b], sedan:

Distributionsfunktion
Fördelningsfunktionen beräknar sannolikheten att den slumpmässiga variabeln X tar ett värde x bland de möjliga värdena för intervallet [a, b]. För en kontinuerlig distribution beräknas det generellt så här:

I fallet med den kontinuerliga enhetliga fördelningen är sannolikheten F (x) lika med arean av rektangeln vars bas är (x-a) och dess höjd är (b-a):

Matematiskt, om F (x) = Pr (X = x) fastställs följande funktion i delar, enligt föregående resultat:

På detta sätt verifieras det som sagts tidigare: sannolikheten beror bara på värdet på (x-a) och inte på dess placering i intervallet [a, b]. Grafen för fördelningsfunktionen är:
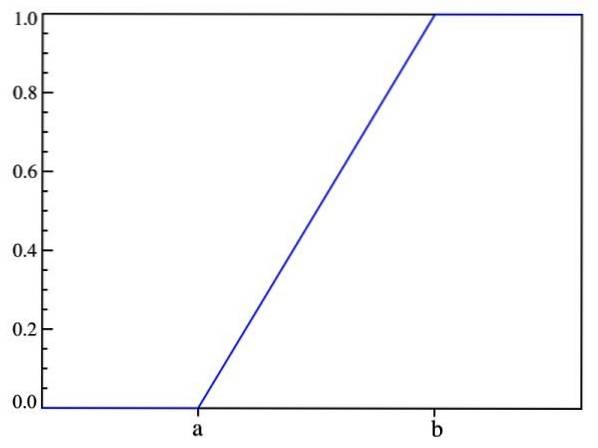
Förväntat värde, avvikelse och standardavvikelse
Efter att ha gjort flera experiment med den kontinuerliga slumpmässiga variabeln kallas dess medelvärde förväntat värde, betecknas som E (X) och beräknas med följande integral:

V (X) = E (Xtvå) - E (X)två
Därför:


D (X) = √ V (X)

Median, läge, symmetri och kurtos
Det kan enkelt verifieras att medianen, som är det centrala värdet för den enhetliga fördelningen, är lika med medelvärdet, och eftersom det inte finns något värde som upprepas mer än andra, eftersom alla är lika troliga i intervallet [a, b] , mode existerar inte.
Beträffande symmetri är den enhetliga fördelningen symmetrisk och kurtosen, vilket är i vilken grad värdena koncentreras runt centrum, är -6/5.
Exempel
Olika situationer kan modelleras genom kontinuerlig distribution, och därmed kan deras beteende förutsägas. Här är några exempel:
Exempel 1
Ett företag som tillhandahåller elservice tillhandahåller spänningsnivåer jämnt fördelade, mellan 123,0 V och 125,0 V. Detta innebär att det i hushållsuttaget är möjligt att få vilket spänningsvärde som helst som hör till det intervallet..
Så, som sett ovan, är grafen för densitetsfunktionen rektangeln i rött:

Att beräkna sannolikheten för att ha en spänning inom det angivna intervallet är mycket lätt, till exempel, vad är sannolikheten för att företaget skickar en spänning lägre än 123,5 V?
Denna sannolikhet är lika med den blå skuggade rektangeln:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
Och vad är sannolikheten för att den levererade spänningen är större än 124,0 V.?
Eftersom den totala ytan är lika med 1 är den eftersträvade sannolikheten:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Det är vettigt, eftersom 124.0 är exakt värdet i mitten av intervallet.
Exempel 2
En viss slumpmässig variabel X har en jämn fördelning i intervallet [0,100]. Besluta:
a) Sannolikheten att värdet på X är mindre än 22.
b) Sannolikheten att X tar värden mellan 20 och 35.
c) Det förväntade värdet, variansen och standardavvikelsen för denna fördelning.
Svara på
Det bestäms på ett liknande sätt som föregående exempel, men först måste vi bestämma höjden på rektangeln och komma ihåg att den totala ytan måste vara lika med 1:
Area = 100 × höjd = 1
Därför har rektangeln en höjd som är lika med 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Svar b
Den begärda sannolikheten är lika med arean av rektangeln vars bredd är (35 - 20) och vars höjd är 0,01:
P (22 Om du föredrar att gå direkt till distributionsfunktionen ovan, måste du bara ersätta värdena i: P (20≤X≤35) = F (35) -F (20) Med F (x) ges av: F (x) = (x-a) / (b-a) Värdena som ska anges är: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 Det förväntade värdet är: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 Variansen är: V (X) = (b-a)två/ 12 = (100-0)två/ 12 = 833,33 Och standardavvikelsen är: D (X) = √833,33 = 28,87 Denna fördelning är användbar när man utför statistiska simuleringsprocesser eller när man arbetar med händelser vars frekvens av förekomst är regelbunden.. Vissa programmeringsspråk genererar slumpmässiga tal mellan 0 och 1, och som framgår av föregående exempel är sannolikhetsfördelningen som följs enhetlig. I detta fall är intervallet att tänka på [0,1]. Om du har ett experiment där händelserna har regelbundenhet, som förklarats tidigare, kan du i princip tilldela var och en samma sannolikhet för händelse. I det här fallet ger den probabilistiska modellen för enhetlig distribution information för analysen.. Den enhetliga fördelningen används också för att avrunda skillnaderna mellan de observerade värdena och de verkliga värdena för en variabel, förutsatt att en enhetlig fördelning av felet i ett givet intervall, enligt avrundning, vanligtvis från -0,5 till +0,5.Svar c
Applikationer
Slumpmässig nummergenerering
Provtagning av godtyckliga fördelningar
Avrundning av fel
Referenser

Ingen har kommenterat den här artikeln än.