De Helmholtz fri energi är en termodynamisk potential som mäter nyttan av ett slutet system under förhållanden med konstant temperatur och volym. Helmholtz fri energi betecknas som F y definieras som skillnaden mellan den inre energin ELLER minus temperaturprodukt T genom entropi S:
F = U - T⋅S
Eftersom det är energi mäts det i Joule in the International System (SI), även om andra lämpliga enheter också kan vara ergs (CGS), kalorier eller elektronvolt (eV).
Den negativa variationen av Helmholtz-energin under en process likställs med det maximala arbete som systemet kan göra i en isokorisk process, det vill säga vid konstant volym. När volymen inte hålls konstant kan en del av detta arbete göras på miljön.
I det här fallet hänvisar vi till arbete där volymen inte varierar, såsom elarbete: dW = Φdq, med Φ som den elektriska potentialen och q som den elektriska laddningen.
Om temperaturen också är konstant minimeras Helmholtz-energin när jämvikt uppnås. För allt detta är Helmholtz-energin särskilt användbar i processer med konstant volym. I det här fallet har du:
- För en spontan process: ΔF < 0
- När systemet är i jämvikt: ΔF = 0
- I en icke-spontan process: ΔF> 0.
Artikelindex
Som anges i början definieras Helmholtz-energin som "systemets inre energi U minus produkten av systemets absoluta temperatur T, av systemets entropi S":
F = U - T⋅S
Det är en funktion av temperatur T och volym V. Stegen för att visualisera detta är som följer:
- Med utgångspunkt från termodynamikens första lag är den inre energin U relaterad till entropin S i systemet och dess volym V för reversibla processer genom följande differentieringsförhållande:
dU = dQ - dW = TdS - PdV
Av detta följer att den interna energin U är en funktion av variablerna S Y V, Således:
U = U (S, V)
- Nu tar vi definitionen av F och det härleds:
dF = dU - d (TS) = dU - TdS - SdT
- Genom att där ersätta det differentiella uttrycket som erhållits för dU i det första steget, förblir det:
dF = TdS - PoV - TdS - SdT = -SdT - PoV
- Slutligen dras slutsatsen att F är en funktion av temperaturen T och volymen V och kan uttryckas som:
F = F (T, V)
Helmholtz-energin kan appliceras som ett allmänt kriterium för spontanitet i isolerade system, men först är det bekvämt att specificera några begrepp:
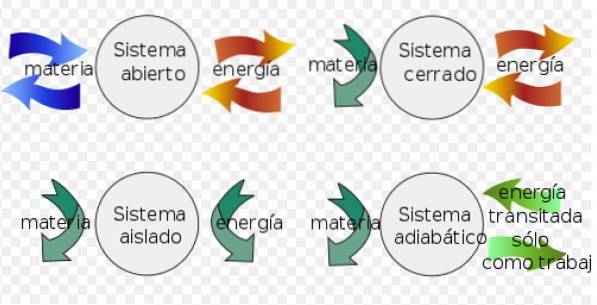
- A systemet stängt kan utbyta energi med miljön, men kan inte utbyta materia.
- Istället a isolerat system utbyter inte materia eller energi med miljön.
- Slutligen en öppna system utbyta materia och energi med miljön.
I reversibla processer beräknas variationen av intern energi enligt följande:
dU = TdS - PoV
Antag nu en process med konstant volym (isokorisk), där den andra termen i det föregående uttrycket inte har något bidrag. Det bör också komma ihåg att enligt Clausius ojämlikhet:
dS ≥ dQ / T
Sådan ojämlikhet gäller ett isolerat termodynamiskt system.
Så för en process (reversibel eller inte) där volymen förblir konstant, gäller följande:
T dS ≥ dU (vid fast volym)
Med hänsyn till att:
dF = dU - T dS
Vi kommer att ha att i en isokorisk process vid konstant temperatur är det nöjd med att: dF ≤ 0, som anges i början.
Så Helmholtz-energin F är en minskande kvantitet i en spontan process så länge det är ett isolerat system. F når sitt lägsta och stabila värde när reversibel jämvikt har uppnåtts.
Beräkna variationen av Helmholtz fria energi F för 2 mol idealgas vid en temperatur på 300K under en isotermisk expansion som tar systemet från en initial volym på 20 liter till en slutlig volym på 40 liter.
Från och med definitionen av F:
F = U - T S
Då kommer en ändlig variation av F, kallad ΔF, att vara:
ΔF = UU - T ΔS
Eftersom uttalandet säger att temperaturen är konstant: AT = 0. I ideala gaser beror nu den inre energin bara på deras absoluta temperatur, men eftersom det är en isotermisk process, då AU = 0 Y ΔF = - T ΔS. För ideala gaser skrivs entropiändringen av en isotermisk process så här:
AS = n.R.ln (V.två/ V1)
Tillämpar detta uttryck:
AS = 2 mol x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Slutligen är förändringen i Helmholtz-energin:
ΔF = - T ΔS = - 300 K x 11,53 J / K = -3457,70 J.
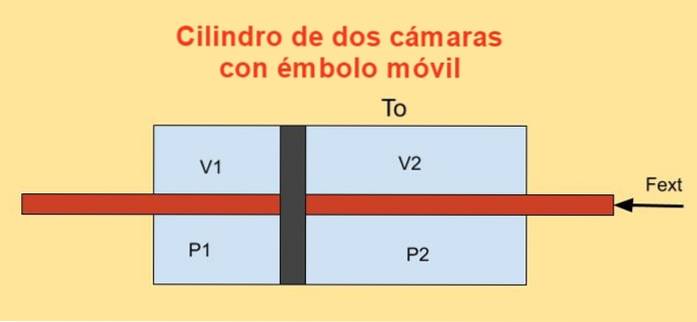
Inuti en cylinder finns en kolv som delar den i två sektioner och på varje sida av kolven finns det n mol av en monatomisk idealgas, som visas i figuren nedan.
Cylinderväggarna är goda värmeledare (diatermiska) och är i kontakt med en behållare med temperatur Teller.
Den initiala volymen för var och en av cylindersektionerna är V.1i och V2i, medan dess slutliga volymer är V1f och V2f efter kvasistatisk förskjutning. Kolven flyttas med hjälp av en kolv som hermetiskt passerar genom de två cylinderkåporna.
Det ombeds att hitta:
a) Förändringen av gasens inre energi och det arbete som utförs av systemet och
b) Variationen av Helmholtz-energin.
Eftersom kolven rör sig kvasistatiskt måste den yttre kraften som appliceras på kolven balansera kraften på grund av tryckskillnaden i cylinderns två sektioner..
Jobbet dW utförs av extern kraft Fext under ett oändligt minimalt skift dx det är:
dW = - Fext dx = (P1 - Ptvå) a dx = P1 dV1 + Ptvå dVtvå
Där förhållandet har använts dV1 = - dVtvå = a dx, varelse till kolvområdet. Å andra sidan är variationen i Helmholtz-energin:
dF = -SdT - PdV
Eftersom temperaturen inte ändras under processen, då dT = 0 Y dF = - PoV. Tillämpa detta uttryck på varje sektion av cylindern har vi:
dW = P1 dV1 + Ptvå dVtvå = - dF1 - dFtvå
Varelse F1 Y Ftvå Helmholtz-energierna i var och en av kamrarna.
Det ändliga arbetet W kan beräknas från den ändliga variationen av Helmholtz-energin i varje kammare:
W = -AF1 - AFtvå
För att hitta förändringen i Helmholtz-energin används definitionen: F = U - T S. Som i varje kammare finns en monatomisk idealgas vid konstant temperatur Teller, den inre energin förändras inte (ΔU = 0), så att: ΔF = - Teller AS. Vad mer:
AS = nR ln (V.F/Fick syn på)
Att när man ersätter till slut tillåter det arbete som utförts att vara:
W = -Teller nR ln (V1f / V1i) -Till nR ln (V.2f / V2i) = -AF1 -AFtvå
W = - Till nR ln [(V.1f ⋅ V1i) / (V2f .V2i)] = - AFtotal
Varelse AFtotal den totala förändringen i Helmholtz energi.
Ingen har kommenterat den här artikeln än.