
Termiska jämviktsekvationer, applikationer, övningar
Den termiska jämvikten för två kroppar som är i termisk kontakt är det tillstånd som nås efter en tillräckligt lång tid för att temperaturerna i båda kropparna ska utjämnas.
I termodynamik förstås termisk kontakt mellan två kroppar (eller två termodynamiska system) som en situation där kropparna har mekanisk kontakt eller är separerade men i kontakt med en yta som endast möjliggör passage av värme från en kropp till en annan yta).
-

Figur 1. Efter ett tag når isen och drycken sin termiska jämvikt. Källa: Pixabay
Vid termisk kontakt får det inte förekomma någon kemisk reaktion mellan systemen i kontakt. Det bör bara ske värmeväxling.
Vardagliga situationer där det sker värmeväxling sker med system som kall dryck och glas, varmt kaffe och tesked, eller kroppen och termometern, bland många andra exempel..
Artikelindex
- 1 När är två eller flera system i termisk jämvikt??
- 2 Ekvationer av termisk jämvikt
- 2.1 Jämviktstemperatur
- 2.2 Termisk kontakt med fasförändring
- 3 applikationer
- 3.1-Övning 1
- 4 Lösta övningar
- 4.1-Övning 2
- 4.2 Övning 3
- 4.3-Övning 4
- 5 Referenser
När två eller flera system är i termisk jämvikt?
Den andra lagen om termodynamik säger att värme alltid går från kroppen med den högsta temperaturen till kroppen med den lägsta temperaturen. Värmeöverföringen upphör så snart temperaturerna utjämnas och termisk jämvikt uppnås..
Den praktiska tillämpningen av termisk jämvikt är termometern. En termometer är en anordning som mäter sin egen temperatur, men tack vare termisk jämvikt kan vi känna till temperaturen hos andra kroppar, såsom den hos en person eller ett djur.
Kvicksilverkolonntermometern placeras i termisk kontakt med kroppen, till exempel under tungan, och tillräckligt med tid väntas för att den termiska jämvikten mellan kroppen och termometern ska uppnås och att dess avläsning inte varierar ytterligare.
När denna punkt har uppnåtts är temperaturen på termometern densamma som kroppens.
Termodynamikens nolllag säger att om en kropp A är i termisk jämvikt med en kropp C och att samma kropp C är i termisk jämvikt med B, så är A och B i termisk jämvikt även när det inte finns någon termisk kontakt mellan A och B.
Därför drar vi slutsatsen att två eller flera system är i termisk jämvikt när de har samma temperatur.
Termiska jämviktsekvationer
Vi antar en kropp A med initial temperatur Ta i termisk kontakt med en annan kropp B med initial temperatur Tb. Vi antar också att Ta> Tb, så överförs värmen från A till B enligt den andra lagen.
Efter ett tag uppnås termisk jämvikt och båda kropparna har samma slutliga temperatur Tf. Detta kommer att ha ett mellanvärde vid Ta och Tb, det vill säga Ta> Tf> Tb.
Mängden värme Qa som överförs från A till B kommer att vara Qa = Ma Ca (Tf-Ta), där Ma är massan av kropp A, Ca värmekapaciteten per enhetsmassa A och (Tf-Ta) temperaturskillnaden. Om Tf är mindre än Ta är Qa negativ, vilket indikerar att kroppen A ger upp värmen.
På samma sätt för kroppen B har vi att Qb = Mb Cb (Tf - Tb); och om Tf är större än Tb är Qb positivt, vilket indikerar att kropp B tar emot värme. Eftersom kropp A och kropp B är i termisk kontakt med varandra men isolerade från omgivningen måste den totala värmeväxlingen vara noll: Qa + Qb = 0
Sedan är Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Jämviktstemperatur
Att utveckla detta uttryck och lösa temperaturen Tf erhåller den slutliga temperaturen för termisk jämvikt.
-

Figur 2. Slutlig jämviktstemperatur. Källa: självtillverkad
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Tänk som fall på att kropparna A och B är identiska med avseende på massa och värmekapacitet, i detta fall är jämviktstemperaturen:
Tf = (Ta + Tb) / 2 ↔ om Ma = Mb och Ca = Cb.
Termisk kontakt med fasförändring
I vissa situationer händer det att när två kroppar placeras i termisk kontakt orsakar värmeväxlingen förändring av tillstånd eller fas i en av dem. Om detta händer måste man ta hänsyn till att det under fasförändringen inte sker någon temperaturförändring i kroppen som ändrar sitt tillstånd.
Om fasförändringen av någon av kropparna i termisk kontakt inträffar tillämpas begreppet latent värme L, vilket är den energi per massenhet som är nödvändig för tillståndsförändringen:
Q = L ∙ M
För att till exempel smälta 1 kg is vid 0 ° C krävs 333,5 kJ / kg och detta värde är latent värme L för smältning av is.
Under smältningen ändras det från fast vatten till flytande vatten, men det vattnet håller samma temperatur som is under smältprocessen..
Applikationer
Termisk balans är en del av det dagliga livet. Låt oss till exempel undersöka denna situation i detalj:
-Övning 1
En person vill bada i varmt vatten vid 25 ° C. Placera 3 liter kallt vatten i en hink vid 15 ° C och värm upp i 95 ° C i köket.
Hur många liter varmt vatten ska du lägga i hinken med kallt vatten för att få önskad slutstemperatur?
Lösning
Anta att A är kallt vatten och B är varmt vatten:
-
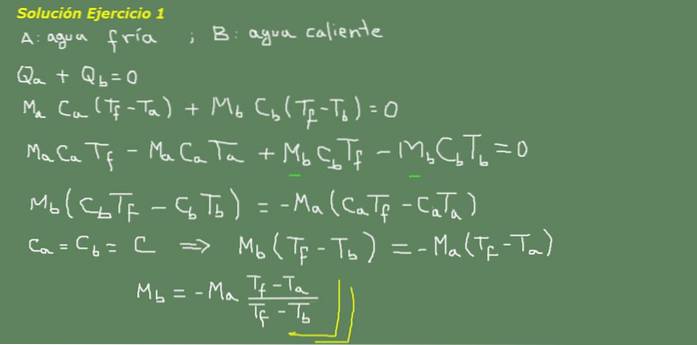
Figur 3. Lösning för övning 3. Källa: egen utarbetning.
Vi föreslår ekvationen av termisk jämvikt, som anges på tavlan i figur 3 och därifrån löser vi massan av vatten Mb.
Den initiala massan av kallt vatten kan erhållas eftersom vattnets densitet är känd, vilket är 1 kg per liter. Vi har 3 kg kallt vatten.
Ma = 3 kg
Sedan
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Då räcker det med 0,43 liter varmt vatten för att slutligen få 3,43 liter varmt vatten vid 25 ° C.
Lösta övningar
-Övning 2
En metallbit med en massa av 150 g och en temperatur på 95 ° C införs i en behållare som innehåller en halv liter vatten vid en temperatur av 18 ° C. Efter ett tag uppnås den termiska jämvikten och temperaturen på vattnet och metallen är 25 ° C.
Antag att behållaren med vattnet och metallbiten är en sluten termos som inte tillåter värmeväxling med miljön.
Skaffa metallens specifika värme.
Lösning
Först beräknar vi värmen som absorberas av vattnet:
Qa = Ma Ca (Tf - Ta)
Qa = 500g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 kalorier.
Det är samma värme som metallen ger:
Qm = 150 g Cm (25 ° C - 95 ° C) = -3500 kalorier.
Så vi kan få metallens värmekapacitet:
Cm = 3500 cal / (150g 70 ° C) = ⅓ cal / (g ° C).
Övning 3
Du har 250 c.c. vatten vid 30 ° C. Till det vattnet som är i en isolerande termos tillsätts 25 g isbitar vid 0 ° C i syfte att kyla det.
Bestäm jämviktstemperaturen; det vill säga temperaturen som kommer att förbli när all isen har smält och isvattnet har värmts upp för att matcha temperaturen i vattnet i glaset från början.
Lösning 3
Denna övning kan lösas i tre steg:
- Den första är issmältningen som absorberar värme från det ursprungliga vattnet för att smälta och bli vatten..
- Sedan beräknas temperaturfallet i det ursprungliga vattnet på grund av att det har gett upp värme (Qced<0) para fundir el hielo.
- Slutligen måste det smälta vattnet (som kommer från isen) balanseras termiskt med det vatten som fanns ursprungligen..
-

Figur 4. Lösning för övning 3. Källa: egen utarbetning.
Låt oss beräkna den värme som krävs för att smälta is:
Qf = L * Mh = 333,5 kJ / kg * 0,025 kg = 8,338 kJ
Därefter är värmen som vattnet ger för att smälta isen Qced = -Qf
Denna värme som avges av vattnet sänker temperaturen till ett värde T 'som vi kan beräkna enligt följande:
T '= T0 - Qf / (Ma * Ca) = 22,02 ° C
Där Ca är vattenets värmekapacitet: 4,18 kJ / (kg ° C).
Slutligen kommer den ursprungliga massan av vatten som nu är 22.02 ° C att ge upp värmen till massan av smält vatten från isen som ligger vid 0 ° C..
Slutligen uppnås jämviktstemperaturen Te efter tillräcklig tid:
Te = (Ma * T '+ Mh * 0 ° C) / (Ma + Mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).
Slutligen erhåller jämviktstemperaturen:
Te = 20,02 ° C.
-Övning 4
En 0,5 kg bit bly kommer ut ur ugnen vid en temperatur av 150 ° C, vilket ligger långt under smältpunkten. Denna bit placeras i en behållare med 3 liter vatten vid rumstemperatur på 20 ° C. Bestäm den slutliga jämviktstemperaturen.
Beräkna också:
- Mängden värme som levereras av bly till vatten.
- Mängden värme som absorberas av vatten.
Data:
Specifik blyvärme: Cp = 0,03 cal / (g ° C); specifik vattenvärme: Ca = 1 cal / (g ° C).
Lösning
Först bestämmer vi den slutliga jämviktstemperaturen Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C
Då är mängden värme som frigörs av bly:
Qp = Mp Cp (Te - Tp) = -1,94 x 10 ^ kal.
Mängden värme som absorberas av vattnet kommer att vara:
Qa = Ma Ca (Te - Ta) = + 1,94x 10³ kal.
Referenser
- Atkins, P. 1999. Fysisk kemi. Omega-utgåvor.
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e ... Ed Prentice Hall.
- Hewitt, Paul. 2012. Konceptuell fysik. 5: e. Ed Pearson.
- Resnick, R. (1999). Fysisk. Vol. 1. 3: e upplagan på spanska. Compañía Editorial Continental S.A. av C.V.
- Rex, A. 2011. Grundläggande fysik. Pearson.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Utg. Volym 1.
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7: e. Ed. Cengage Learning.



Ingen har kommenterat den här artikeln än.