Elektriskt fältflöde

Vad är elektriskt fältflöde?

De elektrisk fältflöde eller helt enkelt elflöde är en skalär kvantitet som är proportionell mot antalet elektriska fältlinjer som passerar genom en yta. Det betecknas med den grekiska bokstaven Φ (phi).

Det elektriska fältet "strömmar" faktiskt inte på det sätt som en ström av vatten gör, även om strömningslinjerna för vätskan liknar de i det elektriska fältet..

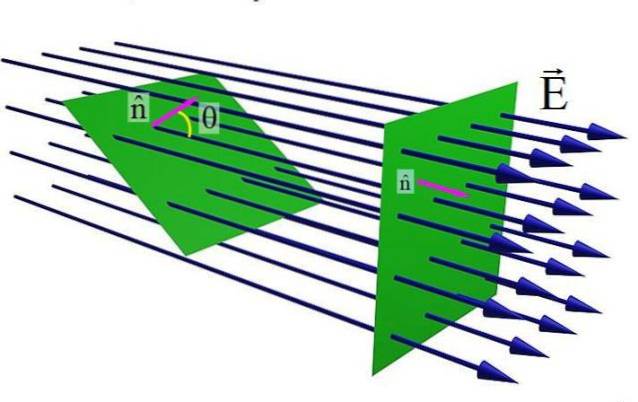
Bilden ovan visar en plan yta som korsas av ett elektriskt fält OCH. När enhetsvektorn är normal mot ytan n och fältet OCH är parallella, är antalet fältlinjer som passerar ytan maximalt. Men som vinkeln θ mellan n Y OCH, antalet linjer som passerar genom den gröna ytan är mindre.

Å andra sidan beror det elektriska fältflödet också på storleken på OCH, för ju större detta desto fler fältlinjer korsar ytan. Och naturligtvis, ju större yta S på ytan är, desto större är flödet, så följande ekvation upprättas:

Φ = E ∙ Scosθ

Detta uttryck överensstämmer med punktprodukten mellan vektorerna OCH Y n:

Φ = (OCH • n) S

Enheten för elektriskt fältflöde i SI International System of Units är N.m^två/ C (newton x kvadratmeter / coulomb). Alternativt, eftersom fältet också mäts i V / m (volt över meter), förblir det elektriska flödet i (V ∙ m).

Exempel

Enligt definitionen kan det elektriska flödet vara positivt, negativt eller lika med 0. Det elektriska fältflödet är:

-Positiv när vinkel θ mellan OCH Y n är mindre än 90 °, eftersom cos θ är större än noll.

-Negativt om nämnda vinkel är större än 90 °, för då är cos θ mindre än noll.

-Noll när θ är exakt 90º, eftersom cos 90º = 0 och fältlinjerna i detta fall är tangentiella mot ytan.

-Å andra sidan, om vinkeln mellan OCH Y n är lika med 0, får flödet sitt maximala värde.

Dessa möjligheter visas i följande bild:

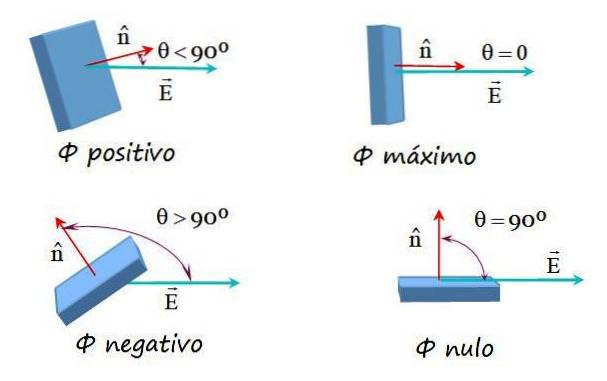
Elektriskt fältflöde på en godtycklig yta

Tidigare bestämdes det elektriska fältflödet i det speciella fallet av ett enhetligt fält som inträffar på en plan yta. För en yta med godtycklig form S och / eller ett ojämnt elektriskt fält, vinkeln mellan OCH Y n kan variera från punkt till punkt.

I följande figur finns två exempel, till vänster en krökt yta och till höger en sluten yta.

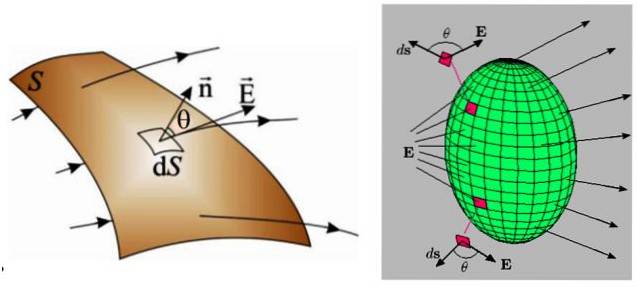
I båda fallen är ytan uppdelad i mycket mindre regioner, av oändlig storlek, kallad dS, genom vilken ett flöde också oändligt stort dΦ passerar genom:

dΦ = (OCH•n) dS = (Ecos2) dS

Det totala fältet erhålls genom att lägga till alla dessa oändliga bidrag:

Vid stängda ytor, n pekar alltid utåt, därför har flödet ett + -tecken när det är framträdande för S, eftersom vinkeln mellan OCH Y n är mindre än 90º, och underteckna - när fältet är inkommande, för då är vinkeln mellan OCH Y n är större än 90º (se figur 2).

Observera att i den stängda ytan till höger är antalet fältlinjer som kommer in i ytan lika med antalet linjer som lämnar. Därför är nätflödet, definierat som den algebraiska summan av det inkommande flödet och det utgående flödet, noll.

Källan till det elektriska fältet ligger i detta fall utanför ytan, men nätflödet skulle skilja sig från 0 om källan till det elektriska fältet (fördelningen av laddningar) var inne i ytan..

Träning

Övning 1

Det har ett elektriskt fält OCH = 3,5 kN / C x och en plan rektangulär yta 0,35 m bred och 0,7 m lång. Hitta det elektriska fältflödet genom rektangeln i följande fall:

a) Ytan är parallell med yz-planet.

b) Rektangeln är parallell med xy-planet.

c) Planets normala bildar en vinkel på 40º med x-axeln och innehåller y-axeln.

Lösning till

Den normala vektorn och den elektriska fältvektorn är parallella, därför är vinkeln θ mellan dem 0º och det elektriska flödet är:

Φ = (E ∙ S) cos 0 = E ∙ S

Rektangelns område S är:

S = 0,35 m x 0,7 m = 0,245 m^två

Ersätter i Φ:

Φ = E ∙ S = 3,5 x 10³ N / C × 0,245 m^två = 857,5 N ∙ m^två / C.

Lösning b

Det elektriska fältflödet är 0, eftersom vektorerna OCH Y n är vinkelräta mot varandra.

Lösning c

Vinkeln θ mellan fältet OCH och den normala vektorn n är 40º (se figur), därför:

Φ = E ∙ S ∙ cos θ = 3,5 x 10³ N / C × 0,245 m^två × cos 40º = 656,9 N ∙ m^två / C.

Övning 2

Beräkna det elektriska fältflödet som producerar en positiv punktladdning q_eller = 2μC i mitten av en sfär med radie R = 5 cm.

Lösning

Fältet som produceras av laddningen q_eller Det är inte enhetligt, men från Coulombs lag är det känt att det på sfärens yta har en storlek på:

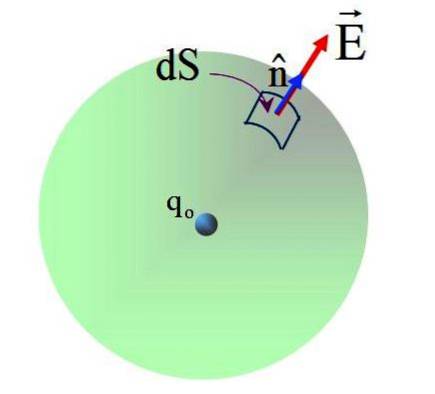
Fältet har en radiell riktning och den normala vektorn n, därför är vinkeln mellan båda vektorerna 0 vid varje punkt på den sfäriska ytan. Ersätter i:

Det måste:

Integralen av dS över hela sfäriska ytan S är dess area, vilket är 4πR^två, Således:

Dess värde är:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m^två/ C = 2,3 x 10⁵ N⋅m^två/ C

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
2. Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 5. Elektrostatik. Redigerad av Douglas Figueroa (USB).
3. Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
4. Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Red. Volym 1. Pearson.