
Absolut frekvensformel, beräkning, fördelning, exempel
De Absolut frecuency Det definieras som antalet gånger som samma data upprepas inom uppsättningen observationer av en numerisk variabel. Summan av alla absoluta frekvenser motsvarar sammanlagda data.
När du har många värden på en statistisk variabel är det bekvämt att ordna dem på lämpligt sätt för att extrahera information om dess beteende. Sådan information ges av måtten på den centrala tendensen och måtten på spridning..
I beräkningarna av dessa mått representeras data genom frekvensen med vilken de visas i alla observationer..
Följande exempel visar hur avslöjar den absoluta frekvensen för varje datadel. Under första halvan av maj var det de bästsäljande cocktailklänningsstorlekarna från en välkänd damklädaffär:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Hur många klänningar säljs i en viss storlek, till exempel storlek 10? Ägare är intresserade av att veta att beställa.
Att beställa data gör det lättare att räkna, det finns exakt 30 observationer totalt, som beställts från den minsta till den största är följande:
4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18
Och nu är det uppenbart att storlek 10 upprepas 6 gånger, därför är dess absoluta frekvens lika med 6. Samma procedur utförs för att ta reda på den absoluta frekvensen för de återstående storlekarna..
Artikelindex
- 1 Formler
- 1.1 Övriga frekvenser
- 2 Hur man får den absoluta frekvensen?
- 2.1 Tabell
- 2.2 Utökad frekvenstabell
- 3 Frekvensfördelning
- 3.1 Frekvensfördelning för grupperade data
- 4 Exempel
- 5 Övningen löst
- 5.1 Lösning
- 6 Referenser
Formler
Den absoluta frekvensen, betecknad som fi, är lika med antalet gånger som ett visst värde Xi är inom gruppen observationer.
Om vi antar att den totala observationen är N-värden, måste summan av alla absoluta frekvenser vara lika med detta tal:
∑fi = f1 + Ftvå + F3 +... fn = N
Andra frekvenser
Om varje värde av fi dividerat med det totala antalet data N, har vi relativ frekvens Fr av X-värdeti:
Fr = fi / N
Relativa frekvenser är värden mellan 0 och 1, eftersom N alltid är större än någon fi, men summan måste vara lika med 1.
Multiplicera varje värde av f med 100r du har procentuell relativ frekvens, vars summa är 100%:
Procentuell relativ frekvens = (fi / N) x 100%
Det är också viktigt kumulativa frekvensen Fi upp till en viss observation är detta summan av alla absoluta frekvenser till och med nämnda observation:
Fi = f1 + Ftvå + F3 +... fi
Om den ackumulerade frekvensen divideras med det totala antalet data N, har vi kumulativ relativ frekvens, som multipliceras med 100 ger procentuell kumulativ relativ frekvens.
Hur får man den absoluta frekvensen?
För att hitta den absoluta frekvensen för ett visst värde som tillhör en datamängd, är alla organiserade från lägsta till högsta och antalet gånger värdet visas räknas.
I exemplet med klädstorlekar är den absoluta frekvensen för storlek 4 tre klänningar, det vill säga f1 = 3. För storlek 6 såldes 4 klänningar: ftvå = 4. I storlek 8 såldes också 4 klänningar, f3 = 4 och så vidare.
Tabulering
De totala resultaten kan representeras i en tabell som visar de absoluta frekvenserna för var och en:
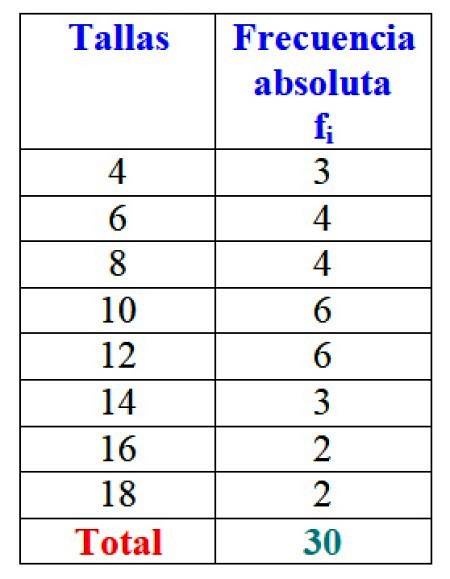
Uppenbarligen är det fördelaktigt att organisera informationen och kunna komma åt den med en överblick, istället för att arbeta med enskilda data.
Viktig: notera att när du lägger till alla värden i kolumn fi du får alltid det totala antalet data. Om inte, måste du kontrollera bokföringen, eftersom det finns ett fel.
Utökad frekvenstabell
Ovanstående tabell kan utökas genom att lägga till andra frekvenstyper i på varandra följande kolumner till höger:
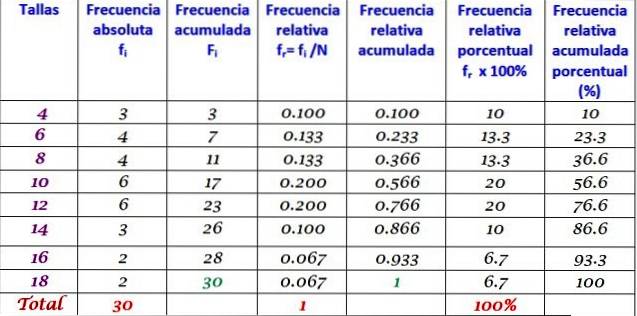
Frekvensfördelning
Frekvensfördelningen är resultatet av att organisera data i termer av deras frekvenser. När du arbetar med många data är det bekvämt att gruppera dem i kategorier, intervall eller klasser, var och en med sina respektive frekvenser: absolut, relativ, ackumulerad och procent..
Målet med att göra dem är att lättare få tillgång till informationen i uppgifterna, samt att tolka dem ordentligt, vilket inte är möjligt när de presenteras i ingen ordning..
I exemplet med storlekar grupperas inte data eftersom de inte är för många storlekar och kan enkelt manipuleras och redovisas. Kvalitativa variabler kan också bearbetas på detta sätt, men när data är mycket många är det bättre att arbeta genom att gruppera dem i klasser.
Frekvensfördelning för grupperade data
För att gruppera dina data i klasser av samma storlek, överväg följande:
-Klassstorlek, bredd eller bredd: är skillnaden mellan det högsta värdet i klassen och det lägsta.
Klassens storlek bestäms genom att dividera rang R med antalet klasser som ska beaktas. Området är skillnaden mellan det maximala värdet på data och det minsta, så här:
Klassstorlek = Rank / antal klasser.
-Klassgräns: intervall från den nedre gränsen till klassens övre gräns.
-Klassmärke: är mittpunkten för intervallet, vilket anses vara representativt för klassen. Den beräknas med halvsumman av den övre gränsen och klassens nedre gräns.
-Antal klasser: Sturges-formel kan användas:
Antal klasser = 1 + 3 322 log N
Där N är antalet klasser. Eftersom det vanligtvis är ett decimaltal avrundas det till nästa heltal.
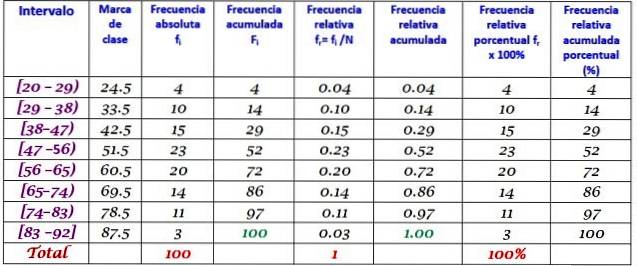
Exempel
En maskin i en stor fabrik är ur drift på grund av återkommande fel. De på varandra följande perioderna av inaktivitet i minuter, för nämnda maskin, registreras nedan, med totalt 100 data:
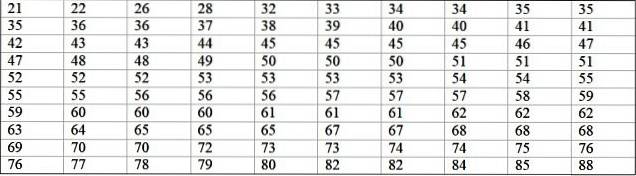
Först bestäms antalet klasser:
Antal klasser = 1 + 3 322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Klassstorlek = Område / Antal klasser = (88-21) / 8 = 8,375
Det är också ett decimaltal, så 9 tas som klassstorlek.
Klassmärket är medelvärdet mellan klassens övre och nedre gräns, till exempel för klass [20-29] finns det ett märke på:
Klassmärke = (29 + 20) / 2 = 24,5
Vi fortsätter på samma sätt för att hitta klassmärken för återstående intervall.
Övningen löst
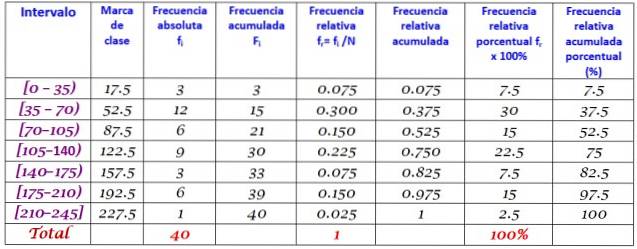
40 ungdomar indikerade att tiden i minuter de tillbringade på internet förra söndagen var följande, ordnad i ökande ordning:
0; 12; tjugo; 35; 35; 38; 40; Fyra fem; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Det uppmanas att konstruera frekvensfördelningen för dessa data.
Lösning
Området R för uppsättningen N = 40 data är:
R = 220 - 0 = 220
Att använda Sturges-formeln för att bestämma antalet klasser ger följande resultat:
Antal klasser = 1 + 3 322 log N = 1 + 3,32 log 40 = 6,3
Eftersom det är ett decimal är det omedelbara heltalet 7, därför grupperas data i 7 klasser. Varje klass har en bredd på:
Klassstorlek = Rang / Antal klasser = 220/7 = 31.4
Ett nära och runt värde är 35, därför väljs en klassbredd på 35.
Klassmärken beräknas genom medelvärdet av de övre och nedre gränserna för varje intervall, till exempel för intervallet [0,35):
Klassmärke = (0 + 35) / 2 = 17,5
Fortsätt på samma sätt som de andra klasserna.
Slutligen beräknas frekvenserna enligt proceduren som beskrivs ovan, vilket resulterar i följande fördelning:
Referenser
- Berenson, M. 1985. Statistik för management och ekonomi. Interamericana S.A.
- Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
- Levin, R. 1988. Statistik för administratörer. 2: a. Utgåva. Prentice hall.
- Spiegel, M. 2009. Statistik. Schaum-serien. 4: e Utgåva. Mcgraw hill.
- Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.


Ingen har kommenterat den här artikeln än.