
Statisk friktionskoefficient, exempelvis träning

De statisk friktion är den kraft som uppstår mellan två ytor när en yta inte glider i förhållande till den andra. Det är mycket viktigt, eftersom det gör att vi kan gå framåt när vi går, eftersom det är kraften som finns mellan golvet och skosulan.
Det är också statisk friktion som uppträder mellan trottoaren och bilens däck. Om denna kraft inte är närvarande är det omöjligt för bilen att börja röra sig, som det händer i en bil som försöker starta på en isig yta: hjulen glider men bilen rör sig inte.

Statisk friktion beror på ytornas grovhet i kontakt och även på vilken typ av material de är tillverkade av. Det är därför däcken och sportskorna är gjorda av gummi för att öka friktionen med trottoaren..
I den statiska friktionsmodellen sammanfattas materialets egenskaper och grovhetsgraden mellan ytorna i ett nummer som kallas statisk friktionskoefficient, som bestäms experimentellt.
Artikelindex
- 1 Koefficient för statisk friktion
- 2 Exempel: bestämning av den statiska friktionskoefficienten
- 3 Träning
- 3.1 Lösning
- 4 Referenser
Statisk friktionskoefficient

Bilden ovan visar en bok som ligger på ett bord med en lutning på 15,7º.
Om ytorna på boken och bordet var mycket släta och polerade kunde inte boken stå stilla. Men eftersom de inte är det, verkar en kraft som är tangent till ytorna i kontakt som kallas kraften för statisk friktion.
Om lutningsvinkeln är tillräckligt stor är det inte tillräckligt statisk friktionskraft för att balansera boken och den skulle börja glida.
I det här fallet finns det också friktion mellan boken och bordet, men det skulle vara en styrka av dynamisk friktion, även kallad kinetisk friktion.
Det finns en gräns mellan statisk friktion och dynamisk friktion, som inträffar när den statiska friktionen når sitt maximala värde.
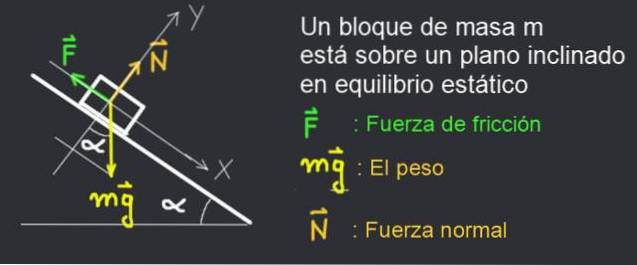
Låt oss överväga i figur 2 kraftdiagrammet för en massbok m som hålls i vila på ett lutningsplan α.
Boken ligger i vila eftersom den statiska friktionskraften F balanserar systemet.
Om lutningsvinkeln ökar lite måste ytorna i kontakt ge mer friktionskraft, men mängden statisk friktion som ytorna i kontakt kan ge har en maximal gräns Fmax, nämligen:
F ≤ Fmax.
Den maximala statiska friktionskraften beror på materialen och graden av ytor som är i kontakt samt greppets fasthet.
Den statiska friktionskoefficienten μoch är ett positivt tal som beror på egenskaperna hos ytorna i kontakt. Normal styrka N som planet utövar på blocket visar graden av täthet mellan blockets yta och planet. Så här bestämmer de den maximala friktionskraften som ytorna ger när det inte glider:
Fmax = μoch N
Sammanfattningsvis följer den statiska friktionskraften följande modell:
F ≤ μoch N
Exempel: bestämning av den statiska friktionskoefficienten
Den statiska friktionskoefficienten är ett dimensionslöst tal som bestäms experimentellt för varje yta.
Vi betraktar blocket i vila i figur 2. Följande krafter verkar på det:
- Friktionskraft: F
- Vikten av massblocket m: mg
- Normal styrka: N
Eftersom blocket är i vila och inte har någon acceleration, enligt Newtons andra lag, är den resulterande kraften - en vektorsumma - noll:
F + N + mg = 0
Ett fast XY-koordinatsystem betraktas med X-axeln längs det lutande planet och Y-axeln vinkelrätt mot det, såsom visas i figur 2.
Krafterna måste separeras enligt deras kartesiska komponenter, vilket ger upphov till följande ekvationssystem:
-Komponent X: -F + mg Sen (a) = 0
-Komponent Y: N - mg Cos (a) = 0
Värdet på den statiska friktionskraften löses från den första ekvationen:
F = mg Sen (a)
Och från det andra värdet av den normala kraften:
N = mg Cos (a)
Den statiska friktionskraften F följer följande modell:
F ≤ μoch N
Att ersätta de tidigare erhållna värdena i den ojämlikhet vi har:
mg Sen (α) ≤ μoch mg Cos (a)
Med tanke på att för värdena α mellan 0º och 90º, är sinus- och cosinusfunktionerna båda positiva, och att kvoten mellan sinus och cosinus är tangenten, har vi:
Tan (α) ≤ μoch
Jämställdheten gäller för ett visst värde av α kallad kritisk vinkel och som vi betecknar med α *, det vill säga:
μoch = Solbränd (α *)
Den kritiska vinkeln bestäms experimentellt, gradvis ökar lutningen tills den rätta vinkeln vid vilken blocket börjar glida, det vill säga den kritiska vinkeln α *.
I boken i figur 1 bestämdes denna vinkel experimentellt vilket resulterade i 24 °. Då är koefficienten för statisk friktion:
μoch = Solbränd (24º) = 0,45.
Det är ett positivt tal mellan 0 och oändlighet. Om μoch = 0 ytorna är helt släta. Om μoch → ∞ ytorna är perfekt fogade eller svetsade.
I allmänhet är värdet på friktionskoefficienten mellan 0 och 10.
Övning
I sprint- eller dragsterlopp uppnås accelerationer på upp till 4 g under start, vilket uppnås exakt när däcken inte glider i förhållande till trottoaren..
Detta beror på att den statiska friktionskoefficienten alltid är större än den dynamiska friktionskoefficienten..
Förutsatt att fordonets totala vikt plus föraren är 600 kg och att bakhjulen uppbär 80% av vikten bestämmer du den statiska friktionskraften under 4g-start och koefficienten för statisk friktion mellan däcken och trottoaren..

Lösning
Enligt Newtons andra lag är den resulterande kraften lika med den totala massan av fordonet gånger den acceleration som den får.
Eftersom fordonet befinner sig i vertikal jämvikt avbryts det normala och vikten, vilket resulterar i att friktionskraften F som trottoaren utövar på drivhjulens kontaktyta lämnas och lämnar:
F = m (4g) = 600 kg (4 x 9,8 m / stvå) = 23520 N = 2400 kg-f
Detta innebär att dragkraften är 2,4 ton.
Friktionskraften som hjulet utövar på marken går bakåt, men dess reaktion, som är densamma och motsatt, verkar på däcket och går framåt. Det är den kraft som driver fordonet.
Naturligtvis produceras all denna kraft av motorn som försöker skjuta tillbaka golvet genom hjulet, men hjulet och golvet är kopplade av friktionskraft.
För att bestämma koefficienten för statisk friktion använder vi det faktum att den erhållna F är den maximala möjliga friktionen, eftersom vi är vid gränsen för maximal acceleration, därför:
F = μoch N = μe (0,8 mg)
Det faktum att de bakre drivhjulen stöder 0,8 gånger vikten togs med i beräkningen. Lösning av friktionskoefficienten får vi:
μoch = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Slutsats: μoch = 5.
Referenser
- Alonso M., Finn E. 1970. Fysikvolym I: Mekanik. Interamerikansk utbildningsfond S.A.
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Hewitt, P. 2012. Konceptuell fysik. Femte upplagan.
- Rex, A. 2011. Grundläggande fysik. Pearson. 190-200.
- Young, Hugh. 2015. Universitetsfysik med modern fysik. 14: e utgåvan Pearson.



Ingen har kommenterat den här artikeln än.