
Bijektiv funktion vad är det, hur görs det, exempel, övningar

A bijektiv funktion är en som uppfyller det dubbla villkoret att vara injektiv och surjektiv. Det vill säga att alla element i domänen har en enda bild i kodmenyn, och i sin tur är kododen lika med funktionens rang ( RF ).
Det uppfylls genom att överväga ett en-till-ett-förhållande mellan elementen i domänen och kodmän. Ett enkelt exempel är funktionen F: R → R definieras av linjen F (x) = x
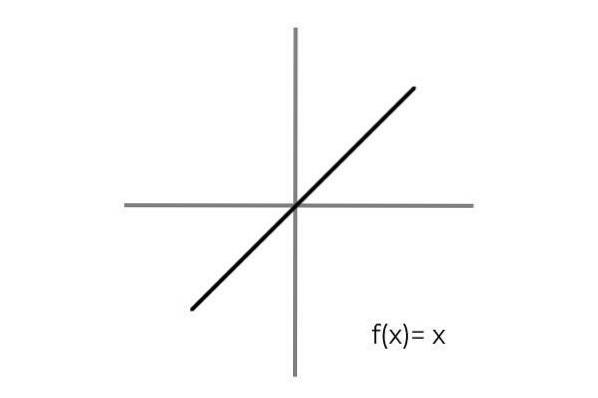
Det observeras att för varje värde på domänen eller startuppsättningen (båda termerna gäller lika) finns det en enda bild i kod- eller ankomstuppsättningen. Dessutom finns det inget element i kodmenyn som inte är en bild.
Således F: R → R definieras av linjen F (x) = x är bindande
Artikelindex
- 1 Hur gör du en bijektiv funktion?
- 1.1 Injektivitet av en funktion
- 1.2 Surjektivitet för en funktion
- 1.3 Funktionskonditionering
- 2 Exempel: lösta övningar
- 2.1 Övning 1
- 2.2 Övning 2
- 2.3 Övning 3
- 2.4 Övning 4
- 3 Föreslagna övningar
- 4 Referenser
Hur gör du en bijektiv funktion?
För att svara på detta är det nödvändigt att vara tydlig om begreppen som hänvisar till Injektivitet Y Surjektivitet för en funktion, utöver kriterierna för att konditionera funktioner för att anpassa dem till kraven.
Injektivitet av en funktion
En funktion är injektionsvätska när vart och ett av elementen i dess domän är relaterat till ett enda element i kodmenyn. Ett element i codomain kan bara vara bilden av ett enda element i domänen, på detta sätt kan värdena för den beroende variabeln inte upprepas.
Att överväga injektionsvätska till en funktion måste följande uppfyllas:
∀ x1 ≠ xtvå ⇒ F (x1 ) ≠ F (xtvå )
Surjektivitet för en funktion
En funktion klassificeras som förväntningar, om varje element i dess kodomän är en bild av minst ett element i domänen.
Att överväga förväntningar till en funktion måste följande uppfyllas:
Vara F: DF → CF
∀ b ℮ CF OCH till ℮ DF / F (a) = b
Detta är det algebraiska sättet att fastställa att för varje "b" som tillhör CF det finns ett “a” som tillhör DF så att funktionen utvärderad i "a" är lika med "b".
Funktionskonditionering
Ibland en funktion som inte är det bijective, det kan utsättas för vissa villkor. Dessa nya villkor kan göra det till en bijektiv funktion. Alla typer av modifieringar av funktionens domän och kodnamn är giltiga, där målet är att uppfylla egenskaperna för injektivitet och överföringsförmåga i motsvarande relation..
Exempel: övningar lösta
Övning 1
Låt funktionen F: R → R definieras av linjen F (x) = 5x +1
A: [Alla verkliga siffror]
Det observeras att för varje värde av domänen finns en bild i kodmenyn. Denna bild är unik vilket gör F vara en injektionsfunktion. På samma sätt observerar vi att kodens huvudfunktion är lika med dess rang. Således uppfyller villkoret för surjectivity.
Att vara injektiv och surjektiv samtidigt kan vi dra slutsatsen att
F: R → R definieras av linjen F (x) = 5x +1 är en bijektiv funktion.
Detta gäller för alla linjära funktioner (funktioner vars största variabel är en).
Övning 2
Låt funktionen F: R → R definieras av F (x) = 3xtvå - två
När man drar en horisontell linje observeras att grafen hittas vid mer än ett tillfälle. På grund av detta funktionen F det är inte injektivt och kommer därför inte att vara det bijective så länge det är definierat i R → R
På samma sätt finns kodvärdenas värden som inte är bilder av något element i domänen. På grund av detta är funktionen inte förväntad, vilket också förtjänar att villkora ankomstuppsättningen.
Vi fortsätter med att konditionera funktionens domän och codomain
F: [0 , ∞] → [- två , ∞ ]
Där det observeras att den nya domänen omfattar värdena från noll till positiv oändlighet. Undvik upprepning av värden som påverkar injektionsförmågan.
Likaså har kodmoden modifierats, räknat från "-2" till positiv oändlighet, vilket eliminerar från kodomän de värden som inte motsvarade något element i domänen
På detta sätt kan det säkerställas att F : [0 , ∞] → [- två , ∞ ] definieras av F (x) = 3xtvå - två
Det är bindande
Övning 3
Låt funktionen F: R → R definieras av F (x) = Sen (x)
I intervallet [ -∞ , +∞ ] sinusfunktionen varierar sina resultat mellan noll och en.
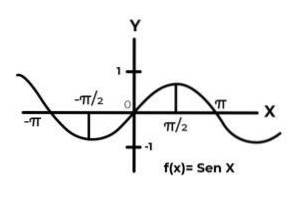
Funktionen F det motsvarar inte kriterierna för injektivitet och surjektivitet, eftersom värdena för den beroende variabeln upprepas varje intervall av π. Också villkoren för codomain utanför intervallet [-elven] De är inte en bild av något element i domänen.
När du studerar grafen för funktionen F (x) = Sen (x) intervaller observeras där kurvens beteende uppfyller kriterierna för bijektivitet. Som till exempel intervallet DF = [ π / 2,3π / 2 ] för domänen. Y CF = [-1, 1] för codomain.
Där funktionen varierar från 1 till -1, utan att upprepa något värde i den beroende variabeln. Och samtidigt är codomain lika med de värden som antagits av uttrycket Sen (x)
På detta sätt funktionen F: [ π / 2,3π / 2 ] → [-1, 1] definieras av F (x) = Sen (x). Det är bindande
Övning 4
Ange nödvändiga villkor för DF och CF. Så uttrycket
F (x) = -xtvå vara bijective.
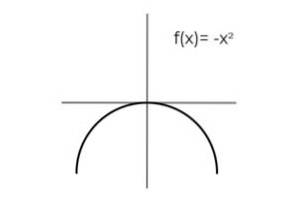
Upprepningen av resultaten observeras när variabeln tar motsatta värden:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
Domänen är konditionerad och begränsar den till höger om den verkliga linjen.
DF = [0 , +∞ ]
På samma sätt observeras att intervallet för denna funktion är intervallet [ -∞ , 0], som när de fungerar som en koddom uppfyller villkoren för surjektivitet.
På detta sätt kan vi dra slutsatsen att
Uttrycket F: [0 , +∞ ] → [ -∞ , 0] definieras av F (x) = -xtvå Det är bindande
Föreslagna övningar
Kontrollera om följande funktioner är kompatibla:
F: [0 , ∞) → R definieras av F (x) = 3 (x + 1)två +två
F: [ 3π / 2,5π / 2 ] → R definieras av F (x) = 5ctg (x)
F: [ -π,π ] → R definieras av F (x) = Cos (x - 3)
F: R → R definieras av linjen F (x) = -5x + 4
Referenser
- Introduktion till logik och kritiskt tänkande. Merrilee H. lax. University of Pittsburgh
- Problem i matematisk analys. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polen.
- Element av abstrakt analys. Mícheál O'Searcoid PhD. Institutionen för matematik. University College Dublin, Beldfield, Dublind 4
- Introduktion till logik och metoderna för deduktiva vetenskaper. Alfred Tarski, Oxford i New York. Oxford University press.
- Principer för matematisk analys. Enrique Linés Escardó. Ledare Reverté S. A 1991. Barcelona Spanien.



Ingen har kommenterat den här artikeln än.