
Hypercube-definition, dimensioner, koordinater, utbrett
A hypercube är en kub med dimension n. Det speciella fallet med den fyrdimensionella hyperkuben kallas tesseract. En hyperkub eller n-kub består av raka segment, alla lika långa som är ortogonala vid sina hörn.
Människor uppfattar tredimensionellt utrymme: bredd, höjd och djup, men det är inte möjligt för oss att visualisera en hyperkub med en dimension större än 3.
Högst kan vi göra projektioner av det i tredimensionellt utrymme för att representera det, på ett liknande sätt som hur vi projicerar en kub i ett plan för att representera den..
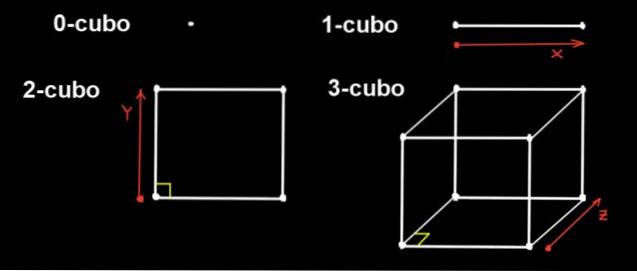
I dimension 0 är den enda figuren punkten, så en 0-kub är en punkt. En 1-kub är ett rakt segment som bildas genom att flytta en punkt i en riktning ett avstånd a.
För sin del är en 2-kub en kvadrat. Den är konstruerad genom att förskjuta 1-kuben (segmentet längd a) i y-riktningen, som är ortogonal mot x-riktningen, ett avstånd a.
3-kuben är den vanliga kuben. Den byggs från torget genom att flytta den i den tredje riktningen (z), som är ortogonal mot x- och y-riktningarna, ett avstånd till.
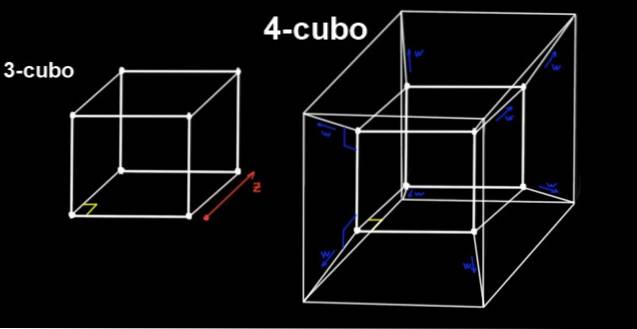
4-kuben är tesserakt, som är byggd av en 3-kub som förskjuter den ortogonalt, ett avstånd till, mot en fjärde dimension (eller fjärde riktning), som vi inte kan uppfatta.
En tesserakt har alla sina räta vinklar, den har 16 hörn, och alla dess kanter (18 totalt) har samma längd till.
Om längden på kanterna på en n-kub eller hyperkub med dimensionen n är 1, är det en enhetshyperkub, där den längsta diagonalen mäter √n.

Artikelindex
- 1 Vad är dimensioner??
- 1.1 Det tredimensionella utrymmet
- 2 Koordinaterna för en hyperkub
- 2.1 Vik upp en hyperkub
- 3 Referenser
Vad är dimensioner?
Mått är frihetsgraderna eller de möjliga riktningar som ett objekt kan röra sig i.
I dimension 0 finns ingen möjlighet att översätta och det enda möjliga geometriska objektet är punkten.
En dimension i det euklidiska utrymmet representeras av en orienterad linje eller axel som definierar den dimensionen, kallad X-axeln. Avståndet mellan två punkter A och B är det euklidiska avståndet:
d = √ [(xtill - xb)två].
I två dimensioner representeras rymden av två linjer orienterade ortogonala mot varandra, kallade X-axeln och Y-axeln..
Positionen för vilken punkt som helst i detta tvådimensionella utrymme ges av dess par kartesiska koordinater (x, y) och avståndet mellan två punkter A och B kommer att vara:
d = √ [(xtill - xb)två + (Ytill - Yb)två]
Eftersom det är ett utrymme där Euklids geometri uppfylls.
Tredimensionellt utrymme
Tredimensionellt utrymme är det utrymme vi rör oss i. Den har tre riktningar: bredd, höjd och djup.
I ett tomt rum ger hörnen vinkelrätt mot varandra dessa tre riktningar och till var och en kan vi associera en axel: X, Y, Z.
Detta utrymme är också euklidiskt och avståndet mellan två punkter A och B beräknas enligt följande:
d = √ [(xtill - xb)två + (Ytill - Yb)två + (ztill - zb)två]
Människor kan inte uppfatta mer än tre rumsliga (eller euklidiska) dimensioner.
Ur sträng matematisk synpunkt är det dock möjligt att definiera ett n-dimensionellt euklidiskt utrymme.
I detta utrymme har en punkt koordinater: (x1, x2, x3,…, xn) och avståndet mellan två punkter är:
d = √ [(x1: a - x1 B)två + (x2: a - x2b)två +... + (Xna - xnb)två].
Den fjärde dimensionen och tiden
I relativitetsteorin behandlas faktiskt tiden som en ytterligare dimension och en koordinat är associerad med den.
Men det måste klargöras att denna koordinat associerad med tiden är ett imaginärt tal. Därför är separationen av två punkter eller händelser i rymdtid inte euklidisk, utan följer snarare Lorentz-metriska.
En fyrdimensionell hyperkub (tesserakten) lever inte i rymdtid, den tillhör ett fyrdimensionellt euklidiskt hyperrum.

Koordinaterna för en hyperkub
Koordinaterna för hörnpunkterna för en n-kub centrerad vid ursprunget erhålls genom att göra alla möjliga permutationer av följande uttryck:
(a / 2) (± 1, ± 1, ± 1,…., ± 1)
Där a är längden på kanten.
-De volym av en n-kub av kant a är: (a / 2)n (tvån) = an.
-De längsta diagonalen är avståndet mellan motsatta hörnpunkter.
-Följande är motsatta hörn i en kvadrat: (-1, -1) och (+1, +1).
-Och i en Kub: (-1, -1, -1) och (+1, +1, +1).
-De längsta diagonalen av en n-kub mäter:
d = √ [1 - (- 1))två +… + (1 - (- 1))två] = √ [n 2två] = 2√n
I detta fall antogs sidan vara a = 2. För en n-kub på vilken sida som helst kommer följande att finnas kvar:
d = a√n.
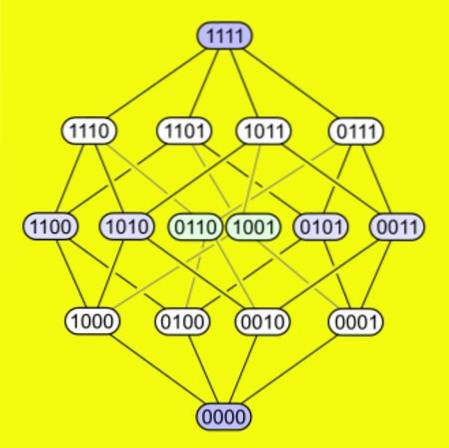
-En tesserakt har var och en av sina 16 hörn anslutna till fyra kanter. Följande bild visar hur hörn är kopplade i en tesserakt.
Vikning av en hyperkub
En vanlig geometrisk figur, till exempel en polyeder, kan vikas ut till flera figurer av mindre dimension.
När det gäller en 2-kub (en kvadrat) kan den vikas ut i fyra segment, det vill säga fyra 1-kub.
På samma sätt kan en 3-kub vikas ut i sex 2-kub.

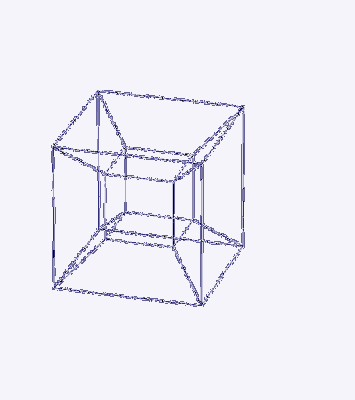
En 4-kub (tesseract) kan vikas ut till åtta 3-kub.
Följande animering visar hur en tesserakt utvecklas.

Referenser
- Vetenskaplig kultur. Hypercube, visualisering av den fjärde dimensionen. Återställd från: culturacientifica.com
- Epsilons. Fyrdimensionell hyperkub eller tesserakt. Återställd från: epsilones.com
- Perez R, Aguilera A. En metod för att få en tesserakt från utvecklingen av en hyperkub (4D). Återställd från: researchgate.net
- Wikibooks. Matematik, polyeder, hypercubes. Återställd från: es.wikibooks.org
- Wikipedia. Hypercube. Återställd från: en.wikipedia.com
- Wikipedia. Tesseract. Återställd från: en.wikipedia.com



Ingen har kommenterat den här artikeln än.