De homoscedasticitet i en prediktiv statistisk modell uppträder det om i alla datagrupperna för en eller flera observationer, variansen hos modellen med avseende på de förklarande (eller oberoende) variablerna förblir konstant.
En regressionsmodell kan vara homoscedastisk eller inte, i vilket fall vi talar om heteroscedasticitet.
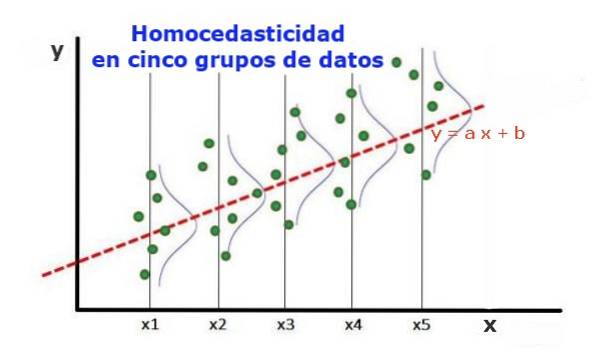
En statistisk regressionsmodell med flera oberoende variabler kallas homoscedastic, bara om variansen för felet hos den förutsagda variabeln (eller standardavvikelsen för den beroende variabeln) förblir enhetlig för olika gruppvärden för de förklarande eller oberoende variablerna.
I de fem datagrupperna i figur 1 har variansen i varje grupp beräknats med avseende på det värde som uppskattas av regressionen, vilket resulterar i att vara densamma i varje grupp. Det antas vidare att uppgifterna följer normalfördelningen.
På grafisk nivå betyder det att punkterna är lika utspridda eller utspridda runt det värde som förutses av regressionspassningen, och att regressionsmodellen har samma fel och giltighet för området för den förklarande variabeln..
Artikelindex
För att illustrera vikten av homoscedasticitet i prediktiv statistik är det nödvändigt att kontrastera med det motsatta fenomenet, heteroscedasticity.
I fallet med figur 1, där det finns homoscedasticitet, är det sant att:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈… Var ((y4-Y4); X4)
Där Var ((yi-Yi); Xi) representerar variansen representerar paret (xi, yi) data från grupp i, medan Yi är det värde som förutses av regressionen för medelvärdet Xi för gruppen. Variansen för n-data från grupp i beräknas enligt följande:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Tvärtom, när heteroscedasticitet inträffar kanske inte regressionsmodellen är giltig för hela regionen där den beräknades. Figur 2 visar ett exempel på denna situation.
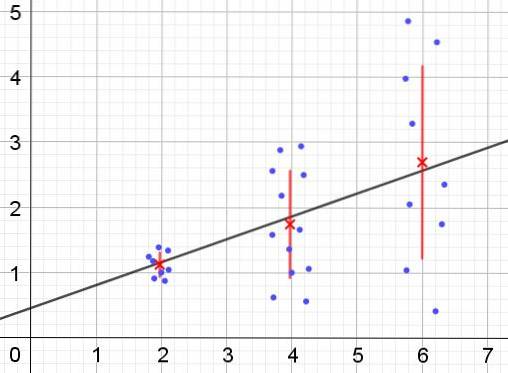
Figur 2 representerar tre datagrupper och uppsättningen av uppsättningen med hjälp av en linjär regression. Det bör noteras att data i den andra och tredje gruppen är mer spridda än i den första gruppen. Diagrammet i figur 2 visar också medelvärdet för varje grupp och dess felfält ± σ, med σ standardavvikelsen för varje datagrupp. Man bör komma ihåg att standardavvikelsen σ är variansroten.
Det är uppenbart att i fallet med heteroscedasticitet ändras regressionsuppskattningsfelet i värden för den förklarande eller oberoende variabeln, och i intervallen där detta fel är mycket stort är regressionsförutsägelsen opålitlig eller inte tillämplig.
I en regressionsmodell måste felen eller resterna (och -Y) fördelas med samma varians (σ ^ 2) genom hela intervallet för värden för den oberoende variabeln. Det är av denna anledning som en bra regressionsmodell (linjär eller icke-linjär) måste klara homoscedasticitetstestet..
Poängen som visas i figur 3 motsvarar data från en studie som letar efter en relation mellan huspriserna (i dollar) som en funktion av storleken eller arean i kvadratmeter.
Den första modellen som testas är en linjär regression. För det första noteras det att bestämningskoefficienten R ^ 2 för passningen är ganska hög (91%), så man kan tro att passningen är tillfredsställande..
Två regioner kan emellertid tydligt skiljas från justeringsdiagrammet. En av dem, den till höger innesluten i en oval, uppfyller homoscedasticitet, medan regionen till vänster inte har homoscedasticity.
Detta innebär att förutsägelsen för regressionsmodellen är adekvat och tillförlitlig i intervallet 1800 m ^ 2 till 4800 m ^ 2 men mycket otillräcklig utanför denna region. I den heteroscedastiska zonen är inte bara felet mycket stort, utan också uppgifterna verkar följa en annan trend än den som föreslås av den linjära regressionsmodellen..
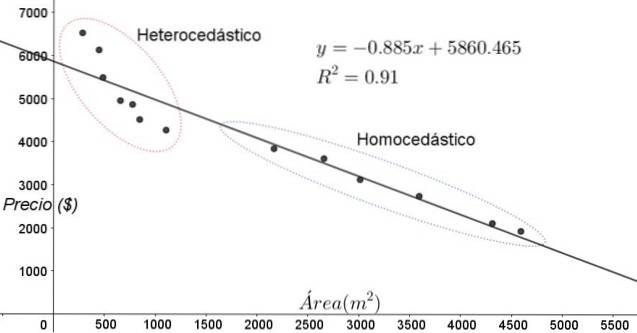
Spridningsdiagrammet för data är det enklaste och mest visuella testet av deras homoscedasticitet, men vid tillfällen där det inte är så uppenbart som i exemplet som visas i figur 3 är det nödvändigt att tillgripa diagram med hjälpvariabler..
För att separera områdena där homoscedasticitet uppfylls och där den inte är, introduceras de standardiserade variablerna ZRes och ZPred:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Det bör noteras att dessa variabler beror på den tillämpade regressionsmodellen, eftersom Y är värdet på regressionsprognosen. Nedan är spridningsdiagrammet ZRes vs ZPred för samma exempel:
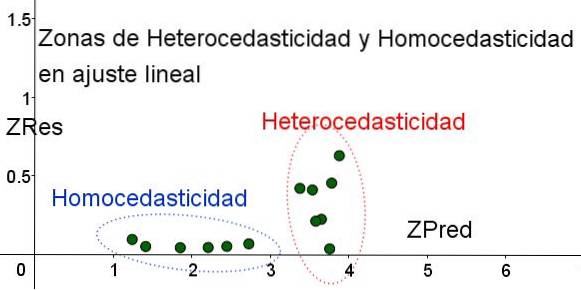
I diagrammet i figur 4 med standardiserade variabler är området där restfelet är litet och enhetligt klart åtskilt från området där det inte är. I den första zonen uppfylls homoscedasticitet medan i det område där restfelet är mycket varierande och stort uppfylls heteroscedasticity..
Regressionsjustering tillämpas på samma datagrupp i figur 3, i detta fall är justeringen icke-linjär, eftersom den använda modellen innefattar en potentiell funktion. Resultatet visas i följande bild:
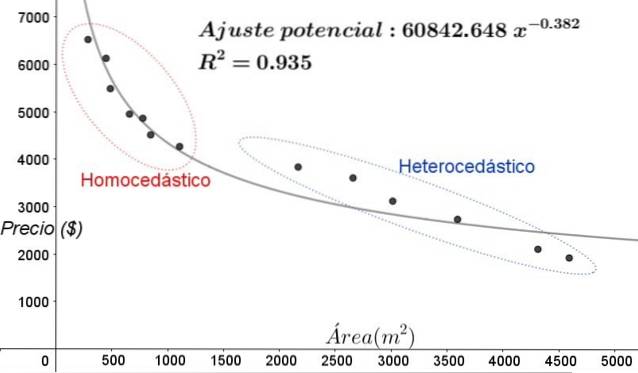
I diagrammet i figur 5 bör homoscedastiska och heteroscedastiska zoner noteras tydligt. Det bör också noteras att dessa zoner utbyttes i förhållande till de som bildades i linjär passformmodell.
I diagrammet i figur 5 är det uppenbart att även om det finns en ganska hög bestämningskoefficient för passformen (93,5%) är modellen inte tillräcklig för hela intervallet för den förklarande variabeln, eftersom data för värden större än 2000 m ^ 2 nuvarande heteroscedasticitet.
En av de icke-grafiska tester som mest används för att verifiera om homoscedasticitet är uppfyllt eller inte är Breusch-Pagan test.
Inte alla detaljer i detta test kommer att ges i den här artikeln, men dess grundläggande egenskaper och stegen i samma beskrivs i stora drag:
De flesta av de statistiska mjukvarupaket som: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic och flera andra innehåller homoscedasticitetstest av Breusch-Pagan. Ett annat test för att verifiera enhetlighet i varians Levene-test.
Ingen har kommenterat den här artikeln än.