Mått på central tendens för grupperade dataformler, övningar

De trendmått central de anger värdet kring vilket data för en distribution är. Det mest kända är det genomsnittliga eller aritmetiska medelvärdet, som består av att lägga till alla värden och dela resultatet med det totala antalet data.

Men om distributionen består av ett stort antal värden och de inte presenteras på ett ordnat sätt är det inte lätt att utföra de nödvändiga beräkningarna för att extrahera den värdefulla informationen de innehåller..

Det är därför de är grupperade i klasser eller kategorier för att utveckla en distribution av frekvenser. Genom att utföra denna tidigare beställning av data är det lättare att beräkna måtten på den centrala tendensen, bland annat:

-Halv

-Median

-mode

-Geometriskt medelvärde

-Harmoniskt medelvärde

Formler

Här är formlerna för måtten på den centrala tendensen för de grupperade data:

Aritmetiskt medelvärde

Medlet är det mest använda för att karakterisera kvantitativa data (numeriska värden), även om det är ganska känsligt för distributionens extrema värden. Det beräknas av:

Med:

-X: medelvärde eller aritmetiskt medelvärde

-F_i: klassfrekvens

-m_i: klassmärket

-g: antal klasser

-n: totala data

Median

För att beräkna det är det nödvändigt att hitta intervallet som innehåller observationen n / 2 och interpolera för att bestämma det numeriska värdet för nämnda observation med hjälp av följande formel:

Var:

-c: bredden på det intervall som medianen tillhör

-B_M: nedre gräns för nämnda intervall

-F_m: antal observationer som ingår i intervallet

-n / 2: totala data dividerat med 2.

-F_BM: antal observationer innan av intervallet som innehåller medianen.

Därför är medianen ett mått på position, det vill säga det delar upp datamängden i två delar. De kan också definieras kvartiler, deciler Y percentiler, som delar fördelningen i fyra, tio respektive hundra delar.

mode

I de samlade uppgifterna söks den klass eller kategori som innehåller flest observationer. Det här är modal klass. En distribution kan ha två eller flera lägen, i vilket fall den kallas bimodal Y multimodal, respektive.

Du kan också beräkna läget i grupperade data enligt ekvationen:

Med:

-L₁: nedre gräns för klassen där läget finns

-Δ₁: subtrahera mellan modalklassens frekvens och frekvensen för den klass som föregår den.

-Δ_två: subtrahera mellan modalklassens frekvens och frekvensen för nästa klass.

-c: bredden på intervallet som innehåller läget

Harmoniskt medelvärde

Det harmoniska medelvärdet betecknas med H. När du har en uppsättning n x-värden₁, x_två, x₃..., Det harmoniska medelvärdet är det omvända eller ömsesidiga av det aritmetiska medelvärdet av de inversa värdena.

Det är lättare att se det genom formeln:

Och med den grupperade informationen tillgänglig blir uttrycket:

Var:

-H: harmoniskt medelvärde

-F_i: klassfrekvens

-m_i: klassmärke

-g: antal klasser

-N = f₁ + F_två + F₃ +...

Geometriskt medelvärde

Om de har n positiva tal x₁, x_två, x₃…, Dess geometriska medelvärde G beräknas av produktens n: te rot av alla siffror:

När det gäller grupperade data kan det visas att decimallogaritmen för den geometriska medelloggen G ges av:

Var:

-G: geometriskt medelvärde

-F_i: klassfrekvens

-m_i: klassmärket

-g: antal klasser

-N = f₁ + F_två + F₃ +...

Förhållandet mellan H, G och X

Det är alltid sant att:

H ≤ G ≤ X

Mest använda definitioner

Följande definitioner krävs för att hitta värdena som beskrivs i formlerna ovan:

Frekvens

Frekvens definieras som antalet gånger en bit data upprepas.

Rang

Det är skillnaden mellan de högsta och lägsta värdena som finns i fördelningen.

Antal klasser

För att veta i hur många klasser vi grupperar data använder vi några kriterier, till exempel följande:

Gränser

De extrema värdena för varje klass eller intervall kallas gränser och varje klass kan ha båda väldefinierade gränser, i vilket fall den har en lägre och en högre gräns. Eller så kan det ha öppna gränser när ett intervall anges, till exempel värden som är större eller mindre än ett visst antal.

Klassmärke

Den består helt enkelt av mittpunkten för intervallet och beräknas genom medelvärdet av den övre och undre gränsen.

Gapbredd

Data kan grupperas i klasser av lika eller olika storlek, detta är bredden eller bredden. Det första alternativet är det mest använda, eftersom det gör beräkningar mycket enklare, även om det i vissa fall är absolut nödvändigt att klasserna har olika bredd.

Bredden c Intervallet kan bestämmas med följande formel:

c = Räckvidd / N_c

Var_c är antalet klasser.

Övningen löst

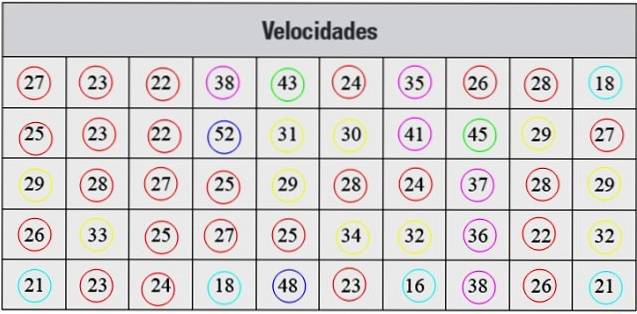
Nedan har vi en serie hastighetsmätningar i km / h, tagna med radar, som motsvarar 50 bilar som passerade genom en gata i en viss stad:

Lösning

De data som presenteras på detta sätt är inte organiserade, så det första steget är att gruppera dem i klasser.

Steg för att gruppera data och skapa tabellen

Steg 1

Hitta intervallet R:

R = (52 - 16) km / h = 36 km / h

Steg 2

Välj antal klasser N_c, enligt givna kriterier. Eftersom det finns 50 data kan vi välja N_c = 6.

Steg 3

Beräkna bredd c av intervallet:

c = Område / N._c = 36/6 = 6

Steg 4

Formklasser och gruppdata enligt följande: för den första klassen väljs ett värde som är något mindre än det lägsta värdet i tabellen som den undre gränsen, sedan läggs värdet på c = 6, tidigare beräknat, till detta värde, alltså uppnår den första klassens övre gräns.

Vi fortsätter på samma sätt för att bygga resten av klasserna, som visas i följande tabell:

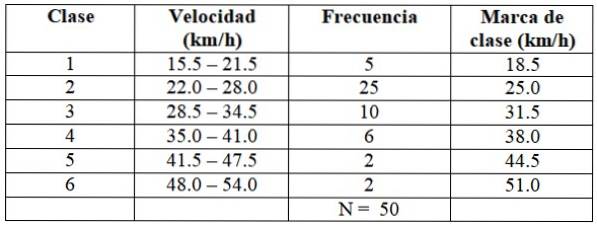
Varje frekvens motsvarar en färg i figur 2, på detta sätt säkerställs att inget värde slipper räknas..

Beräkning av medelvärdet

X = (5 x 18,5 +25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / h

Beräkning av medianen

Medianen är i klass 2 i tabellen, eftersom det finns de första 30 data för distributionen.

-Bredden på det intervall som medianen tillhör: c = 6

-Nedre gräns för intervallet där medianen är: B_M = 22,0 km / h

-Antal observationer som intervallet f innehåller_m = 25

-Totala data dividerat med 2: 50/2 = 25

-Antal observationer som finns innan av intervallet som innehåller medianen: f_BM = 5

Och operationen är:

Median = 22,0 + [(25-5) ÷ 25] × 6 = 26,80 km / h

Mode beräkning

Mode är också i klass 2:

-Intervallbredd: c = 6

-Nedre gräns för klassen där läget finns: L₁ = 22,0

-Subtrahera mellan modalklassens frekvens och frekvensen för den klass som föregår den: Δ₁ = 25-5 = 20

-Subtrahera mellan modalklassens frekvens och frekvensen för klassen som följer: Δ_två = 25 - 10 = 15

Med dessa data är operationen:

Läge = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / h

Beräkning av det geometriska medelvärdet

N = f₁ + F_två + F₃ +... = 50

logg = (5 x log 18,5 + 25 x log 25 + 10 x log 31,5 + 6 x log 38 + 2 × log 44,5 + 2 x log 51) / 50 =

logg G = 1,44916053

G = 28,13 km / h

Harmonisk medelberäkning

1 / H = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366

H = 27,32 km / h

Sammanfattning av mått på central tendens

Enheterna för variablerna är km / h:

-Genomsnitt: 29.03

-Median: 26.80

-Mode: 25.40

-Geometriskt medelvärde: 28,13

-Harmoniskt medelvärde: 27,32

Referenser

1. Berenson, M. 1985. Statistik för management och ekonomi. Interamericana S.A.
2. Canavos, G. 1988. Sannolikhet och statistik: Tillämpningar och metoder. Mcgraw hill.
3. Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
4. Levin, R. 1988. Statistik för administratörer. 2: a. Utgåva. Prentice hall.
5. Spiegel, M. 2009. Statistik. Schaum-serien. 4: e Utgåva. Mcgraw hill.
6. Behandling av grupperade data. Återställd från: itchihuahua.edu.mx.
7. Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.