Tröghetsmomentformler, ekvationer och beräkningsexempel

De tröghetsmoment av en stel kropp i förhållande till en viss rotationsaxel, representerar dess motstånd mot att ändra dess vinkelhastighet runt nämnda axel. Det är proportionellt mot massan och också till platsen för rotationsaxeln, eftersom kroppen enligt sin geometri kan rotera lättare runt vissa axlar än i andra.

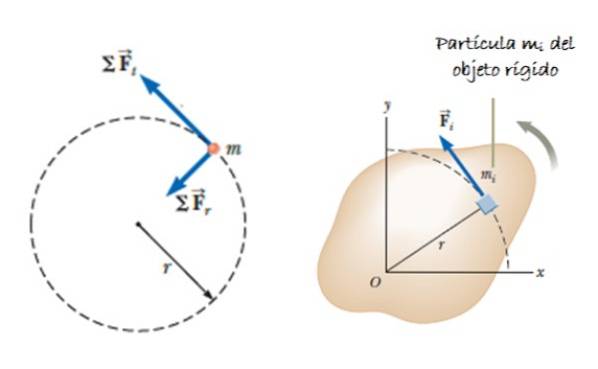
Anta ett stort föremål (bestående av många partiklar) som kan rotera runt en axel. Antag att en kraft verkar F, appliceras tangentiellt på masselementet Am_i, som producerar ett vridmoment eller moment, givet av τ_netto = ∑r_i x F_i. Vektoren r_i är positionen för Am_i (se figur 2).

Detta ögonblick är vinkelrätt mot rotationsplanet (riktning +k = kommer ut ur tidningen). Eftersom kraften och den radiella lägesvektorn alltid är vinkelräta förblir korsprodukten:

τ_netto = ∑ F_i r_i k = ∑ (Δm_i till_i) r_i  k = ∑ Δm_i (till_i r_i ) k

Acceleration till_i representerar den tangentiella komponenten av acceleration, eftersom radiell acceleration inte bidrar till vridmoment. Som en funktion av vinkelacceleration α kan vi indikera att:

till_i = a r_i

Därför ser nettomomentet ut så här:

τ_netto = ∑ Δm_i (a r_i^två) k = (∑ r_i^två Am_i) a k

Vinkelacceleration α är densamma för hela objektet, därför påverkas det inte av abonnemanget "i" och kan lämna summeringen, vilket är exakt tröghetsmomentet för objektet som symboliseras av bokstaven I:

I = ∑ r_i^två Am_i

Detta är tröghetsmomentet för en diskret massfördelning. När distributionen är kontinuerlig ersätts summeringen med en integral och Am blir en massdifferential dm. Integralen utförs över hela objektet:

Jag = ∫_M(r^två) dm

Enheterna för tröghetsmomentet i SI International System är kg x m^två. Det är en skalär och positiv kvantitet, eftersom den är produkten av en massa och ett kvadrat av ett avstånd.

Artikelindex

• 1 Beräkningsexempel
  • 1.1 Tröghetsmoment för en tunn stång med avseende på en axel som passerar genom dess centrum
  • 1.2 Tröghetsmoment för en skiva med avseende på en axel som passerar genom dess centrum
  • 1.3 Tröghetsmoment för en fast sfär med avseende på en diameter
  • 1.4 Tröghetsmoment för en solid cylinder i förhållande till den axiella axeln
  • 1.5 Tröghetsmoment för ett rektangulärt ark med avseende på en axel som passerar genom dess centrum
  • 1.6 Tröghetsmoment för ett fyrkantigt ark i förhållande till en axel som passerar genom dess centrum
• 2 Tröghetssatser
  • 2.1 Steiners teorem
  • 2.2 Vinkelräta axlar
• 3 Övningen löst
• 4 Referenser

Beräkningsexempel

Ett utökat objekt, såsom en stapel, skiva, sfär eller annat vars densitet ρ är konstant och att veta att densiteten är mass-volym-förhållandet, massdifferensen dm skrivs som:

ρ = dm / dV → dm = ρdV

Att ersätta integralen för tröghetsmomentet har vi:

I = ∫r^två ρdV = ρ ∫r^tvådV

Detta är ett allmänt uttryck, giltigt för ett tredimensionellt objekt vars volym V och position r är funktioner för de geografiska koordinaterna x, Y Y z. Observera att eftersom densiteten är konstant, ligger densiteten utanför integralen.

Densiteten ρ Det är också känt som volumetrisk densitet, men om objektet är väldigt platt, som ett ark eller väldigt tunt och smalt som en stav, kan andra former av densitet användas, låt oss se:

- För ett mycket tunt ark är densiteten att använda σ, ytdensiteten (massa per ytenhet) och ger är areaskillnaden.

- Och om det är en tunn stapel, där endast längden är relevant, används den linjära massdensiteten λ och en längdskillnad enligt den axel som används som referens.

I följande exempel anses alla föremål vara styva (inte deformerbara) och ha enhetlig densitet.

Tröghetsmoment för en tunn stång med avseende på en axel som passerar genom dess centrum

Här ska vi beräkna tröghetsmomentet för en tunn, stel, homogen stapel med längd L och massa M, med avseende på en axel som passerar genom mitten.

Först är det nödvändigt att etablera ett koordinatsystem och bygga en figur med lämplig geometri, så här:

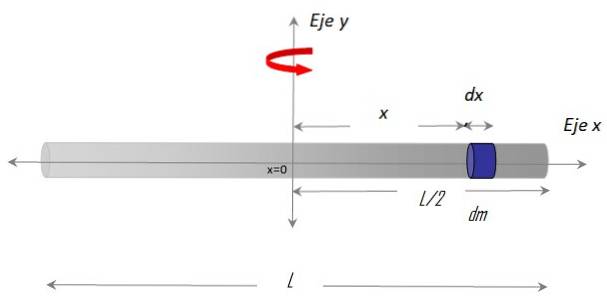
De X-axeln längs baren och Axel y som rotationsaxeln. Proceduren för att fastställa integralen kräver också att man väljer en massdifferens över stapeln dm, som har en differentiell längd dx och ligger på positionen x godtyckligt i förhållande till centrum x = 0.

Enligt definitionen av linjär massdensitet λ:

λ = M / L

Eftersom densiteten är enhetlig, vilket gäller för M och L, gäller den också för dm och dx:

λ = dm / dx → dm = λdx.

Å andra sidan är masselementet i position x, sedan genom att ersätta denna geometri i definitionen har vi en bestämd integral, vars gränser är ändarna på stapeln enligt koordinatsystemet:

Ersätter den linjära densiteten λ = M / L:

För att hitta stångens tröghetsmoment i förhållande till en annan rotationsaxel, till exempel en som passerar genom en av dess ytterligheter, kan du använda Steiners sats (se övning löst i slutet) eller utföra en direkt beräkning som liknar den visas här, men ändrar geometrin på lämpligt sätt.

Tröghetsmoment för en skiva med avseende på en axel som passerar genom dess centrum

En mycket tunn skiva med försumbar tjocklek är en platt figur. Om massan fördelas jämnt över hela ytan av område A är massdensiteten σ:

σ = M / Y

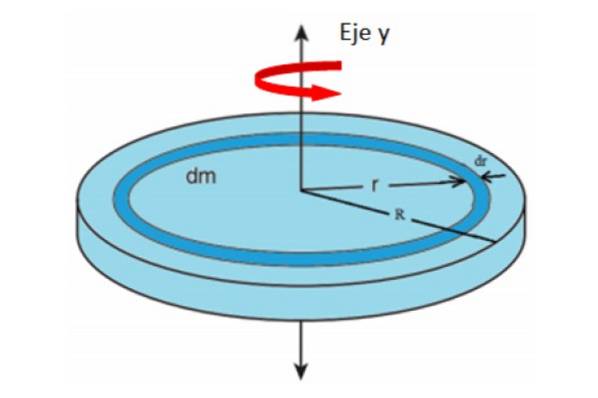
Så mycket dm Vad ger motsvarar massan och arean av differentialringen som visas i figuren. Vi antar att hela enheten roterar runt y-axeln.

Du kan föreställa dig att skivan består av många koncentriska ringar med radie r, var och en med sitt respektive tröghetsmoment. Lägg till bidrag från alla ringar tills radien når R, det totala tröghetsmomentet för skivan kommer att vara.

σ = dm / dA → dm = σger

Där M representerar hela skivans massa. Skivans område beror på dess radie r som:

A = π.r^två

Härleda med avseende på r:

dA / dr = 2 = 2π.r → dA = 2π.rdr

Ersätter ovan i definitionen av I:

Ersätter σ = M / (π.R^två ) resterna:

Tröghetsmoment för en fast sfär med avseende på en diameter

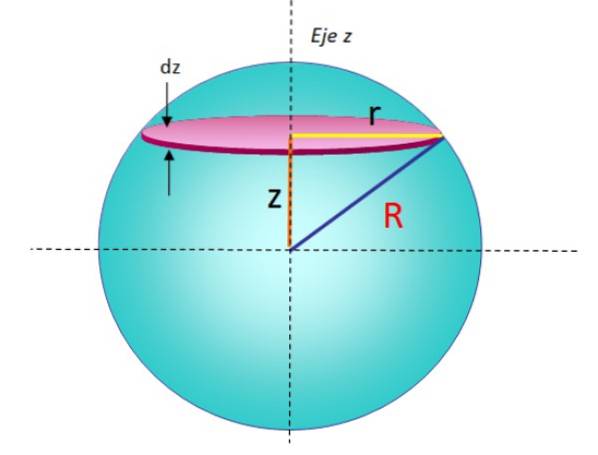
En sfär med radie R kan ses som en serie skivor staplade ovanpå varandra, där varje skiva med oändlig massa dm, radio r och tjocklek dz, har ett tröghetsmoment som ges av:

gav_disk = (½) r^tvådm

För att hitta denna skillnad tog vi helt enkelt formeln från föregående avsnitt och ersatte M Y R för dm Y r, respektive. En sådan skiva kan ses i geometrin i figur 5.

Genom att lägga till alla oändliga tröghetsmoment för staplade skivor erhålls sfärens totala tröghetsmoment:

Jag_sfär = ∫dI_disk

Vilket motsvarar:

Jag = ∫_sfär (½) r^tvådm

För att lösa integralen måste du uttrycka dm ordentligt. Som alltid uppnås det från densiteten:

ρ = M / V = ​​dm / dV → dm = ρ.dV

Volymen på en differentiell skiva är:

dV = Basarea x höjd

Skivans höjd är tjockleken dz, medan basområdet är πr^två, Således:

dV = πr^tvådz

Och att ersätta den föreslagna integralen skulle det se ut så här:

Jag = ∫_sfär(½) r^tvådm = ∫ (½) r^två(ρπr^tvådz)

Men innan vi integrerar måste det observeras att r-skivans radie beror på z och R-sfärens radie, vilket framgår av figur 5. Använda Pythagoras sats:

R^två = r^två + z^två → r^två = R^två - z^två

 Vilket leder oss till:

Jag = ∫_sfär(½) ρ r^två(πr^tvådz) = ∫_sfär(½) ρ π r⁴dz= ∫_sfär(½) ρ π (R^två - z^två)^två dz

För att integrera över hela sfären noterar vi att z varierar mellan -R och R, därför:

Veta att ρ = M / V = ​​M / [(4/3) πR³] äntligen erhålls det, efter att ha förenklat:

Tröghetsmoment för en solid cylinder i förhållande till den axiella axeln

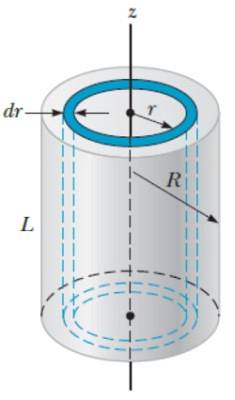
För detta objekt används en metod som liknar den som används för sfären, bara den här gången är det lättare om cylindern föreställs bildas av cylindriska skal med radie r, tjocklek dr och höjd H, som om de vore lager av en lök.

Volymen dV av ett cylindriskt skikt är:

dV = 2π.rL.dr

Därför är skalmassan:

dm = ρ.dV = ρ. 2π.r.L.dr

Detta uttryck ersätts i definitionen av tröghetsmoment:

Ovanstående ekvation indikerar att cylinderns tröghetsmoment inte beror på dess längd utan bara på dess massa och radie. Ja L ändras, skulle tröghetsmomentet om den axiella axeln förbli densamma. Av denna anledning, Jag av cylindern sammanfaller med den för den tidigare beräknade tunna skivan.

Tröghetsmoment för ett rektangulärt ark med avseende på en axel som passerar genom dess centrum

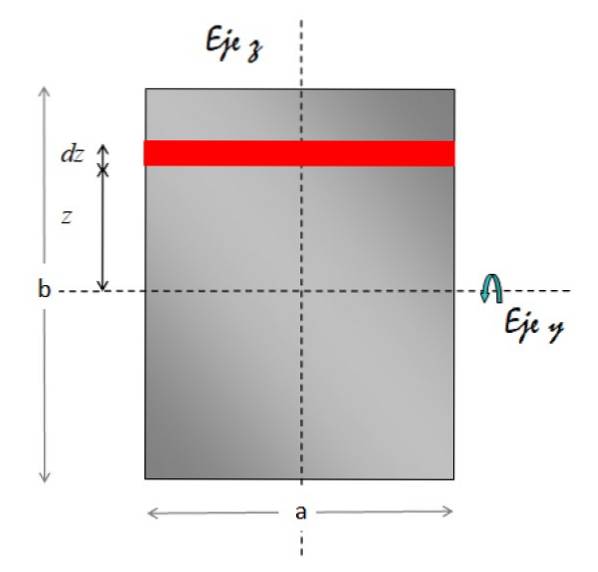
De Axel y horisontell rotationsaxel. Figuren nedan visar geometrin som krävs för att genomföra integrationen:

Områdeselementet markerat med rött är rektangulärt. Dess yta är bas x höjd, därför:

dA = a.dz

Därför är massdifferensen:

dm = σ.dA = σ. (a.dz)

När det gäller avståndet från areaelementet till rotationsaxeln är det alltid z. Vi ersätter allt detta med integriteten av tröghetsmomentet:

Nu ersätts ytmassans densitet σ med:

σ = M / ab

Och det ser definitivt ut så här:

Observera att den är som den med den tunna stången.

Tröghetsmoment för ett fyrkantigt ark med avseende på en axel som passerar genom dess centrum

För en sidoruta L, i det föregående uttrycket giltigt för en rektangel, ersätt helt enkelt värdet på b för den av L:

Moment av tröghetssatser

Det finns två satser som är särskilt användbara för att förenkla beräkningen av tröghetsmoment om andra axlar, som annars kan vara svåra att hitta på grund av brist på symmetri. Dessa satser är:

Steiners sats

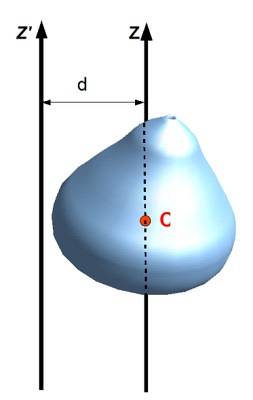
Även kallad sats för parallella axlar, relaterar tröghetsmomentet med avseende på en axel med en annan som passerar genom objektets masscentrum så länge axlarna är parallella. För att tillämpa det är det nödvändigt att känna avståndet D mellan båda axlarna och naturligtvis objektets massa M.

Vara Jag_z tröghetsmomentet för ett utökat objekt med avseende på z-axeln, jag_CENTIMETER tröghetsmomentet med avseende på en axel som passerar genom masscentrum (CM) för nämnda objekt, så är det sant att:

Jag_z = Jag_CENTIMETER + MD^två

Eller i noteringen av följande bild: Jag_{z '} = Jag_z + Md^två

Vinkelräta axlar sats

Denna sats tillämpas på plana ytor och går så här: ett planobjektets tröghetsmoment runt en axel vinkelrät mot det är summan av tröghetsmomenten runt två axlar vinkelrätt mot den första axeln:

Jag_z = Jag_x + Jag_Y

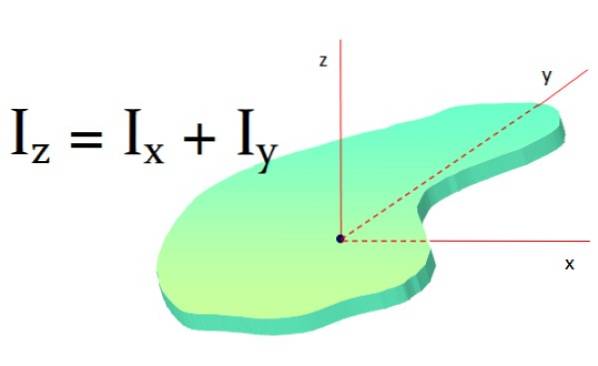
Om objektet har symmetri så att Jag_x och Jag_Y är lika, då är det sant att:

Jag_z = 2I_x

Övningen löst

Hitta tröghetsmomentet för stången med avseende på en axel som passerar genom en av dess ändar, som visas i figur 1 (nedan och till höger) och figur 10.

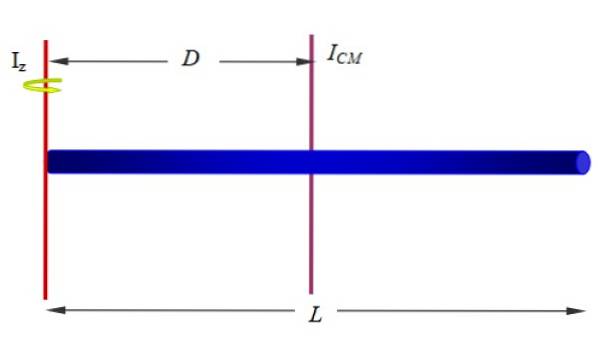
Lösning:

Vi har redan tröghetsmomentet för stapeln runt en axel som passerar genom dess geometriska centrum. Eftersom stapeln är homogen är dess masscentrum vid den punkten, så detta kommer att bli vårt Jag_CENTIMETER att tillämpa Steiners sats.

Om längden på stången är L, z-axeln är på ett avstånd D = L / 2, därför:

Jag_z = Jag_CENTIMETER + MD^två= (1/12) ML^två+M (L / 2)^två= (1/3) ML^två

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 313-340
2. Rex, A. 2011. Grundläggande fysik. Pearson. 190-200.
3. Parallell axelteorem. Återställd från: hyperphysics.phy-astr.gsu.edu.
4. Serway, R. 2018. Fysik för vetenskap och teknik. Volym 1. Cengage.
5. Sevilla universitet. Tröghetsmoment för sfäriska fasta ämnen. Återställd från: laplace.us.es.
6. Sevilla universitet. Tröghetsmoment för ett partikelsystem. Återställd från: laplace.us.es.
7. Wikipedia. Sats för parallellaxel. Återställd från: en.wikipedia.org