
Nullvinkeldefinition och egenskaper, exempel, övningar
De null vinkel Det är ett vars mått är 0, både i grader och i radianer eller ett annat system för vinkelmätning. Därför saknar den bredd eller öppning, såsom den som bildas mellan två parallella linjer..
Även om dess definition låter tillräckligt enkel, är nollvinkeln mycket användbar i många fysik- och teknikapplikationer, såväl som inom navigering och design..
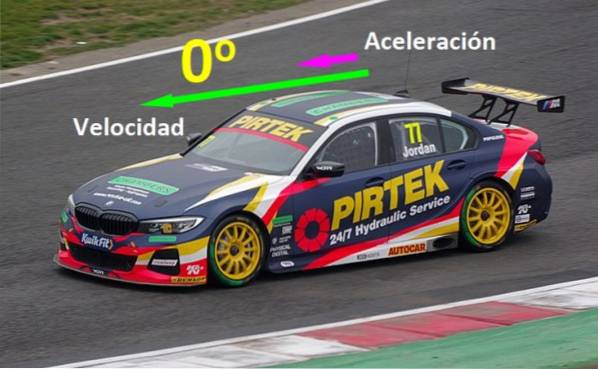
Det finns fysiska mängder som måste justeras parallellt för att uppnå vissa effekter: om en bil rör sig i en rak linje på en motorväg och matar in dess hastighetsvektor v och dess accelerationsvektor till det är 0º, bilen rör sig snabbare och snabbare, men om bilen bromsar är dess acceleration motsatt dess hastighet (se figur 1).
Följande bild visar olika typer av vinkel inklusive nollvinkeln till höger. Som framgår saknar 0º-vinkeln bredd eller öppning..

Artikelindex
- 1 Exempel på nollvinklar
- 1.1 - Nollvinkelns effekter på fysiska storheter
- 2 övningar
- 2.1 - Övning 1
- 2.2 - Övning 2
- 3 Referenser
Exempel på nollvinklar
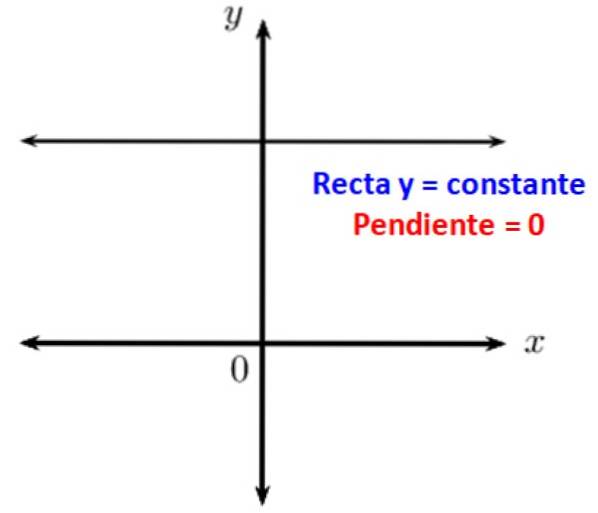
Parallella linjer är kända för att bilda en nollvinkel med varandra. När du har en horisontell linje är den parallell med x-axeln för det kartesiska koordinatsystemet, därför är dess lutning i förhållande till den 0. Med andra ord har horisontella linjer nolllutning.
Även de trigonometriska förhållandena för nollvinkeln är 0, 1 eller oändlighet. Därför är nollvinkeln närvarande i många fysiska situationer som involverar operationer med vektorer. Dessa skäl är:
-sin 0º = 0
-cos 0º = 1
-tg 0º = 0
-sek 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
Och de kommer att vara användbara för att analysera några exempel på situationer där närvaron av nollvinkeln spelar en grundläggande roll:
- Nollvinkelns effekter på fysiska mängder
Vector tillägg
När två vektorer är parallella är vinkeln mellan dem noll, vilket framgår av figur 4a ovan. I detta fall utförs summan av båda genom att placera varandra efter varandra och storleken på summeringsvektorn är summan av storleken på tillsatserna (figur 4b).

När två vektorer är parallella är vinkeln mellan dem noll, vilket framgår av figur 4a ovan. I detta fall utförs summan av båda genom att placera varandra efter varandra och storleken på summeringsvektorn är summan av storleken på tillsatserna (figur 4b)
Momentet eller vridmomentet
Momentet eller vridmomentet orsakar en kropps rotation. Det beror på storleken på den applicerade kraften och hur den appliceras. Ett mycket representativt exempel är skiftnyckeln i figuren.
För att uppnå bästa vridningseffekt appliceras kraften vinkelrätt mot nyckelhandtaget, antingen uppåt eller nedåt, men ingen rotation förväntas om kraften är parallell med handtaget..
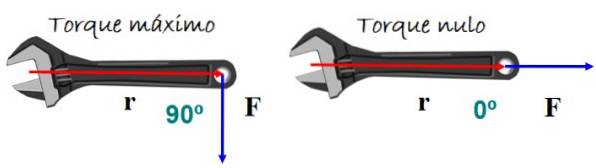
Matematiskt vridmoment τ definieras som tvärprodukt eller tvärprodukt mellan vektorer r (positionsvektor) och F (kraftvektor) från figur 5:
τ = r x F
Vridmomentets storlek är:
τ = r F sin θ
Där θ är vinkeln mellan r Y F. När sin θ = 0 är vridmomentet noll, i detta fall θ = 0º (eller även 180 °).
Elektriskt fältflöde
Det elektriska fältflödet är en skalär storlek som beror på det elektriska fältets intensitet och orienteringen på ytan genom vilken den passerar..
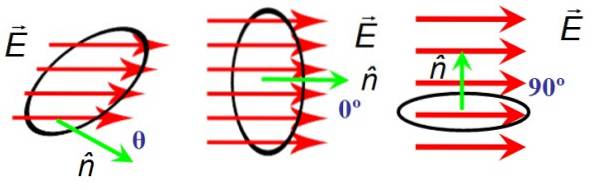
I figur 6 finns en cirkulär yta av område A genom vilken de elektriska fältlinjerna passerar OCH. Ytans orientering ges av den normala vektorn n. Till vänster bildar fältet och den normala vektorn en godtycklig spetsig vinkel θ, i mitten bildar de en nollvinkel med varandra och till höger är de vinkelräta.
När OCH Y n är vinkelräta passerar fältlinjerna inte ytan och därför är flödet noll, medan när vinkeln mellan OCH Y n är noll, linjerna passerar helt ytan.
Att beteckna det elektriska fältflödet med den grekiska bokstaven Φ (läs "fi"), dess definition för ett enhetligt fält som i figuren, ser ut så här:
Φ = OCH•nTILL
Punktet i mitten av båda vektorerna betecknar punktprodukten eller punktprodukten, som alternativt definieras enligt följande:
Φ = OCH•nA = EAcosθ
Fet och pilarna ovanför bokstaven är resurser för att skilja mellan en vektor och dess storlek, vilket betecknas med normala bokstäver. Eftersom cos 0 = 1 är flödet maximalt när OCH Y n de är parallella.
Träning
- Övning 1
Två krafter P Y F agera samtidigt på ett punktobjekt X, båda krafterna bildar initialt en vinkel θ mellan dem. Vad händer med den resulterande kraftens storlek när θ minskar till noll?
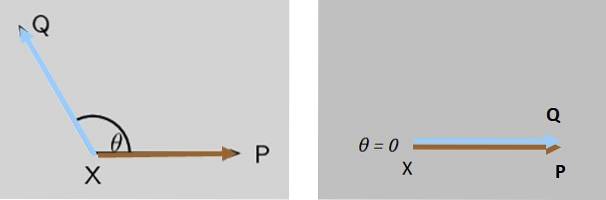
Lösning
Storleken på den resulterande kraften F + P gradvis ökar tills det är maximalt när F Y P är helt parallella (figur 7 till höger).
- Övning 2
Ange om nollvinkeln är en lösning av följande trigonometriska ekvation:
cos 2x = 1 + 4 sin x
Lösning
En trigonometrisk ekvation är en där det okända är en del av argumentet för ett trigonometriskt förhållande. För att lösa den föreslagna ekvationen är det bekvämt att använda formeln för cosinus med dubbel vinkel:
cos 2x = costvå x - syndtvå x
För på detta sätt blir argumentet på vänster sida x istället för 2x. Sedan:
costvå x - syndtvå x = 1 + 4sin x
Å andra sidan costvå x + syndtvå x = 1, så:
costvå x - syndtvå x = costvå x + syndtvå x + 4sen x
Termen costvå x avbryts och förblir:
- sentvå x = syndtvå x + 4sen x → - 2sentvå x - 4senx = 0 → 2sentvå x + 4senx = 0
Nu görs följande variabeländring: sinx = u och ekvationen blir:
2utvå + 4u = 0
2u (u + 4) = 0
Vilka lösningar är: u = 0 och u = -4. Om vi returnerar ändringen skulle vi ha två möjligheter: sin x = 0 och sinx = -4. Den sista lösningen är inte livskraftig, eftersom sinus i vilken vinkel som helst är mellan -1 och 1, så vi har kvar det första alternativet:
sin x = 0
Därför är x = 0º en lösning, men alla vinklar vars sinus är 0 fungerar också, vilket också kan vara 180 ° (π radianer), 360 ° (2 π radianer) och respektive negativ också.
Den mest allmänna lösningen av den trigonometriska ekvationen är: x = kπ där k = 0, ± 1, ± 2, ± 3,…. k ett heltal.
Referenser
- Baldor, A. 2004. Plan- och rymdgeometri med trigonometri. Publicaciones Cultural S.A. de C.V. Mexiko.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 3. Partikelsystem. Redigerad av Douglas Figueroa (USB).
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 5. Elektrisk interaktion. Redigerad av Douglas Figueroa (USB).
- OnlineMathLearning. Typer av vinklar. Återställd från: onlinemathlearning.com.
- Zill, D. 2012. Algebra, trigonometri och analytisk geometri. McGraw Hill Interamericana.

Ingen har kommenterat den här artikeln än.