
Sammansatta talegenskaper, exempel, övningar
De sammansatta nummer är de heltal som har mer än två delare. Om vi tittar noga är alla nummer åtminstone delbara exakt för sig själva och med 1. De som bara har dessa två delare kallas primtal, och de som har mer är föreningar..
Låt oss titta på siffran 2, som bara kan delas mellan 1 och 2. Siffran 3 har också två delare: 1 och 3. Därför är de båda primära. Låt oss nu titta på siffran 12, som vi kan dela exakt med 2, 3, 4, 6 och 12. Genom att ha 5 delare är 12 ett sammansatt tal.
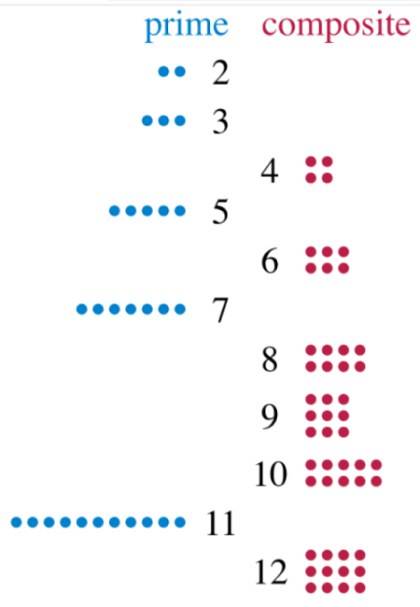
Och vad händer med siffran 1, den som delar upp alla andra? Tja, det är inte prime, eftersom det inte har två delare, och det är inte sammansatt, därför faller 1 inte in i någon av dessa två kategorier. Men det finns många, många fler siffror som gör det..
Sammansatta tal kan uttryckas som produkten av primtal, och denna produkt, förutom faktorernas ordning, är unik för varje nummer. Detta säkerställs av den grundläggande satsen för aritmetik som bevisats av den grekiska matematikern Euklid (325-365 f.Kr.).
Låt oss gå tillbaka till nummer 12, som vi kan uttrycka på olika sätt. Låt oss prova några:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2två x 3 = 3 x 2två = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Formerna som är markerade med fetstil är produkter med primtal och det enda som ändras är faktornas ordning, som vi vet inte förändrar produkten. De andra formerna, även om de är giltiga för att uttrycka 12, består inte enbart av primtal.
Exempel på sammansatta tal
Om vi vill sönderdela ett sammansatt tal i dess primfaktorer, måste vi dela det mellan primtal på ett sådant sätt att uppdelningen är exakt, det vill säga att resten är 0.
Denna procedur kallas primtalsfaktorisering eller kanonisk nedbrytning. Primära faktorer kan höjas till positiva exponenter.
Vi kommer att sönderdela talet 570 och notera att det är jämnt och därför delbart med 2, vilket är ett primtal.
Vi kommer att använda ett snedstreck för att separera numret till vänster från delarna till höger. De respektive kvoterna placeras under det antal som de erhålls. Sönderdelningen är klar när den sista siffran i den vänstra kolumnen är 1:
570 │2
285 │
När man dividerar med 2 är kvoten 285 som är delbar med 5, ett annat primtal som slutar på 5.
570 │2
285 5
57 │
57 är delbart med 3, också ett primtal, eftersom summan av siffrorna 5 + 7 = 12 är en multipel av 3.
570 │2
285 5
57 3
19 │
Slutligen får vi 19, vilket är ett primtal, vars delare är 19 och 1:
570 │2
285 5
57 3
19-19
1 │
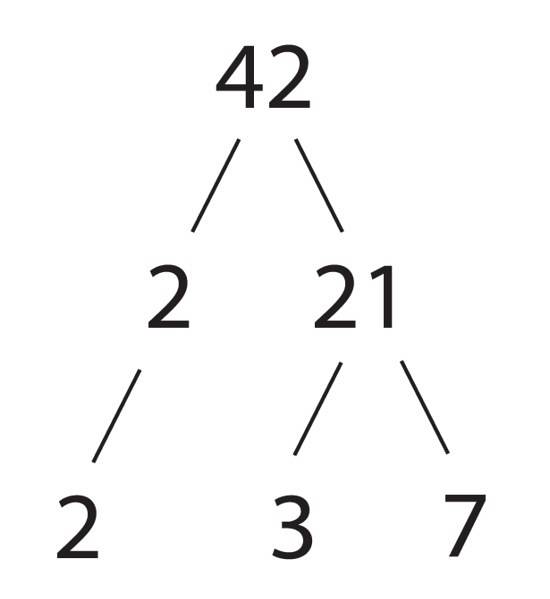
Genom att erhålla 1 kan vi redan uttrycka 570 på detta sätt:
570 = 2 x 5 x 3 x 19
Och vi ser att det i själva verket är en produkt av fyra primtal.
I det här exemplet börjar vi med att dela med 2, men samma faktorer (i en annan ordning) skulle ha uppnåtts om vi till exempel startade med att dela med 5.
Delbarhetskriterier
För att sönderdela ett sammansatt tal i dess primära faktorer är det nödvändigt att dela det exakt. Kriterierna för delbarhet mellan primtal är regler som gör det möjligt att veta när ett tal är delbart av en annan exakt, utan att behöva försöka eller bevisa.
-Delbarhet med 2
Alla jämna siffror, de som slutar på 0 eller ett jämnt antal är delbara med 2.
-Delbarhet med 3
Om summan av siffrorna i ett tal är en multipel av 3, så är antalet också delbart med 3.
-Delbarhet med 5
Siffror som slutar på 0 eller 5 är delbara med 5.
-Delbarhet med 7
Ett tal är delbart med 7 om det sista siffran separeras, multipliceras med 2 och det återstående talet subtraheras, blir det resulterande värdet en multipel av 7.
Denna regel verkar lite mer komplicerad än de tidigare, men i verkligheten är det inte så mycket, så låt oss titta på ett exempel: kommer 98 att delas med 7?
Låt oss följa instruktionerna: vi separerar den sista siffran som är 8, vi multiplicerar den med 2 som ger 16. Siffran som återstår när vi separerar 8 är 9. Vi subtraherar 16 - 9 = 7. Och eftersom 7 är en multipel av sig själv , 98 är delbart mellan 7.
-Delbarhet med 11
Om summan av siffrorna i jämnt läge (2, 4, 6 ...) subtraheras från summan av siffrorna i udda position (1, 3, 5, 7 ...) och 0 eller en multipel av 11 erhålls, erhålls talet är delbart med 11.
De första multiplarna av 11 kan lätt identifieras: de är 11, 22, 33, 44 ... 99. Men var försiktig, 111 är inte, istället är 110.
Som ett exempel, låt oss se om 143 är en multipel av 11.
Detta nummer har 3 siffror, den enda jämna siffran är 4 (den andra), de två udda siffrorna är 1 och 3 (första och tredje), och deras summa är 4.
Båda summorna subtraheras: 4 - 4 = 0 och eftersom 0 erhålls visar det sig att 143 är en multipel av 11.
-Delbarhet med 13
Numret utan en siffra måste subtraheras från 9 gånger den siffran. Om räkningen returnerar 0 eller en multipel av 13 är talet en multipel av 13.
Som ett exempel kommer vi att verifiera att 156 är en multipel av 13. Siffran är 6 och siffran som förblir utan den är 15. Vi multiplicerar 6 x 9 = 54 och nu subtraherar vi 54 - 15 = 39.
Men 39 är 3 x 13, så 56 är en multipel av 13.
Primera siffror till varandra
Två eller flera primtal eller sammansatta siffror kan vara primära eller samprima. Det betyder att den enda gemensamma delaren de har är 1.
Det finns två viktiga egenskaper att komma ihåg när det gäller coprimes:
-Två, tre och fler nummer i följd är alltid primära för varandra.
-Samma sak kan sägas för två, tre eller flera udda siffror i rad.
Till exempel 15, 16 och 17 är primtal för varandra och så är 15, 17 och 19.
Hur vet jag hur många delare ett sammansatt tal har
Ett primtal har två delare, samma nummer och 1. Och hur många delare har ett sammansatt tal? Dessa kan vara kusiner eller föreningar.
Låt N vara ett sammansatt tal uttryckt i termer av dess kanoniska sönderdelning enligt följande:
N = an . bm. csid... rk
Där a, b, c ... r är huvudfaktorerna och n, m, p ... k respektive exponenter. Tja, antalet delare C som N har ges av:
C = (n +1) (m + 1) (p +1) ... (k + 1)
Med C = primordelare + sammansatta delare + 1
Till exempel 570, som uttrycks så här:
570 = 2 x 5 x 3 x 19
Alla huvudfaktorer höjs till 1, därför har 570:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 delare
Av dessa 10 delare vet vi redan: 1, 2, 3, 5, 19 och 570. Det finns ytterligare 10 delare som är sammansatta tal: 6, 10, 15, 30, 38, 57, 95, 114, 190 och 285. De hittas genom att observera nedbrytningen i primära faktorer och också multiplicera kombinationer av dessa faktorer tillsammans..
Lösta övningar
- Övning 1
Sönderdela följande siffror i huvudfaktorer:
a) 98
b) 143
c) 540
d) 3705
Lösning till
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
Lösning b
143 11
13-13
1 │
143 = 11 x 13
Lösning c
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2två x 33
Lösning d
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
- Övning 2
Ta reda på om följande siffror är primära för varandra:
6, 14, 9
Lösning
-Delarna av 6 är: 1, 2, 3, 6
-När det gäller de 14 är den delbar med: 1, 2, 7, 14
-Slutligen har 9 som delare: 1, 3, 9
Den enda delaren de har gemensamt är 1, därför är de primära för varandra.
Referenser
- Baldor, A. 1986. Aritmetik. Codex-utgåvor och distributioner.
- Byju's. Primera och sammansatta siffror. Återställd från: byjus.com.
- Primera och sammansatta siffror. Återställd från: profeyennyvivaslapresentacion.files.wordpress.com
- Smartick. Delbarhetskriterier. Återställd från: smartick.es.
- Wikipedia. Sammansatta siffror. Återställd från: en.wikipedia.org.


Ingen har kommenterat den här artikeln än.