Perfekta siffror för hur man identifierar dem och exempel

A perfekt nummer är ett naturligt tal så att summan av dess delare är samma som antalet. Självklart kan själva numret inte inkluderas mellan delarna.

Ett av de enklaste exemplen på ett perfekt tal är 6, eftersom dess delare är: 1, 2 och 3. Om vi ​​lägger till delarna får vi: 1 + 2 + 3 = 6.

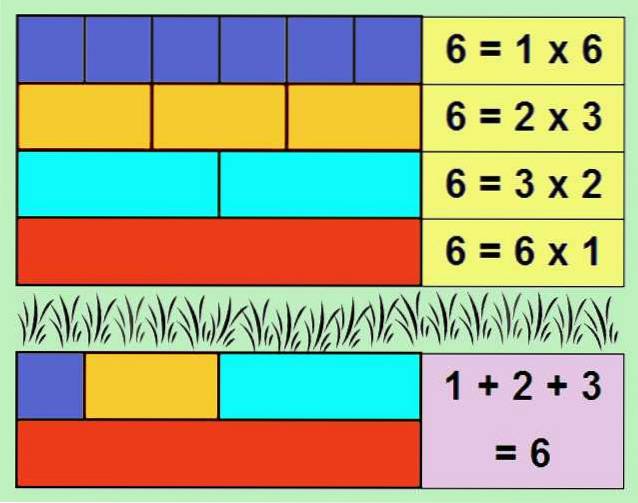
Summan av delarna av ett heltal, exklusive själva numret, kallas alikvot. Därför är ett perfekt antal lika med dess alikvot.

Men om själva numret ingår i summan av delarna av ett tal, kommer ett perfekt tal att vara ett som summan av alla dess delare dividerat med 2 är lika med själva numret..

Artikelindex

• 1 Historia
• 2 Egenskaper för perfekta siffror
  • 2.1 Euclids formel och kriterium
  • 2.2 Det största kända perfekta numret
  • 2.3 Ett perfekt nummer är vänner med sig själv
• 3 Exempel på perfekta siffror
• 4 Övningar
  • 4.1 - Övning 1
  • 4.2 - Övning 2
  • 4.3 - Övning 3
  • 4.4 - Övning 4
• 5 Referenser

Berättelse

Antikens matematiker, särskilt grekerna, fäste stor vikt vid perfekta tal och tilldelade dem gudomliga kvaliteter..

Till exempel bekräftade Philo av Alexandria mot det första århundradet att 6 och 28 är perfekta siffror som sammanfaller med de sex dagar som skapades av världen och de tjugoåtta dagar som det tar för månen att gå runt jorden..

Perfekta siffror finns också i naturen, till exempel vid nordpolen i Saturnus visas också det perfekta talet 6, en sexkantig virvel som hittades av Cassini-sonden och som forskare har fascinerat.. 

Bin av bikakor har celler i sexkantig form, det vill säga med 6 sidor. Det har visats att polygonen med det perfekta talet 6 är det som gör det möjligt att maximera antalet celler i bikupan, med ett minimum av vax för dess utarbetande..

Egenskaper för perfekta siffror

Summan av alla delare av ett naturligt tal n betecknas med σ (n). I ett perfekt tal är det nöjd med att: σ (n) = 2n.

Euclids formel och kriterier

Euclid upptäckte en formel och ett kriterium som gör det möjligt att hitta de perfekta siffrorna. Denna formel är:

två^(n-1) (tvåⁿ -1)

Antalet som genereras av formeln är dock perfekt endast när faktorn (2ⁿ -1) vara kusin.

Låt oss se hur de första perfekta siffrorna genereras:

Om n = 2 är vi kvar med 2¹ (två^två - 1) = 2 x 3 = 6 som vi redan såg är perfekt.

När n = 3 har vi 2^två (två³ - 1) = 4 x 7 = 28 vilket också är perfekt, såsom verifierat i detalj i exempel 1.

Låt oss se vad som händer med n = 4. När vi ersätter i Euclids formel har vi:

två³ (två⁴ - 1) = 8 x 15 = 120

Det kan verifieras att detta tal inte är perfekt, vilket visas i detalj i exempel 3. Detta strider inte mot Euclids kriterium, eftersom 15 inte är primärt, ett nödvändigt krav för att resultatet ska vara ett perfekt antal.

Låt oss nu se vad som händer när n = 5. Tillämpa formeln vi har:

två⁴ (två⁵ - 1) = 16 x 31 = 496

Eftersom 31 är ett primtal, måste talet 496 vara perfekt, enligt Euclids kriterier. I exempel 4 visas det i detalj att det verkligen är.

Primtal som har formen 2^sid - 1 kallas Mersenne-kusiner, efter munken Marin Mersenne, som studerade primtal och perfekta siffror redan på 1600-talet..

Senare på 1700-talet visade Leonhard Euler att alla perfekta siffror genererade av Euclids formel är jämna.

Hittills har ingen perfekt hittats som är udda.

Det största kända perfekta numret

Hittills är 51 perfekta nummer kända, alla genererade med formeln och Euclids kriterium. Detta nummer erhölls när den större Mersenne-kusinen hittades, vilket är: (2^82589933 - 1).

Det perfekta nummer # 51 är (2^82589933) x (2^82589933 - 1) och har 49724095 siffror.

Ett perfekt nummer är vänner med sig själv

I talteori sägs det att två nummer är vänner när summan av delarna av en, inte själva numret, är lika med det andra numret och vice versa.

Läsaren kan verifiera att summan av delarna av 220, exklusive 220 är 284. Å andra sidan är summan av delarna av 284, inklusive 284, lika med 220. Därför är antalet siffror 220 och 284 vänner.

Ur denna synvinkel är ett perfekt antal vänner med sig själv..

Exempel på perfekta siffror

De första åtta perfekta siffrorna listas nedan:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Träning

I följande övningar kommer det att bli nödvändigt att beräkna delarna för ett tal, sedan lägga till dem och verifiera om numret är ett perfekt tal eller inte..

Innan vi närmar oss övningarna kommer vi därför att granska konceptet och visa hur de beräknas..

Till att börja med måste du komma ihåg att siffrorna kan vara primära (när de bara kan delas exakt med sig själv och 1) eller sammansatta (när de kan sönderdelas som en produkt av primtal).

För ett sammansatt tal N har vi:

N = aⁿ . b^m. c^sid ... r^k 

Där a, b, c ... r är primtal och n, m, p ... k är exponenter som tillhör de naturliga talen, som kan vara från 1 och framåt.

När det gäller dessa exponenter finns det en formel för att veta hur många delare talet N har, även om det inte säger oss vad det är. Låt C vara denna kvantitet, sedan:

C = (n +1) (m + 1) (p +1) ... (k + 1)

Att sönderdela talet N som en produkt av primtal och att veta hur många delare det har, både primt och icke-primt, hjälper oss att bestämma vad dessa delare är..

När du har alla, utom den sista som inte krävs i summan, kan du kontrollera om det är ett perfekt nummer eller inte.

- Övning 1

Kontrollera att siffran 28 är perfekt.

Lösning

Det första kommer att vara att sönderdela numret i dess primära faktorer.

28 | 2
14 | 2
07 | 7
01 | 1

Delarna är: 1, 2, 4, 7, 14 och 28. Om vi ​​utesluter 28 ger summan av delarna:

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Därför är 28 ett perfekt nummer.

Dessutom är summan av alla dess delare 28 + 28 så regeln σ (28) = 2 x 28 uppfylls.

- Övning 2

Beslutar om siffran 38 är perfekt eller inte.

Lösning

Talet sönderdelas i dess främsta faktorer:

39 | 3
13 | 13
01 | 1

Delarna av 39 utan att inkludera själva numret är: 1, 3 och 13. Summan 1 + 3 + 13 = 4 + 13 = 17 är inte lika med 39, därför är 39 ett ofullkomligt eller icke-perfekt tal. 

- Övning 3

Ta reda på om nummer 120 är perfekt eller ofullständigt.

Lösning

Vi fortsätter att sönderdela numret i dess främsta faktorer:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Från de främsta faktorerna fortsätter vi med att hitta delarna:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 och 120

Om 120 var perfekta, skulle lägga till alla dess delare få 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Detta resultat skiljer sig klart från 240, så det dras slutsatsen att siffran 120 inte är ett perfekt nummer..

- Övning 4

Kontrollera att siffran 496, erhållen enligt Euclids kriterium, är ett perfekt nummer.

Lösning

Talet 496 sönderdelas i dess huvudfaktorer:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Så dess delare är:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Nu läggs alla till, förutom 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Bekräftar att det verkligen är ett perfekt nummer.

Referenser

1. Baldor, A. 1986. Aritmetik. Codex-utgåvor och distributioner.
2. Allt om primtal. Vänliga nummer. Återställd från: numeroprimos.org.
3. Wolfram MathWorld. Eulers regel. Återställd från: mathworld.wolfram.com.
4. Wolfram MathWorld. Perfekt nummer. Återställd från: mathworld.wolfram.com.
5. Wikipedia. Perfekta siffror. Återställd från: en.wikipedia.org.
6. Wikipedia. Vänliga nummer. Återställd från: es.wikipedia.org.