
Verkliga siffror historia, exempel, egenskaper, operationer

De riktiga nummer de utgör den numeriska uppsättningen som inkluderar de naturliga tal, heltal, det rationella och det irrationella. De betecknas med symbolen ℝ eller helt enkelt R och omfattningen inom vetenskap, teknik och ekonomi är sådan att när man talar om "antal", är det nästan givet för givet att det är ett verkligt antal.
Verkliga siffror har använts sedan urminnes tider, även om de inte fick det namnet. Redan från den tid då Pythagoras utvecklade sin berömda sats uppstod siffror som inte kunde erhållas som kvoter av naturliga tal eller heltal.
Exempel på siffror är √2, √3 och π. Dessa nummer kallas irrationell, i motsats till rationella tal, som kommer från heltal. Det var därför nödvändigt med en numerisk uppsättning som omfattar båda klasserna av siffror..
Uttrycket "riktigt tal" skapades av den stora matematikern René Descartes (1596-1650) för att skilja mellan de två typerna av rötter som kan uppstå genom att lösa en polynomekvation.
Några av dessa rötter kan till och med vara rötter av negativa tal, Descartes kallade dessa "imaginära tal" och de som inte var, var verkliga tal.
Benämningen kvarstod över tiden och gav upphov till två stora numeriska uppsättningar: reella tal och komplexa siffror, en större uppsättning som inkluderar reella tal, imaginära tal och de som är delverkliga och delvis imaginära..
Utvecklingen av reella tal fortsatte sin kurs tills 1872, matematikern Richard Dedekind (1831-1936) definierade formellt uppsättningen av reella tal genom den så kallade skär av Dedekind. Syntesen av hans arbete publicerades i en artikel som såg ljuset samma år.
Artikelindex
- 1 Exempel på reella tal
- 1.1 Representation av reella tal på den verkliga linjen
- 2 Egenskaper för reella tal
- 3 Operationer med verkliga siffror
- 4 applikationer
- 5 Övningen löst
- 5.1 Övning 1
- 6 Referenser
Exempel på verkliga siffror
Tabellen nedan visar exempel på reella tal. Denna uppsättning har som delmängder de naturliga siffrorna, heltal, det rationella och det irrationella. Varje antal av dessa uppsättningar är i sig ett verkligt antal.
Därför är 0, negativa, positiva, bråk och decimaler reella tal.

Representation av reella tal på den verkliga linjen
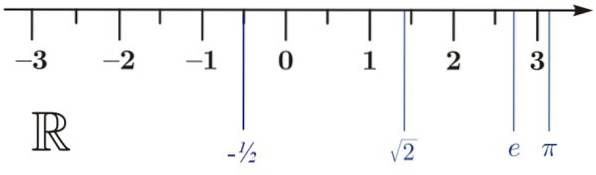
Verkliga siffror kan representeras på den verkliga raden R, som bilden visar. Det är inte nödvändigt att 0 alltid är närvarande, men det är bekvämt att veta att till vänster finns de negativa realerna och till höger de positiva. Det är därför det är en utmärkt referenspunkt.
På den verkliga linjen tas en skala där heltalen hittas:… 3, -2, -1, 1, 2, 3…. Pilen indikerar att linjen sträcker sig till oändlighet. Men det är inte allt, i något betraktat intervall kommer vi också alltid att hitta oändliga reella tal.
De verkliga siffrorna representeras i ordning. Till att börja med finns det ordningen på heltal, där positiva alltid är större än 0, medan negativ är mindre..
Denna ordning hålls inom de verkliga siffrorna. Följande ojämlikheter visas som ett exempel:
a) -1/2 < √2
b) e < π
c) π> -1/2
Egenskaper för reella tal
-Verkliga tal inkluderar naturliga tal, heltal, rationella tal och irrationella tal..
-Den kommutativa egenskapen för tillägget uppfylls: tilläggsordningen ändrar inte summan. Om a och b är två reella tal är det alltid sant att:
a + b = b + a
-0 är det neutrala elementet i summan: a + 0 = a
-För summan uppfylls den associerade egenskapen. Om a, b och c är reella tal: (a + b) + c = a + (b + c).
-Motsatsen till ett reellt tal är -a.
-Subtraktion definieras som summan av det motsatta: a - b = a + (-b).
-Produktens kommutativa egenskap uppfylls: Faktornas ordning förändrar inte produkten: a.b = b.a
-I produkten tillämpas även den associerande egenskapen: (a.b) .c = a. (B.c)
-1 är det neutrala elementet i multiplikationen: a.1 = a
-Den fördelande egenskapen för multiplikation med avseende på addition är giltig: a. (b + c) = a.b + a.c
-Division med 0 är odefinierad.
-Varje reellt tal a, utom 0, har ett multiplikativ invers av-1 så att a.a-1 = 1.
-Om a är ett verkligt tal: a0 = 1 och a1 = a.
-Det absoluta värdet eller modulen för ett reellt tal är avståndet mellan nämnda tal och 0.
Operationer med verkliga siffror
Med de verkliga siffrorna kan du utföra de operationer som görs med andra numeriska uppsättningar, inklusive addition, subtraktion, multiplikation, division, empowerment, radication, logaritmer och mer.
Som alltid är delning med 0 inte definierad, inte heller negativa logaritmer av tal eller 0, även om det är sant att log 1 = 0 och att logaritmer av tal mellan 0 och 1 är negativa.
Applikationer
Tillämpningen av verkliga siffror på alla typer av situationer är extremt varierad. Verkliga siffror visas som svar på många problem inom exakt vetenskap, datavetenskap, teknik, ekonomi och samhällsvetenskap..
Alla typer av storheter och kvantiteter som avstånd, tider, krafter, ljudintensitet, pengar och många fler har sitt uttryck i reella tal.
Överföring av telefonsignaler, bild och ljud från en video, temperaturen på en luftkonditionering, en värmare eller ett kylskåp kan styras digitalt, vilket innebär att fysiska kvantiteter omvandlas till numeriska sekvenser.
Detsamma händer när du gör en banktransaktion via Internet eller konsulterar snabbmeddelanden. De verkliga siffrorna finns överallt.
Övningen löst
Vi kommer att se med övningar hur dessa siffror fungerar i vanliga situationer som vi möter dagligen..
Övning 1
Postkontoret accepterar endast paket för vilka längden, plus omkretsmätningen, inte överstiger 108 tum. För att det visade paketet ska accepteras måste det därför uppfyllas att:
L + 2 (x + y) ≤ 108
a) Kommer ett paket som mäter 6 tum brett, 8 tum högt och 5 fot långt igenom??
b) Vad sägs om en som mäter 2 x 2 x 4 fot3?
c) Vad är den högsta acceptabla höjden för ett paket vars bas är kvadratisk och mäter 9 x 9 tumtvå?
Svara på
L = 5 fot = 60 tum
x = 6 tum
y = 8 tum
Åtgärden att lösa är:
L + 2 (x + y) = 60 + 2 (6 + 8) tum = 60 + 2 x 14 tum = 60 + 28 tum = 88 tum
Paketet accepteras.
Svar b
Måtten på detta paket är mindre än paket a), så de lyckas båda passera.
Svar c
I detta paket:
x = L = 9 tum
Det måste uppfyllas att:
9+ 2 (9 + y) ≤ 108
27 + 2y ≤ 108
2y ≤ 81
och ≤ 40,5 tum
Referenser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Diego, A. Verkliga siffror och deras egenskaper. Återställd från: matematica.uns.edu.ar.
- Figuera, J. 2000. Matematik 9: e. Kvalitet. CO-BO-utgåvor.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Matematik för Calculus. 5: e. Utgåva. Cengage Learning.



Ingen har kommenterat den här artikeln än.