
Hyperbolisk paraboloid definition, egenskaper och exempel

A hyperbol paraboloid är en yta vars allmänna ekvation i kartesiska koordinater (x, y, z) uppfyller följande ekvation:
(för)två - (och / b)två - z = 0.
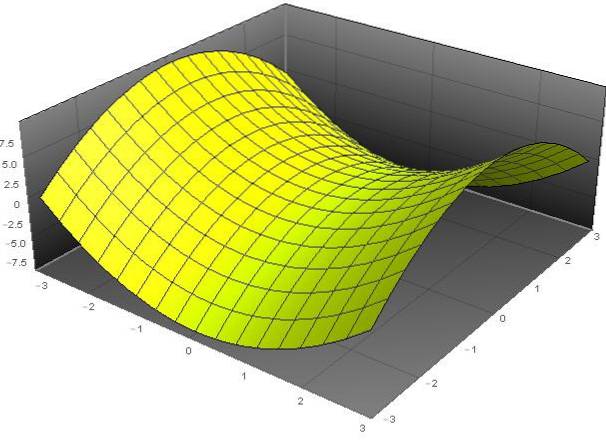
Namnet "paraboloid" kommer från det faktum att variabeln z beror på kvadraterna för variablerna x och y. Medan adjektivet "hyperboliskt" beror på det faktum att vid fasta värden på z har vi ekvationen av en hyperbol. Formen på denna yta liknar en hästsadel.
Artikelindex
- 1 Beskrivning av den hyperboliska paraboloid
- 2 Egenskaper hos den hyperboliska paraboloid
- 3 Arbetade exempel
- 3.1 - Exempel 1
- 3.2 - Exempel 2
- 3.3 - Exempel 3
- 4 Den hyperboliska paraboloid i arkitektur
- 5 Referenser
Beskrivning av den hyperboliska paraboloid
För att förstå den hyperboliska paraboloidens natur kommer följande analys att göras:
1.- Vi tar det specifika fallet a = 1, b = 1, det vill säga den kartesiska ekvationen av paraboloid förblir som z = xtvå - Ytvå.
2.- Plan som är parallella med ZX-planet betraktas, det vill säga y = ctte.
3.- Med y = ctte förblir det z = xtvå - C, som representerar parabolor med grenar upp och toppar under XY-planet.
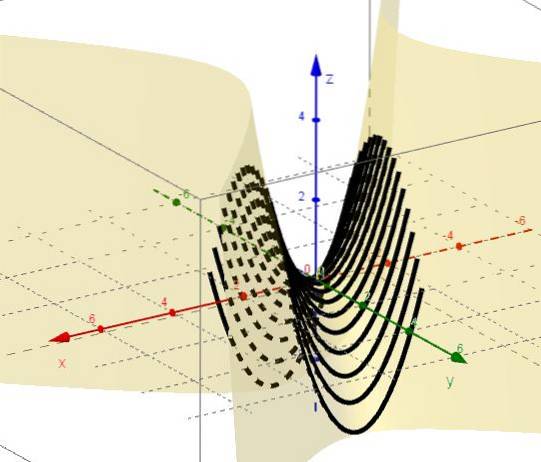
4.- Med x = ctte förblir det z = C - ytvå, som representerar parabolor med grenar ner och toppar ovanför XY-planet.
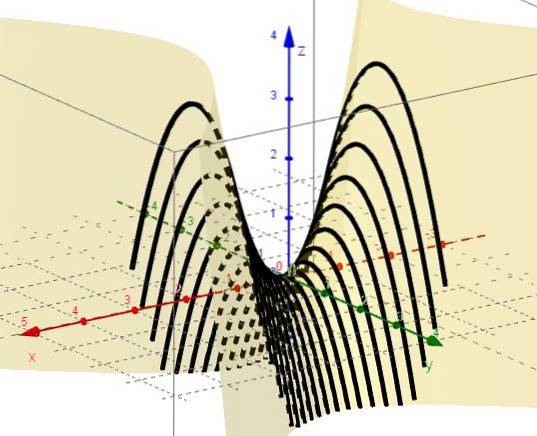
5.- Med z = ctte förblir det C = xtvå - Ytvå, som representerar hyperboler i plan parallellt med XY-planet. När C = 0 finns två linjer (vid + 45 ° och -45 ° i förhållande till X-axeln) som skär varandra vid ursprunget på XY-planet.
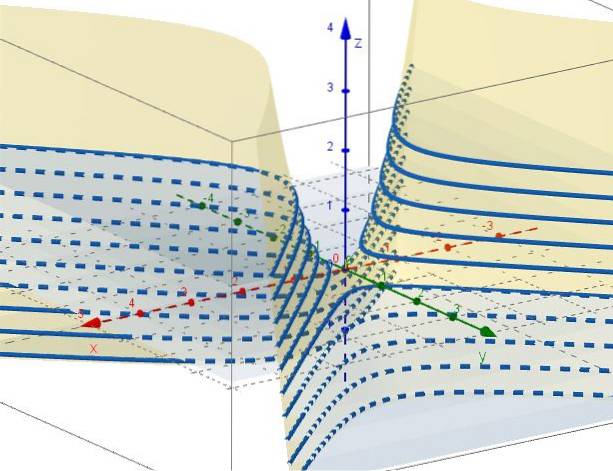
Egenskaper hos den hyperboliska paraboloid
1. - Fyra olika punkter i tredimensionellt utrymme definierar en och endast en hyperbol paraboloid.
2.- Den hyperboliska paraboloid är en dubbelt reglerad yta. Detta innebär att trots att det är en böjd yta, passerar två olika linjer genom varje punkt i en hyperbol paraboloid som helt tillhör den hyperboliska paraboloid. Den andra ytan som inte är ett plan och är dubbelt styrd är revolutionens hyperboloid.
Det är just den andra egenskapen hos den hyperboliska paraboloid som har gjort det möjligt att använda den i arkitektur eftersom ytan kan genereras från balkar eller raka rep..
Den andra egenskapen hos den hyperboliska paraboloid tillåter en alternativ definition av den: är ytan som kan genereras av en rörlig rak linje parallellt med ett fast plan och skär två fasta linjer som fungerar som en guide. Följande figur klargör denna alternativa definition av hyperbolisk paraboloid:
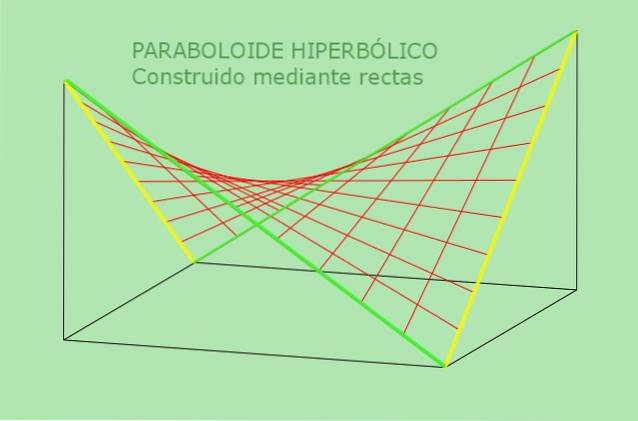
Arbetade exempel
- Exempel 1
Visa att ekvationen: z = xy, motsvarar en hyperbol paraboloid.
Lösning
En transformation kommer att tillämpas på variablerna x och y motsvarande en rotation av de kartesiska axlarna i förhållande till Z-axeln + 45º. De gamla x- och y-koordinaterna omvandlas till de nya x 'och y' enligt följande relationer:
x = x '- y'
y = x '+ y'
medan z-koordinaten förblir densamma, det vill säga z = z '.
Genom att ersätta ekvationen z = x och vi har:
z '= (x' - y ') (x' + y ')
Genom att tillämpa den anmärkningsvärda produkten av skillnaden med summan lika med skillnaden i kvadrater har vi:
z '= x'två - Y 'två
vilket tydligt motsvarar den ursprungligen givna definitionen av hyperbol paraboloid.
Avlyssningen av planen parallellt med XY-axeln med den hyperboliska paraboloid z = x och bestämmer liksidiga hyperboler som har asymptoter på planen x = 0 och y = 0.
- Exempel 2
Bestäm parametrarna till Y b av den hyperboliska paraboloid som passerar genom punkterna A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) och D (2, -1, 32/9).
Lösning
Enligt dess egenskaper bestämmer fyra punkter i tredimensionellt utrymme en enda hyperbol paraboloid. Den allmänna ekvationen är:
z = (x / a)två - (och / b)två
Vi ersätter de angivna värdena:
För punkt A har vi 0 = (0 / a)två - (0 / b)två, ekvation som uppfylls oavsett värdena för parametrarna a och b.
Genom att ersätta punkt B får vi:
5/9 = 1 / atvå - 1 Btvå
Medan det för punkt C kvarstår:
32/9 = 4 / atvå - 1 Btvå
Slutligen, för punkt D får vi:
32/9 = 4 / atvå - 1 Btvå
Vilket är identiskt med föregående ekvation. I slutändan måste ekvationssystemet lösas:
5/9 = 1 / atvå - 1 Btvå
32/9 = 4 / atvå - 1 Btvå
Att subtrahera den andra ekvationen från den första ger:
27/9 = 3 / atvå vilket innebär att entvå = 1.
På samma sätt subtraheras den andra ekvationen från fyrdubbel av den första, vilket ger:
(32-20) / 9 = 4 / atvå - 4 / atvå -1 Btvå + 4 / btvå
Vilket är förenklat som:
12/9 = 3 / btvå ⇒ btvå = 9/4.
Kort sagt, den hyperboliska paraboloid som passerar genom de givna punkterna A, B, C och D har en kartesisk ekvation som ges av:
z = xtvå - (4/9) ochtvå
- Exempel 3
Enligt egenskaperna hos den hyperboliska paraboloid passerar två linjer genom varje punkt som är helt inneslutna i den. För fallet z = x ^ 2 - y ^ 2 hitta ekvationen för de två linjerna som passerar genom punkten P (0, 1, -1) som tydligt tillhör den hyperboliska paraboloid, så att alla punkterna i dessa linjer också tillhör till samma sak.
Lösning
Med hjälp av den anmärkningsvärda produkten av skillnaden i kvadrater kan ekvationen för den hyperboliska paraboloid skrivas så här:
(x + y) (x - y) = c z (1 / c)
Där c är en icke-noll konstant.
Ekvationen x + y = c z och ekvationen x - y = 1 / c motsvarar två plan med normala vektorer n=<1,1,-c> Y m=<1,-1,0>. Vektorprodukten m x n =<-c, -c, -2> ger oss riktningen för skärningslinjen mellan de två planen. Sedan har en av raderna som passerar genom punkten P och tillhör den hyperboliska paraboloid en parametrisk ekvation:
För att bestämma c ersätter vi punkten P i ekvationen x + y = c z och erhåller:
c = -1
På liknande sätt, men med tanke på ekvationerna (x - y = k z) och (x + y = 1 / k) har vi linjens parametriska ekvation:
Sammanfattningsvis de två raderna:
De ingår helt i den hyperboliska paraboloid z = xtvå - Ytvå passerar genom punkten (0, 1, -1).
Antag som en kontroll, t = 1 som ger oss punkten (1,2, -3) på första raden. Du måste kontrollera om det också finns på paraboloid z = xtvå - Ytvå:
-3 = 1två - tvåtvå = 1 - 4 = -3
Vilket bekräftar att det verkligen tillhör ytan av den hyperboliska paraboloid.
Den hyperboliska paraboloid i arkitektur

Den hyperboliska paraboloid har använts i arkitekturen av de stora avantgardearkitekterna, bland vilka namnen på den spanska arkitekten Antoni Gaudí (1852-1926) och särskilt den även spanska Félix Candela (1910-1997) sticker ut..
Nedan följer några verk baserade på den hyperboliska paraboloid:
-Kapell i staden Cuernavaca (Mexiko) arbete av arkitekten Félix Candela.
-The Oceanographic of Valencia (Spanien), också av Félix Candela.
Referenser
- Encyklopedi av matematik. Reglerad yta. Återställd från: encyclopediaofmath.org
- Llera Rubén. Hyperbol paraboloid. Återställd från: rubenllera.wordpress.com
- Weisstein, Eric W. "Hyperbolisk paraboloid." Från MathWorld-A Wolfram Web Resource. Återställd från: mathworld.wolfram.com
- Wikipedia. Paraboloid. Återställd från: en.wikipedia.com
- Wikipedia. Paraboloid. Återställd från: es.wikipedia.com
- Wikipedia. Reglerad yta. Återställd från: en.wikipedia.com


Ingen har kommenterat den här artikeln än.