De statistisk population Det är den kollektiva eller kompletta uppsättningen element med gemensamma egenskaper och som du vill studera. Dessa element kan vara människor, levande varelser, livlösa föremål, händelser, attityder till en händelse och olika företag..
Exempel på befolkningar är invånarna i ett helt land eller en stad, artiklarna som produceras av en fabrik efter en dag eller antalet stjärnor i Vintergatan. På samma sätt kan alla betyg som erhållits av studenter vid ett universitet i slutet av skolperioden klassificeras som en statistisk population.
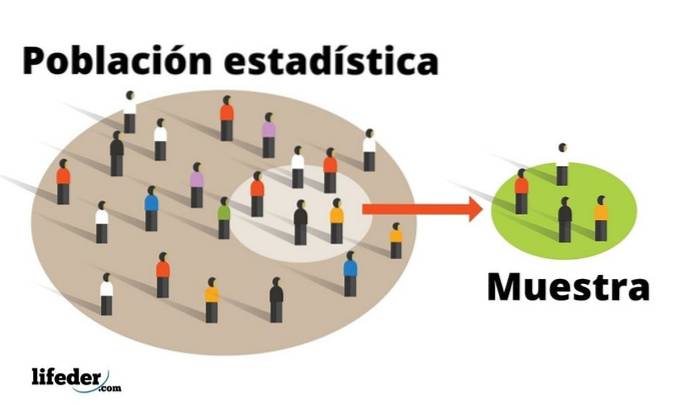
Forskaren är den som bestämmer vilka egenskaper som är intressanta hos den befolkning som ska studeras. Av denna anledning, eftersom utbudet av möjligheter är så brett, klassificeras populationer av några enastående egenskaper, såsom deras storlek..
Detta avgör det vanligaste sättet att klassificera statistiska populationer, så att befolkningar i allmänhet sägs vara oändliga eller ändliga. Det finns dock också andra distinkta attribut, alltid ur forskningen som ska genomföras..
Sådana attribut definieras i förväg för att säkerställa att de uppfyller studiens krav och samtidigt hjälper forskaren att ge befolkningen lämplig behandling..
Befolkningar studeras vanligtvis genom ett noggrant utvalt urval: detta är en representativ delmängd, vars mindre storlek gör det lättare att hantera. I förlängningen motsvarar urvalets egenskaper de i befolkningen inom en smal marginal, vilket forskaren på ett bekvämt sätt använder statistiska tekniker..
I princip kan det finnas så många typer av statistiska populationer som det finns egenskaper som ska ingå i deras definition, men det finns några kriterier som de flesta forskare använder för att klassificera dem och som är allmänt tillämpliga..
Det bör också noteras att vissa populationer passar sömlöst med mer än en kategori som anges nedan:
De är teoretiska populationer, eftersom de innehåller en oändlig mängd element. Vissa befolkningar har dock så många element att de i praktiken anses vara oändliga eftersom summan är mycket svår att bestämma..
-Uppsättningen av verkliga siffror.
-Antal syreatomer i luften i ett rum.
De har ett begränsat antal komponenter, och deras antal kan vara ganska stort eller tvärtom litet.
-Antalet anställda i ett företag.
-Totalt antal studenter i ett land.
Det hänvisar till en grupp av element vars existens är väsentlig eller också till konkreta observationer om någon händelse.
-Det totala antalet blåvalar som finns.
-Konsumenternas attityd till en ny produkt på marknaden.
I denna kategori finns observationer om potentiella händelser och även psykologiska egenskaper.
-Ångestnivåerna hos en grupp människor före risken för en katastrof.
Dessa är populationer vars egenskaper bibehålls i tid och rum eller inte varierar signifikant.
-Rotationsperioden för planeterna.
För sin del har instabila populationer en eller flera variabla egenskaper, både i tid och rum..
-Mängden människor i en stad som konsumerar ett visst läsk är ett exempel på en instabil befolkning, eftersom preferenser kan förändras på kort sikt om en annan produkt med mer slående egenskaper visas (ett konkurrerande varumärke som säljs eller att det presenteras med en ny färg eller smak ...).
De är kopplade till en eller flera egenskaper och kan därför variera när de ändras, helt eller delvis..
-Försäljning av produkter med populationer som bland annat beror på investeringen i reklam.
I denna befolkning försöker vi bestämma förekomsten eller frånvaron av en viss egenskap.
-I studier om kemi av mineralvatten för konsumtion är det vanligt att indikera närvaron av någon förening, såsom natriumklorid eller kalciumkarbonat.
I polynompopulationer är det avsett att utföra mätningen av en uppsättning egenskaper.
-Ålder, längd och vikt för elever i en grundskola.
I dessa populationer finns förändringar på grund av slump eller omständigheter utanför mänsklig kontroll.
-Det finns industriella processer där oförutsedda variationer påverkar kvaliteten på slutprodukterna. Om det fanns strömavbrott under en vecka med åskväder, vilket påverkade en kartongfabrik, kanske produktionen av den veckan inte är av samma kvalitet som den vanliga produktionen.
Nedan följer en illustrativ lista över populationer av olika typer som kan förekomma i många områden. Det är viktigt att betona igen att samma befolkning kan tillhöra mer än en av de beskrivna typerna, eftersom den har egenskaper gemensamt med dem..
- Den totala kattpopulationen i ett land (verklig och oändlig befolkning).
- Vattenmolekyler i Atlanten (det är en riktig och oändlig befolkning, eftersom den innehåller en sådan mängd element att det i praktiken är omöjligt att totalisera dem).
- Alla virus som finns på jorden (verklig och oändlig befolkning).
- Antal för tidigt födda under nästa trimester (hypotetisk population, eftersom födslarna ännu inte har inträffat, och det också är ändligt).
- Antal djur som drabbats av nästa möjliga skogsbrand under nästa torrsäsong (hypotetisk och begränsad population).
- Antal stjärnor i kärnan av Vintergatan (ändlig och stabil befolkning, eftersom antalet stjärnor förblir konstant under lång tid och också är verkligt).
-Uppsättningen av alla primtal (oändlig, stabil och verklig befolkning).
- Kolesterolnivåer i befolkningen i EU-länderna (ändlig, beroende, verklig, instabil befolkning).
- Antal överlevande i händelse av Vesuv-utbrott (hypotetisk befolkning, ändlig, instabil).
Ingen har kommenterat den här artikeln än.