Heptagonala prismaegenskaper, volym, area

A heptagonalt prisma Det är en geometrisk figur som, som namnet antyder, innefattar två geometriska definitioner som är: prisma och heptagon. Ett "prisma" är en geometrisk figur som är begränsad av två baser som är lika och parallella polygoner och deras sidoytor är parallellogram..

En "heptagon" är en polygon som består av sju (7) sidor. Eftersom en heptagon är en polygon kan den vara regelbunden eller oregelbunden.

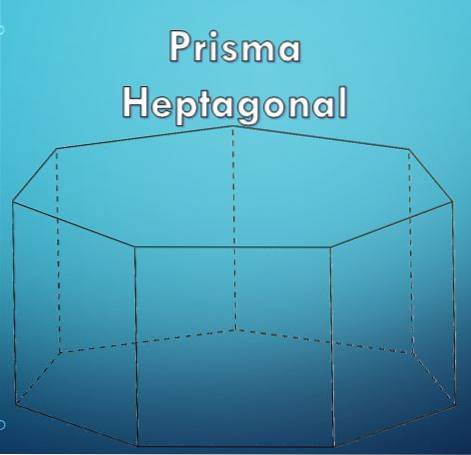
En polygon sägs vara regelbunden om alla sidor har samma längd och dess inre vinklar mäter samma, de kallas också liksidiga polygoner; annars sägs polygonen vara oregelbunden.

Kännetecken för ett heptagonalt prisma

Nedan följer vissa egenskaper som ett heptagonalt prisma har, såsom: dess konstruktion, dess basegenskaper, ytan på alla ansikten och dess volym..

1- Konstruktion

För att bygga ett heptagonalt prisma är två heptagoner nödvändiga, vilka kommer att vara dess baser och sju parallellogram, en för varje sida av heptagon..

Du börjar med att rita en heptagon, sedan dras sju vertikala linjer, av lika längd, som kommer ut från var och en av dess hörn.

Slutligen ritas en annan heptagon så att dess hörn sammanfaller med slutet av de linjer som ritades i föregående steg..

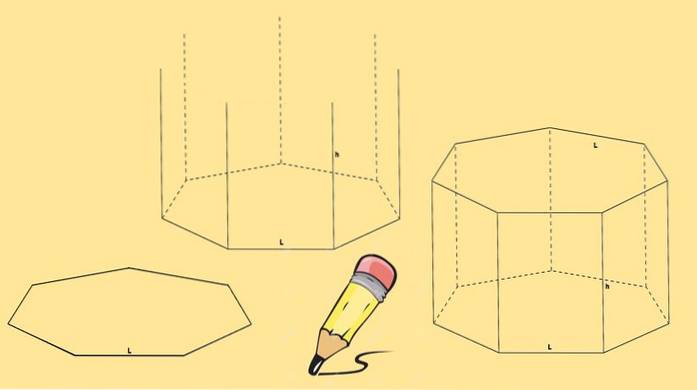
Det heptagonala prisma som dras ovan kallas ett rätt heptagonalt prisma. Men du kan också ha ett snett heptagonalt prisma som det i följande figur.

2- Egenskaper hos dess baser

Eftersom dess baser är heptagoner uppfyller de att det diagonala talet är D = nx (n-3) / 2, där "n" är antalet sidor av polygonen; i det här fallet har vi D = 7 × 4/2 = 14.

Vi kan också se att summan av de inre vinklarna för vilken som helst heptagon (vanlig eller oregelbunden) är lika med 900º. Detta kan verifieras med följande bild.

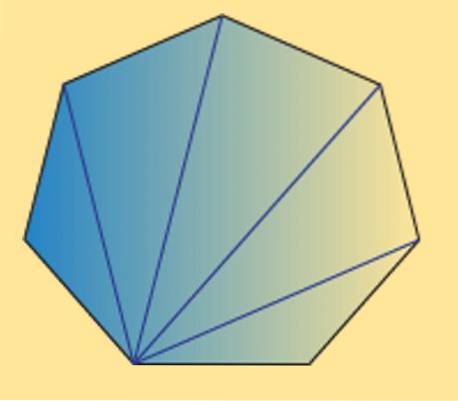
Som framgår finns det 5 inre trianglar, och med hjälp av att summan av de inre vinklarna i en triangel är lika med 180 ° kan det erhållas att önskat resultat.

3- Område behövs för att bygga ett heptagonalt prisma

Eftersom baserna är två heptagoner och dess sidor är sju parallellogram, är det område som behövs för att bygga ett heptagonalt prisma lika med 2xH + 7xP, där "H" är området för varje heptagon och "P" är varje parallellogram..

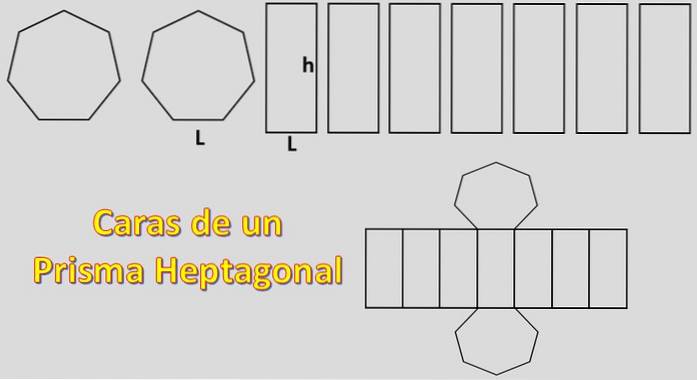
I detta fall beräknas arean för en vanlig heptagon. För detta är det viktigt att känna till definitionen av apotem.

Apotemet är en vinkelrät linje som går från mitten av en vanlig polygon till mittpunkten på någon av dess sidor.

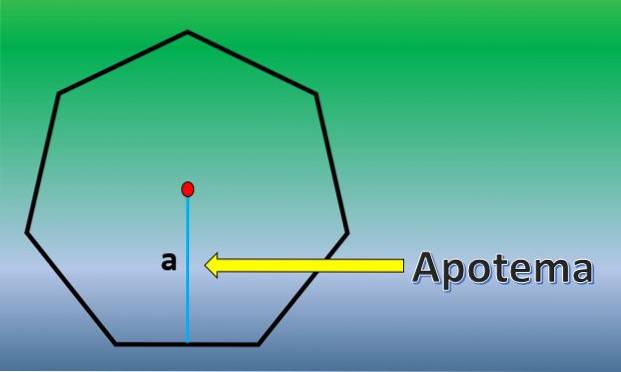
När apotemet är känt är heptagons område H = 7xLxa / 2, där "L" är längden på varje sida och "a" är längden på apotemet..

Arean för ett parallellogram är lätt att beräkna, det definieras som P = Lxh, där "L" har samma längd som sidan av heptagon och "h" är prismahöjden.

Sammanfattningsvis är mängden material som behövs för att bygga ett heptagonalt prisma (med vanliga baser) 7xLxa + 7xLxh, det vill säga 7xL (a + h).

4- Volym

När väl basytan och prismahöjden är känd, definieras volymen som (area av basen) x (höjd).

I fallet med ett heptagonalt prisma (med vanlig bas) är dess volym V = 7xLxaxh / 2; det kan också skrivas som V = Pxaxh / 2, där "P" är omkretsen av det vanliga heptagonen.

Referenser

1. Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematik: En problemlösning för grundskolelärare. López Mateos Redaktörer.
2. Fregoso, R. S. och Carrera, S. A. (2005). Matematik 3. Redaktionellt Progreso.
3. Gallardo, G., och Pilar, P. M. (2005). Matematik 6. Redaktionellt Progreso.
4. Gutiérrez, C. T. och Cisneros, M. P. (2005). Matematikkurs 3. Redaktionellt Progreso.
5. Kinsey, L. och Moore, T. E. (2006). Symmetri, form och rymd: En introduktion till matematik genom geometri (illustrerad, omtryckt red.). Springer Science & Business Media.
6. Mitchell, C. (1999). Bländande Math Line Designs (Illustrerad utgåva). Scholastic Inc..
7. R., M. P. (2005). Jag drar 6: e. Redaktionellt Progreso.