De villkorlig sannolikhet Det är möjligheten att en viss händelse inträffar, med tanke på att en annan inträffar som ett tillstånd. Denna ytterligare information kan (eller kanske inte) modifiera uppfattningen att något kommer att hända.
Vi kan till exempel fråga oss själva: "Vad är sannolikheten för att det regnar idag, med tanke på att det inte har regnat på två dagar?" Den händelse som vi vill veta sannolikheten för är att det regnar idag, och den ytterligare informationen som villkorar svaret är att "det har inte regnat på två dagar".
Var en probabilistiskt utrymme sammansatt av Ω (samplingsutrymme), ℬ (slumpmässiga händelser) och P (sannolikheten för varje händelse), plus händelserna A och B som tillhör ℬ.
Den villkorliga sannolikheten för att A inträffar, med tanke på att B inträffade, vilket betecknas som P (A│B), definieras enligt följande:
P (A│B) = P (A∩B) / P (B) = P (A och B) / P (B)
Där: P (A) är sannolikheten för förekomst av A, P (B) är sannolikheten för händelse B och skiljer sig från 0, och P (A∩B) är sannolikheten för skärningspunkten mellan A och B, det vill säga ,, sannolikheten för att båda händelserna inträffar (gemensam sannolikhet).
Detta är ett uttryck för Bayes sats tillämpad på två händelser, som föreslogs 1763 av den engelska teologen och matematikern Thomas Bayes.
Artikelindex
-Varje villkorlig sannolikhet är mellan 0 och 1:
0 ≤ P (A│B) ≤ 1
-Sannolikheten att händelse A inträffar, med tanke på att händelse inträffar, är uppenbarligen 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Om två händelser är exklusiva, det vill säga händelser som inte kan hända samtidigt, är den villkorliga sannolikheten att en av dem händer 0, eftersom korsningen är noll:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Om B är en delmängd av A, är den villkorliga sannolikheten också 1:
P (B│A) = P (A∩B) / P (A) = 1
Viktig
P (A│B) är i allmänhet inte lika med P (B│A), därför måste vi vara försiktiga med att inte byta händelser när vi hittar den villkorliga sannolikheten.
Många gånger vill du hitta den gemensamma sannolikheten P (A∩B) snarare än den villkorliga sannolikheten. Sedan har vi genom följande sats:
P (A∩B) = P (A och B) = P (A│B). P (B)
Satsen kan utvidgas till tre händelser A, B och C:
P (A2B2C) = P (A och B och C) = P (A) P (B2A) P (C2A2B)
Och även för olika evenemang, som A1, TILLtvå, TILL3 och mer kan det uttryckas enligt följande:
P (A1∩ Atvå ∩ A3... ∩ An) = P (A.1). P (Atvå│A1). P (A3│A1∩ Atvå) ... P (An││A1∩ Atvå∩ ... An-1)
När det är fallet med händelser som inträffar i följd och genom olika steg är det bekvämt att organisera data i ett diagram eller en tabell. Detta gör det lättare att visualisera alternativen för att nå önskad sannolikhet..
Exempel på detta är träddiagram och den beredskapstabell. Från en av dem kan du bygga den andra.
Låt oss titta på några situationer där sannolikheten för en händelse ändras av förekomsten av en annan:
Två sorters kakor säljs i en söt butik: jordgubbe och choklad. Genom att registrera preferenser för 50 klienter av båda könen bestämdes följande värden:
-27 kvinnor, varav 11 föredrar jordgubbstårta och 16 chokladkaka.
-23 män: 15 väljer choklad och 8 jordgubbar.
Sannolikheten att en kund väljer en chokladkaka kan bestämmas genom att tillämpa Laplaces regel, enligt vilken sannolikheten för varje händelse är:
P = antal gynnsamma händelser / totalt antal händelser
I det här fallet av totalt 50 kunder föredrar totalt 31 choklad, så sannolikheten skulle vara P = 31/50 = 0,62. Det vill säga 62% av kunderna föredrar chokladkaka.
Men skulle det vara annorlunda om klienten är en kvinna? Detta är ett fall av villkorlig sannolikhet.
Med hjälp av en beredskapstabell som denna visas totalen enkelt:
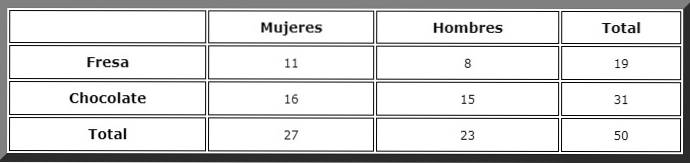
Sedan observeras de gynnsamma fallen och Laplaces regel tillämpas, men först definierar vi händelserna:
-B är händelsen "kvinnlig klient".
-A är händelsen "föredrar chokladkaka" att vara kvinna.
Vi går till kolumnen "kvinnor" och där ser vi att summan är 27.
Då söks det gynnsamma fallet i raden "choklad". Det finns 16 av dessa händelser, därför är sannolikheten direkt:
P (A│B) = 16/27 = 0,5924
59,24% av de kvinnliga kunderna föredrar chokladkaka.
Detta värde sammanfaller när vi kontrasterar det med den ursprungligen angivna definitionen av villkorlig sannolikhet:
P (A│B) = P (A∩B) / P (B)
Vi ser till att använda Laplaces regel och värdena i tabellen:
P (B) = 27/50
P (A och B) = 16/50
Där P (A och B) är sannolikheten för att kunden föredrar choklad och är en kvinna. Nu är värdena ersatta:
P (A│B) = P (A och B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
Och det är bevisat att resultatet är detsamma.
I detta exempel gäller multiplikationsregeln. Anta att det finns byxor i tre storlekar som visas i en butik: små, medelstora och stora..
I en massa med totalt 24 byxor, av vilka det finns 8 av varje storlek och alla är blandade, vad skulle vara sannolikheten att extrahera två av dem och att båda var små?
Det är tydligt att sannolikheten för att ta bort en liten byxa vid första försöket är 8/24 = 1/3. Nu är den andra extraktionen konditionerad till den första händelsen, eftersom när man tar bort ett par byxor finns det inte längre 24 utan 23. Och om en liten byxa tas bort finns det 7 istället för 8.
Händelse A drar en liten byxa, efter att ha dragit en annan vid första försöket. Och händelse B är den med de små byxorna första gången. Därför:
P (B) = 1/3; P (A│B) = 7/24
Slutligen med multiplikationsregeln:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
I en studie av punktlighet på kommersiella flygflygningar finns följande uppgifter tillgängliga:
-P (B) = 0,83, är sannolikheten för att ett plan lyfter i tid.
-P (A) = 0,81, är sannolikheten att landa i tid.
-P (B∩A) = 0,78 är sannolikheten för att flyget anländer i tid och tar fart i tid.
Det ombeds att beräkna:
a) Vad är sannolikheten för att planet kommer att landa i tid med tanke på att det startade i tid?
b) Är den tidigare sannolikheten densamma som sannolikheten att han lämnade i tid om han lyckades landa i tid??
c) Och slutligen: vad är sannolikheten att den kommer fram i tid med tanke på det inte kom ut i tid?
För att besvara frågan används definitionen av villkorlig sannolikhet:
P (A│B) = P (A∩B) / P (B) = P (A och B) / P (B) = 0,78 / 0,83 = 0,9398
I det här fallet utbyts händelserna i definitionen:
P (B│A) = P (A∩B) / P (A) = P (A och B) / P (A) = 0,78 / 0,81 = 0,9630
Observera att denna sannolikhet skiljer sig något från den tidigare, som vi tidigare påpekade.
Sannolikheten att inte lämna i tid är 1 - P (B) = 1 - 0,83 = 0,17, vi kommer att kalla det P (BC), eftersom det är den kompletterande händelsen att ta fart i tid. Den villkorliga sannolikheten som eftersträvas är:
P (A│BC) = P (A∩BC) / P (BC) = P (A och B.C) / P (BC)
Å andra sidan:
P (A∩BC) = P (landning i tid) - P (landning i tid och start i tid) = 0,81-0,78 = 0,03
I detta fall är den villkorliga sannolikheten som eftersträvas:
P (A│BC) = 0,03 / 0,17 = 0,1765
Ingen har kommenterat den här artikeln än.